Соотношение (8) позволяет сделать важный вывод о том, что общая случайная погрешность 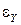 есть линейная функция погрешностей отдельных аргументов
есть линейная функция погрешностей отдельных аргументов 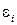
Применяя известную теорему о дисперсии линейной функции случайных аргументов, получим выражение для СКО результирующей случайной погрешности:
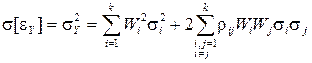 =
=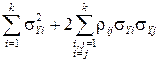 , (10)
, (10)
где 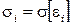 и
и 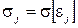 — СКО случайных погрешностей i -го и j -го аргументов;
— СКО случайных погрешностей i -го и j -го аргументов; 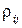 - коэффициент корреляции между каждой парой аргументов
- коэффициент корреляции между каждой парой аргументов 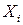 ,
, 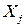 :
:
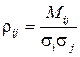 , (11)
, (11)
где 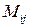 -корреляционный момент. При этом
-корреляционный момент. При этом 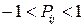 (корреляция может быть положительной или отрицательной)
(корреляция может быть положительной или отрицательной)
Рассмотрим несколько важных частных случаев:
1. Все аргументы 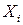 независимы. В этом случае все
независимы. В этом случае все 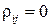 и
и
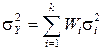 =
=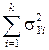 (12)
(12)
2. Функция Y есть линейная функция независимых аргументов 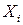 , т. е.
, т. е.
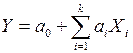 (13)
(13)
где 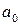 ,
, 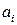 — постоянные коэффициенты
— постоянные коэффициенты
Для этого случая СКО результирующей погрешности, очевидно, определится соотношением:
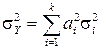 (14)
(14)
3. Величина Y определяется произведением степеней независимых аргументов:
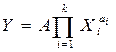 (15)
(15)
где А – постоянный сомножитель. Применяя к этому случаю соотношение (12) и представляя относительные СКО (ОСКО) в виде 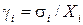 ,
, 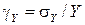 , нетрудно получить аналогичное (14) выражение для ОСКО результирующей погрешности:
, нетрудно получить аналогичное (14) выражение для ОСКО результирующей погрешности:
|
|
|
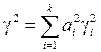 (16)
(16)
4. Суммирование двух случайных погрешностей (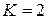 ). При этом
). При этом
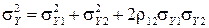 (17)
(17)
Отметим, что выражение (17) имеет полную аналогию с известной формулой для диагонали параллелограмма, если считать 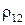 косинусом угла между смежными сторонами
косинусом угла между смежными сторонами 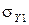 и
и 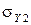 . Поэтому говорят, что СКО составляющих случайных погрешностей складываются геометрически. В частности, если
. Поэтому говорят, что СКО составляющих случайных погрешностей складываются геометрически. В частности, если 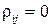 , то
, то
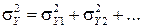 , (18)
, (18)
т. е. складываются квадраты СКО — дисперсии. А когда 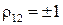 , т.е. когда существует функциональная связь между
, т.е. когда существует функциональная связь между 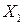 и
и 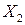 , алгебраически складываются первые степени СКО:
, алгебраически складываются первые степени СКО:
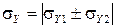 (19)
(19)
Граничные значения 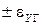 общей погрешности, как известно, можно найти, умножая
общей погрешности, как известно, можно найти, умножая 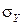 на коэффициент
на коэффициент 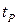 , зависящий от закона распределения
, зависящий от закона распределения 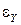 :
: 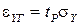 . Для этого надо уметь определять плотность распределения
. Для этого надо уметь определять плотность распределения 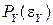 .
.
 2014-02-18
2014-02-18 1555
1555