Метод Гаусса. Матричный метод. Формулы Крамера

Матричный метод. Формулы Крамера

Рассмотрим квадратную (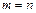), невырожденную (________)СЛАУ

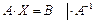слева.

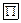
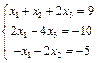
Из системы 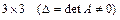найдем в общем виде, например, . Здесь

.

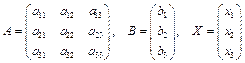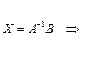
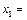
Это равенство можно записать в виде 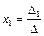, где обозначено

.

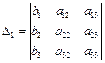Вообще, при для решений СЛАУ справедливы ф-лы Крамера:

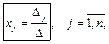
где – _______________________________________,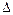

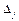получается из _________________________________________________.

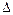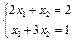
Один из наиболее универсальных и эффективных методов (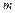не обязательно равно 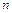, а в случае 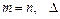не обязательно ).

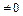I. Прямой ход. Элементарными преобразованиями над строками приводим расширенную матрицу системы к «треугольному» виду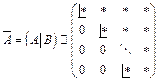

II. Обратный ход. Решаем эквивалентную систему, восстановленную по последней матрице «снизу вверх».

1.

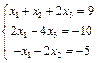
2.

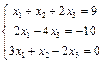
Действительно, здесь .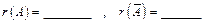

3.

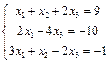
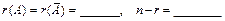(, т.е. 1 свободная, 2 базисных неизвестных).

Замечание. Однородная система, т.е. (4), где 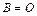, всегда совместна. Она имеет как минимум одно решение ________, так называемое тривиальное решение.

Бесконечное множество решений – если 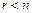. В частности, пр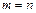и и – однородная СЛАУ имеет нетривиальные решения.

ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ