Лекция № 9 Классификация функций выбора

Задача векторной оптимизации

Классификация функций выбора

Обозначим S - множество всех возможных функций выбора. Простейшая классификация различает следующие подмножества S:

а) S _>0 - подмножество функций непустого выбора, т.е. таких

функций, выбор по которым содержит хотя бы один элемент.

б) S₁ - подмножество функций однозначного выбора, т.е. таких функций, выбор по которым содержит ровно один элемент.

Ясно, что S₁ Í S _>0 Í S.

Приведем без доказательства следующие теоремы о функциях выбора.

ТЕОРЕМА 1. Бинарное отношение R порождает функцию непустого выбора, основанную на механизме доминирования или блокировки тогда и только тогда, когда R ациклично.

ТЕОРЕМА 2. Бинарное отношение R порождает функцию однозначного выбора, основанную на механизме доминирования или блокировки тогда и только тогда, когда R ациклично и слабополно.

Более тонкая классификация функций выбора основывается на наличии или отсутствии у них следующих свойств.

1) H: (YÍX) => C(X)ÇYÍC(Y) - свойство наследования.

Наличие этого свойства означает, что элемент b, выбираемый на множестве Х, будет также выбран на любом более узком содержащем его подмножестве Y. Иными словами, при переходе к рассмотрению элемента b на более узком множестве, его свойство быть выбранным сохраняется (наследуется).

2) C: X = YÈZ => (C(Y)ÇC(Z))ÌC(X) - свойство согласия.

Наличие этого свойства означает, что элемент b, выбираемый одновременно на любых составных частях некоторого множества Х, будет также выбран на всем Х.

3) О: (C(X)ÍYÍX) => (C(Y) = C(X)) - свойство отбрасыва-

ния или независимости от отбрасывания отвергнутых вариантов. Оно означает, что выбор на любом множестве Y, содержащем выбор C(X) совпадает с C(X). Т.е. выбор не зависит от того, сколько "плохих" элементов пришлось отбросить при выборе.

4) K: (YÍX) => (C(Y) = YÇ(X)) - свойство строгого нас-

ледования (константности).

Перечислим ряд закономерностей, которые вытекают из названных свойств функций выбора.

Пусть (H), (C), (O), (K) Ì S - множества функций выбора,

удовлетворяющих соответствующим свойствам.

ТЕОРЕМА 3. (K)Ì(H)Ç(C)Ç(O). Т.е. если функция выбора

обладает свойством K, то она обладает одновременно свойствами H, C, O.

ТЕОРЕМА 4. Для того чтобы функции выбора порождалась бинарным отношением R посредством механизма доминирования или блокировки, необходимо и достаточно, чтобы она принадлежала области (H)Ç(С).

ТЕОРЕМА 5. Для того чтобы функция выбора порождалась качественным порядком необходимо и достаточно, чтобы она принадлежала области (H)Ç(С)Ç(O).

ТЕОРЕМА 6. Для того чтобы функция выбора порождалась слабым порядком необходимо и достаточно, чтобы она принадлежала области (К).

Свойства Н, С, О кажутся очень естественными при выборе. Тем не менее, несложно привести пример, когда эти свойства не выполняются.

Пусть Х - множество точек на плоскости ограниченных прямоугольником АBCD: A(0,0), B(0,4), C(2,4), D(2,0)

Ставится следующая задача выбора: на множестве Х найти геометрическое место центров кругов, включенных в Х, максимального радиуса. Покажем что соответствующая функция выбора не обладает ни одним из свойств H, K, O, C.

1) Пусть Х = АBCD; Y = АEFD; E(0,2), F(2,2) (Рис. 1). Тогда

множеством центров кругов максимального радиуса, вписанных в ABCD, яввляется отрезок PQ (C(X)=PQ), где P(1,3), Q(1,1). Тогда C(X)ÇY = QR. Очевидно, что C(Y)=Q. Получили, что на множестве X нашлось такое подмножество Y, что хотя

YÌX, тем не менее множество YÇC(Х) не включено в C(Y), т.е нарушаются условия H и K.

2) Пусть Y = MNOT: M(0,1), N(0,3), O(2,3), T(2,1) (Рис. 2).

Так как, по прежнему, C(X) = PQ, а C(Y)=R(3,3), то

C(X)ÌYÌX.Равенство C(X)=C(Y) при этом не выполняется, т.е нарушается условие O.

В классических задачах оптимизации необходимо найти минимум или максимум скалярной функции - функции цели или критерия эффективности. Но в практических задачах редко удается свести эффективность к одному показателю.

Пример. Пусть необходимо сконструировать самолет. Основными, одинаково важными, критериями эффективности конструкции являются скорость и дальность полета. Увеличивая дальность полета самолета, мы уменьшаем его скорость и наоборот. Такая ситуация называется конфликтом критериев.

В том случае, когда имеется несколько конфликтующих критериев, говорят, что имеет место задача векторной оптимизации.

F(x) = { f ₁(x), f ₂(x),..., f _n(x) } ® орt,

где f _i- частные критерии эффективности.

Как правило, не существует такой точки в которой все f _i оптимальны. Поэтому в задаче векторной оптимизации ищут компромиссное решение. Для эффективного поиска такого решения необходимо, чтобы число возможных допустимых вариантов было как можно меньше.

Для достижения такой цели задачу разбивают на 2 этапа.

1) Поиск нехудших (недоминируемых) решений в смысле безусловного критерия предпочтения (БКП). Множество таких точек называется множеством Парето.

2) Выбор компромиссного решения на множестве Парето.

Рассмотрим пример [6]. Пусть имеем два критерия эффективности q₁(x) и q₂(x), зависящих от одного аргумента х, каждый из которых необходимо минимизировать (Рис.3).

Обозначим Х₁ и Х₂ - точки минимума критериев q₁(x) и q₂(x),

соответственно. Разобьем область определения аргумента х на три участка: I, II, III. Осуществим на каждом участке выбор точек, лучших по Парето, т.е. по обоим критериям одновременно:

а) C_par(I) = Х₁ - выбор на I участке есть точка X₁;

б) C_par(III) = X₂ - выбор на III участке есть точка X₂;

в) на участке II нет точки, которая была бы лучше остальных

сразу по обоим критериям, т.е. он весь состоит из конфликтующих точек, следовательно, C_par(II)=[X₁, X₂].

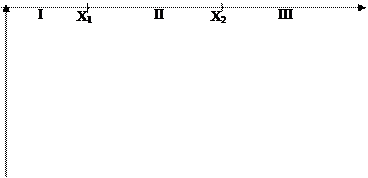Рис. 3

Чтобы найти множество Парето в общем случае надо реализовать функцию выбора на основе паретовского механизма (механизма блокировки в смысле бинарного отношения Парето) (см. п.6). Для того чтобы построить эту функцию достаточно организовать сравнение предлагаемых вариантов по каждой критериальной функции. Для этой задачи можно достаточно легко построить алгоритм решения, т.е она формализуема.

Для задачи второго этапа необходимо применять неформальные методы выбора, основанные на интуитивных предпочтениях эксперта или лица принимающего решения (ЛПР).

Для организации паретовского механизма выбора необходимо произвести парные сравнения исходных вариантов и отбросить те, для которых найдется доминирующий элемент. Если исходное множество велико, то метод попарного сравнения трудоемок, т.к в общем случае необходимо произвести m(m-1)/2 сравнений, где m – число сравниваемых вариантов.

Более эффективен следующий алгоритм, который производит последовательное накопление элементов искомого множества.

Обозначим X = {x_i} - исходное множество сравниваемых вариантов. Для него будем производить отсев плохих точек и получение множества П(Х), содержащее точки Парето.

begin П(Х):={х₁};

for i:=2 to m do

П(Х):=C_par ({x_i} È П(Х));

end.

При реализации этого алгоритма возможны три случая:

1) Для х_i существует такой у Î П(Х), что у Par x_i. В этом случае необходимо прекратить сравнение х_i с паретовскими точками и перейти к х_i+1.

2) Для х_i существует такой у Î П(Х), что x_i Par у. В этом

случае необходимо исключить y из П(Х) и продолжить сравнение х_i с оставшимися точками пока не будет просмотрено все текущее множество П(Х). Если процесс сравнения не прекратился раньше, чем было просмотрено все П(X), то х_i необходимо включить в П(Х).

3) Для х_i не существует такого у Î П(Х), чтобы у Par x_i или x_i Par у. В этом случае y не исключают и продолжают сравнение х_i с оставшимися точками также, как и в случае 2).

Обычно множество недоминируемых точек содержит значительно меньше элементов, чем исходное т.е k = |П(Х)|<<|Х| = m. В этом случае нужно провести O(m×k) сравнений, т.е. значительно меньше, чем при всевозможных парных сравнениях.

Данный алгоритм даст верное решение, если для любых множеств X и Y выполняется условие:

C^R(X È Y) = C^R(X È C^R(Y)) (1)

ТЕОРЕМА. Соотношение (1) выполняется, если функция выбора обладает свойствами Н и О.

ДОКАЗАТЕЛЬСТВО. Вспомним свойства

- наследования: (Y Í X) => C(X) Ç Y Í C(Y);

- отбрасывания: (C(X) Í Y Í X) => (C(Y) = C(X)).

Покажем, что при их выполнении C^R(XÈY) Í XÈC^R(Y).

Пусть х Î C^R(XÈY). Если х Î X, то х Î XÈC^R(XÈY). Пусть теперь х Î Y, тогда х Î C^R(XÈY)ÇY. В силу свойства наследования получим, что Y Í XÈY, поэтому C^R(XÈY)ÇYÍ C ^R(Y). Значит, x Î C^R(Y), а, следовательно, x Î XÈC^R(Y), что доказывает

утверждение.

Обозначим A = XÈY, B = XÈC^R(Y). По доказанному ранее C^R(XÈY) Í XÈC^R(Y) Í XÈY. Тогда по свойству отбрасывания C^R(A) = C^R(B) или С^R(XÈY) = С^R(XÈС^R(Y)), что и требовалось доказать.

Условие (1) в частности выполняется, если R – качественный порядок (см. п.11, ТЕОРЕМА 5). T.к отношение Парето таковым является, то алгоритм позволяет построить искомое конфликтное множество.