Производящие функции

4.1. Определение производящих функций. Последовательности {u_n}, фигурирующей в какой-либо задаче, например, комбинаторной, удобно поставить в соответствие формальный степенной ряд

u(x) = ,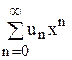

который называется производящей функцией данной последовательности. Слова “формальный ряд” означает, что эту формулу мы трактуем только как удобную запись последовательности. Для нас сейчас несущественно, при каких значениях х ряд сходится и сходится ли вообще, т.к. вычислять значение u(x) мы никогда не будем.

Пример 3.5. Известно, что 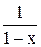= 1 + х + х² + … + хⁿ + … Следовательно, функция 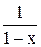является производящей для последовательности 1,…, 1.

Пример 3.6. Согласно формуле бинома Ньютона (1 + х)ⁿ = 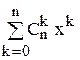. Следовательно, функция (1 + х)ⁿ является производящей для конечной последовательности .

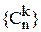4.2. Операции с производящими функциями. Рассмотрим основные технические приемы, применяемые в работе с производящими функциями.

4.2.а. Линейная комбинация. Если функция u(x) соответствует последовательности {u_n}, а v(x) – последовательности {v_n}, то функция a×u(x) + b×v(x) (a и b – константы) является производящей для последовательности { a×u_n + b×v_n}.

4.2.б. Сдвиг. Если функция u(x) соответствует последовательности {u_n}, то функции х^m×u(x) соответствует последовательность 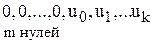… – сдвиг вправо.

Аналогично, функция 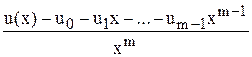является производящей для последовательности u_m, u_m+1, … – сдвиг влево.

4.2.в. Умножение. Если функция u(x) соответствует последовательности {u_n}, а v(x) – последовательности {v_n}, то функции u(x)×v(x) соответствует последовательность {w_n}, где

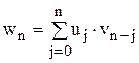– формула Коши. Например, w₀ = u₀×v₀; w₁ = u₀ ×v₁ + u₁ ×v₀; w₂ = u₀ ×v₂ + u₁ ×v₁ + u₂ ×v₀.

Пример 3.7. Пусть u(x) соответствует последовательности {u_n}, а v(x) = 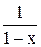– производящая функция для последовательности 1,…, 1 (см. пример 3.5). Тогда функция

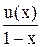= u₀ + (u₀ + u₁) x + (u₀ + u₁ + u₂) x² +… (3.9)

является производящей для последовательности частичных сумм.

4.2.г. Дифференцирование и интегрирование. Если u(x) соответствует последовательности {u_n}, то по правилу дифференцирования рядов

u¢(x) = 0 + u₁ + 2 u₂ x + 3 u₃ x² + ….

То есть u¢(x) является производящей функцией для последовательности {k u_k}.

Аналогично 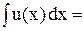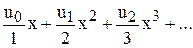. То есть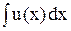является производящей функцией для последовательности .

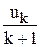Пример 3.8. 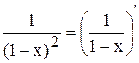= 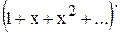. Следовательно, функция 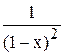является производящей для последовательности {k}.

Далее,

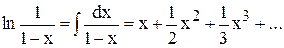(3.10)

Следовательно, 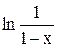является производящей функцией для последовательности .

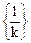Сопоставляя (3.10) с (3.9) получаем

,

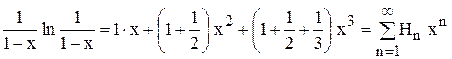где 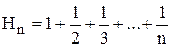– гармонические числа.

4.3. Пример использования производящих функций

Решим с помощью производящих функций следующую комбинаторную задачу.

Пример 3.9. На окружности находится 2n точек. Сколькими способами можно их попарно соединить так, чтобы полученные отрезки не соединялись друг с другом?

Решение. Обозначим u_n – число способов соединить 2n точек. Построим рекуррентное соотношение.

Формально положим u₀ = 1 (нет точек, нет пересечений, следовательно, способ единственный). u₁ = 1 – очевидно, т.к. две точки соединяются единственным способом, и пересечений нет. u₂ = 2. Способы соединения изображены на рис. 3.1.

		Рис. 3.1. Способы соединения 4-х точек

Пусть n > 1. Выберем одну из 2(n + 1) точек, обозначим ее А. Соединим А с вершиной В, выбрав ее так, чтобы с обеих сторон от соединяющей их линии находилось четное число точек. Пусть слева будет 2k точек, справа – 2(n – k). 2k точек можно соединить между собой u_k способами, 2(n – k) точек – u_n–k способами. При этом линии не пересекутся, т.к. 2k и 2(n – k) точек расположены по разные сторона от АВ.

Следовательно, при фиксированном k получим u_k×u_n–k способов соединения. Но k меняется от 0 до n. Следовательно,

u_{n +1} = u₀×u_n + u₁×u_n–1 + … + u_n×u₀. (3.11)

Получили искомое нелинейное рекуррентное соотношение, формула общего решения которого нам, к сожалению, неизвестна.

Чтобы получить явную формулу для u_n, построим для этой последовательности производящую функцию.

u(x) = u₀ + u₁х + u₂ x² + u₃ x³ + …. (3.12)

Имеем, согласно формуле Коши:

[ u(x) ]² = (u₀)² + (u₀×u₁ + u₁×u₀) х + (u₀×u₂ + u₁×u₁ + u₂×u₀)х² + …

Видно, что коэффициенты для разложения [ u(x) ]² можно получить с помощью формулы (3.11).

Из (3.12) имеем: 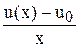= u₁ + u₂ x + u₃ x² + ….

Подставим в эту формулу выражение u_k согласно (3.11). С учетом того, что u₁ = (u₀)² получим: 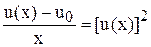. Следовательно, имеем квадратное уравнение относительно u(х). Решив его, получим .

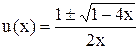По формуле бинома имеем:

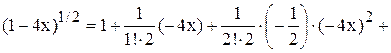
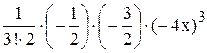++…= 1 –.

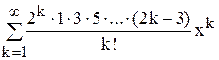Умножим каждое k-е слагаемое на 1 = 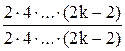. Тогда коэффициент k-го члена ряда равен:

= = = .

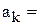
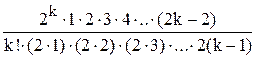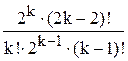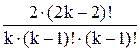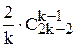Отсюда

.

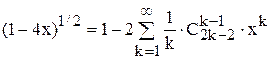Для того, чтобы коэффициенты ряда были положительными, надо перед корнем в формуле u(x) брать знак “–”. Заменим индекс суммирования k на k +1. В результате получим:

u(x) = == .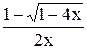

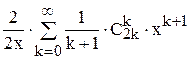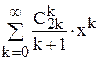Окончательно 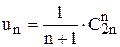– это так называемые, числа Каталана.