| |||||||||
 | |||||||||
 | |||||||||
| |||||||||
| |||||||||
Свойства графов легко связать со свойствами соответствующих бинарных отношений, т.к. R и E означают одно и то же. Например:
R – симметрично Þ G – неориентированный;
R – асимметрично Þ G – ориентированный, без петель;
R – антисимметрично Þ G – ориентированный, с неориентированными петлями;
R – рефлексивно Þ G имеет петли;
отношению R–1 соответствует граф с обратной ориентацией дуг;
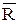 соответствует
соответствует 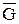 и т.д.
и т.д.
Изоморфизм. При изображении графа в виде точек с линиями такие понятия, как длина или кривизна линий не важны. Главное – изобразить, какие именно пара вершин соединяет данное ребро. Например, на рис. Графы а) и б) одинаковы, а а) и в) совпадают с точностью до нумерации вершин и ребер.

Такие графы называются изоморфными. Более строго:
Def. Пусть G = (V, E), H = (U, F) – графы. Пусть f: V «U – взаимно-однозначное отображение. Если для любых v, w Î V их образы f(v) и f(w) смежны тогда и только тогда, когда смежны v и w, то f называется изоморфизмом G на H, а сами графы – изоморфными (обозначается G ~ H). Если f – тождественное отображение, то G = H.
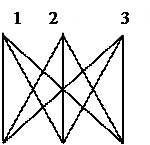
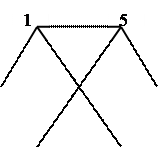
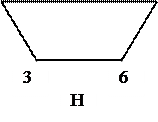
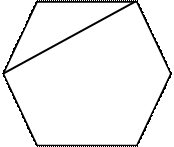
Пример 1.2. G ~ H ~ I, а J и K не изоморфны.
 | |||||
 |  | ||||

 | |||||||||||||
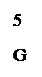 | |||||||||||||
| |||||||||||||
 |  | ||||||
|
|
 2014-02-18
2014-02-18 473
473