Теоремы о вершинных подмножествах

Определения вершинных подмножеств

Специальные вершинные подмножества графа

На основе понятий смежности, связности и достижимости на графах определяют специальные подмножества вершин.

База – минимальное множество В вершин, из которых достижима любая вершина графа. База обладает следующими свойствами.

1) Каждая вершина графа достижима хотя бы из одной вершины множества В

2) В множестве В нет вершин, которая достижима из другой вершины множества В.

Доминирующее множество (внешне устойчивое множество) графа – такое множество S вершин, что любая вершина из V\S смежна с какой-нибудь вершиной из S. Иными словами " uÎV\S $ vÎS: (v, u) ÎE. Доминирующее множество называется минимальным, если его подмножество уже не является доминирующим.

Независимое множество (внутренне устойчивое множество) графа – множество N несмежных вершин. То есть " u, v Î N (u, v)ÏE. N называется максимальным независимым множеством, если любое множество H, включающее в себя N, уже не является независимым.

Вершинное покрытие. Говорят, что вершина покрывает инцидентное ей ребро. Множество U таких вершин, которые покрывают все ребра графа, называется вершинным покрытием графа. Вершинное покрытие минимальной мощности называется минимальным вершинным покрытием.

Клика (максимально полный подграф) – множество вершин К, такое, что построенный на нем подграф является полным и для любого множества H, включающего в себя К, построенный на нем подграф уже не является полным.

а) База – т.к. граф связный, то любая вершина может быть базой.

б) Доминирующие множества – {8, 7, 2, 5}, {7, 5, 1}, {1, 4}, {4, 6}. Два последних – минимальные доминирующие множества.

в) Максимальные независимые множества – {8, 7, 2, 5}, {7, 5, 1}, {1, 4}. А {2, 7, 5} независимое, но не максимальное, т.к. включено в {8, 7, 2, 5}.

г) Вершинные покрытия – {6, 3, 1, 4}, {8, 3, 2, 4, 1}, {1, 2, 3, 4, 5, 6, 7, 8}. Минимальное вершинное покрытие – {6, 3, 1, 4} мощности 4.

д) Клики – {1, 2, 6}, {1, 6, 8}, {3, 4, 5}. А {1, 2, 6, 8} – не клика, т.к. нет ребра (2, 8).

Теорема 5.1. (о независимости и доминировании). Независимое множество вершин максимально тогда и только тогда, когда является доминирующим.

Доказательство. Необходимость. Пусть N – максимальное независимое множество. Предположим противное, что оно не доминирующее. Это значит, что есть вершина v, несмежная ни с одной вершиной из N. Тогда v можно добавить к N с сохранением у N независимости. Это противоречит тому, что N – максимальное.

Достаточность. Пусть N – независимое доминирующее множество. Предположим противное, что оно не максимальное. Это значит, что есть вершина v, несмежная ни с одной вершиной из N. Это противоречит тому, что N – доминирующее.

Теорема 5.2. (об эквивалентности вершинных множеств). Для любого неориентированного графа G = (V, E) и подмножества WÍV следующие утверждения эквивалентны.

1) W – вершинное покрытие графа G.

2) V \ W – независимое множество графа G.

3) V \ W – клика в графе .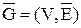

Доказательство. 1) Þ 2). Пусть W – вершинное покрытие. Возьмем любое ребро (u, v) ÎE. Тогда, по определению вершинного покрытия, либо u ÎW, либо v ÎW. То есть u и v не могут одновременно принадлежать V \ W. Значит, если одновременно u ÎV \ W и v Î V \ W, то (u, v) ÏE. Это означает, что V \ W – независимое множество.

2) Þ 3). Пусть U Í V – какое-нибудь независимое множество. Значит для любой пары вершин u, v ÎU будет (u, v) ÏE или 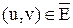. Следовательно, U – клика в графе 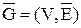. Обозначим W = V \ U, тогда U = V \ W – получим нужное следствие.

3) Þ 1). Пусть U – клика в графе 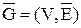. Значит для любой пары вершин u, v ÎU будет (u, v) ÏE. Это значит, что если (u, v) ÎE, то или u ÏU либо v ÏU. Другими словами из (u, v) ÎE следует, что либо u ÎV \ U, либо v ÎV \ U. Следовательно, V \ U – вершинное покрытие G. Обозначим W = V \ U (т.е. U = V \ W), получим, что если V \ W – клика в графе 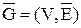, то W – вершинное покрытие.