Лекция № 16 Машинная реализация алгоритма Краскала

Остов

Def. Пусть G = (V, E) – неориентированный граф с n вершинами. Остовным деревом (остовом) графа G называется дерево T = (V, E₁), E₁ Í E.

Остов можно построить с помощью алгоритма поиска любого вида (в глубину и в ширину). Для этого во время поиска в G параллельно строится новый граф Т: если найдена новая еще непомеченная вершина uв списке инцидентности вершины v, то ребро (v, u) добавляется в строящийся граф. Если исходный граф несвязный, то задача не имеет решения.

Для связного исходного графа получим, что построенный граф является связным, так как новые ребра достраиваются к уже просмотренным вершинам, которые между собой достижимы. Этот граф не содержит циклов, так как в него не добавляется ребро, оба конца которого просмотрены, т.е. связаны маршрутом. Следовательно, построенный граф является деревом.

Задача построения остова имеет большое прикладное значение. Она возникает при прокладке трасс и сетей коммуникаций, которые должны связать n заданных точек. Обычно требуют, чтобы остов обладал некоторым оптимальным свойством. Например, если каждое ребро имеет некоторый вес, то остов должен иметь минимальный вес.

Алгоритм Краскала. Этот алгоритм применяется для построения остова минимального веса. Пусть имеем граф G = (V, E), в котором каждому ребру присвоен вес r(e) – некоторое вещественное число. Основная идея алгоритма: начиная с полностью несвязного графа Т = (V, Æ), присоединяем к нему ребра графа G в порядке возрастания их веса; если после присоединения очередного ребра в Т может образоваться цикл, то это ребро не присоединяем, а переходим к следующему. Можно доказать, что таким образом строится остов минимального веса.

Машинная реализация алгоритма Краскала. Сложность машинной реализации заключается в следующем.

1). Перед выполнением необходимо, чтобы ребра графа были отсортированы в порядке возрастания веса. Эта операция имеет сложность О(m²), а если граф близок к полному, то О(n⁴) – достаточно высокая.

2). Существенным моментом алгоритма является проверка на наличие цикла при добавлении ребра. В любом графе при добавлении ребра цикл появляется, если только присоединяемые ребра принадлежат одной компоненте связности. Следовательно, для контроля образования цикла необходимо каждой вершине приписать номер ее компоненты связности и следить, чтобы номера компонент двух соединяемых вершин всегда различались. После соединения вершин их компоненты связности сольются в одну, значит, надо соответствующим образом поменять их номера.

Алгоритм.

begin T:= Æ; for i:=1 to n do КОМП[i]:= i;

for j:=1 to m do

begin a:=НАЧАЛО[e[j]];

b:=КОНЕЦ[e[j]];

if КОМП[a] <> КОМП[b] then

begin Т:= T;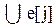

for i:=1 to n do

if КОМП[i] = КОМП[b] then

КОМП[i]:= КОМП[a];

end;

end;

end. Оценим вычислительную сложность без сортировки. Просмотр списка ребер – O(m) операций. Внутренний цикл по i от 1 до n – повторяется n – 1 раз, по числу добавляемых ребер. Итого О(m) + О(n²) = О(n²).