Развитие методов решения нелинейных дифференциальных уравнений

В рассматриваемый период развития теории колебаний большинство задач решалось с помощью линеаризации и в течение XVIII–XIX веков теория малых, линейных колебаний была развита достаточно хорошо. В то время понятие малости колебаний отождествлялось с линейностью модели, хотя на самом деле это не всегда выполняется, например, для нелинейностей типа «зазор» или «натяг». Даже слабая нелинейность порой приводит к эффектам, которые не могут быть объяснены в линейной постановке.

Нелинейность механических систем проявляется в случаях, когда упругая восстанавливающая сила нелинейно зависит от смеще­ния точек системы от положения равновесия. Иногда это связано с характерис­тиками применяемых материалов, например, резина или кожа имеют жесткую характеристику, вид которой показан на рис. 1. Чугун и бетон, наоборот, имеют характеристику мягкую, см. рис. 2. Часто в машинах применяются пружины (рессоры) коэффициент жесткости которых зависит от деформации. Применяются также соединительные элементы (муфты) со специальными нелинейными характеристиками. Весьма распространены нелинейности, носящие технологический характер, например, зазоры в зубчатых и шлицевых соединениях.

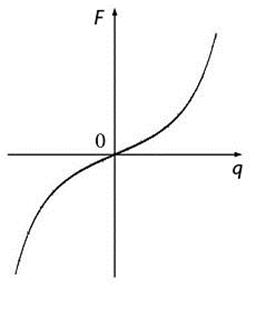
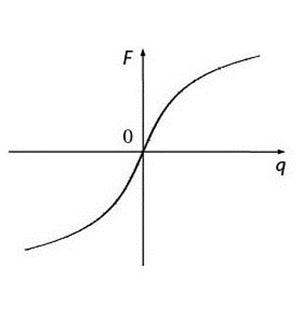
Рис. 1. Жесткая нелинейная Рис. 2. Мягкая нелинейная

характеристика характеристика

Другой вид нелинейности системы имеет место, когда силы сопротивления движению нельзя представить линейной функцией скорости. При этом упругие силы могут иметь и линейный характер.

Значительная часть динамических процессов описывается нелинейными дифференциальными уравнениями с малым параметром вида

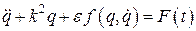, (1)

где 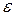– малая величина. Уравнение (1) обязательно строится таким образом, что при 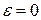оно является линейным. В механике такие модели описывают колебания маятника, подрессоренного экипажа, а также деформируемых систем, в которых связь между перемещениями и деформациями является нелинейной. Например, колебания силовых передач с зубчатым зацеплением, лопаток турбин, лопастей вертолетов, элементов робототехнических систем и т.д. Нелинейными уравнениями описываются также колебания пластин и оболочек, являющихся частями ракетной и космической техники. Кроме того, только нелинейные модели описывают такие явления, как параметрические или автоколебания.

Учение о нелинейных колебаниях зародилось в XVIII столетии и стимулировалось, главным образом, потребностями астрономии, например, знаменитая задача трех тел. Одним из наиболее распространенных методов исследования нелинейных задач, которым с успехом пользовались астрономы, был способ разложения искомых функций, удовлетворяющих дифференциальным уравнениям, по степеням малого параметра 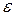, входящего в данные дифференциальные уравнения. Значительно позже появились потребности в решении нелинейных задач в физике, а затем и в механике. Задачи последней потребовали более сложного математического аппарата, и с его развитием появилось новое направление механики, получившее название «нелинейной механики».

Степенные ряды для интегрирования дифференциальных уравнений начали применять одновременно с разработкой основ дифференциального и интегрального исчисления. Уже в ряде статей и мемуаров Ньютона, Лейбница, Якова и Иоганна Бернулли дано систематическое изложение метода неопределенных коэффициентов для решения дифференциальных уравнений. Дальнейший шаг в этом направлении был сделан Эйлером.

В XIX веке появился математический аппарат решения нелинейных дифференциальных уравнений, содержащих малый параметр. Он применялся астрономами для решения задач возмущенного движения планет Солнечной системы. Для примера рассмотрим уравнение

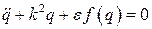, (2)

где 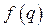– полином. Начальные условия принимаются в виде

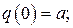
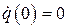, (3)

а начальные условия с ненулевой обобщенной скоростью могут быть выбором начала отсчета времени приведены к виду (3).

Одним из первых метод разложения решения уравнения (2) в ряд по степеням малого параметра 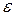предложил Пуассон в своей «Механике». Решение принимается в виде

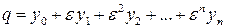. (4)

Здесь 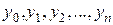– неизвестные функции. Подставляя (4) в уравнение (2), получают систему уравнений:

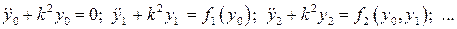(5)

с начальными условиями

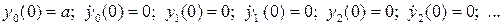
Для четной функции 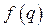решение получается периодическим, но если 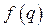будет включать и нечетные степени переменной q, в правой части уравнения системы (5), которым определяются решения 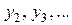наряду с членами, гармонически зависящими от времени, появятся секулярные (вековые) члены вида 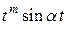и 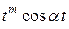, которые при возрастании t будут расти. Таким образом, пользоваться найденным решением можно лишь для малых значений переменной t. Ниже приводится решение уравнения Дуффинга

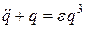(6)

при начальных условиях

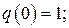
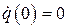, (7)

полученное с точностью до второго приближения

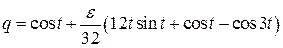. (8)

В связи с вышесказанным появилось много работ, в основном французских математиков, в которых рассматриваются различные способы уничтожения в решении секулярных членов. Среди них наиболее знамениты работы Лапласа и Лагранжа. Однако их методы требуют интегрирования некоторых систем дифференциальных уравнений и приводят к весьма сложным выкладкам.

Можно построить процесс таким образом, чтобы при решении уравнения выбором произвольных или неопределенных величин не уничтожать, а предотвращать появление секулярных членов. Такой способ в 1840 году предлагает М. В. Остроградский, который одним из первых применял асимптотические методы в механике. В качестве примера он рассматривает уравнение (6) при начальных условиях (7) и показывает, что обычный способ дает решение с точностью до величин первого порядка относительно 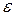выражение (8). При этом великий ученый замечает, что «… однако это выражение станет неточным вследствие множителя t, находящегося вне знака синуса».

В результате он приходит к тому, что нужно изменить частоту колебаний, взяв вместо единицы p, тогда в решении время t содержится уже только под знаком косинуса.

.

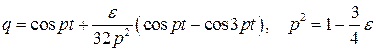Рэлей в своей «Теории звука» рассматривает аналогичное, но более общее уравнение

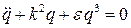(9)

при начальных условиях 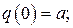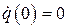. Восстанавливающая сила в (9) симметрична относительно положения равновесия. Позже это уравнение послужило простейшей моделью для описания флаттера упругих систем.