Рассчитаем моменты инерции некоторых тел при различном расположении оси вращения.
1.Кольцо (тонкостенный цилиндр), ось вращения проходит через центр масс. (рис.3).


Рис.3а. Рис.3б.
Пусть кольцо (цилиндр) имеет радиус 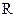 и массу
и массу 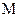 . Для расчета используем формулу
. Для расчета используем формулу 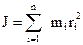 . В этом случае
. В этом случае 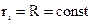 для всех элементарных масс
для всех элементарных масс 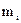 . Поэтому
. Поэтому 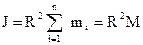 .
.
2. Однородный стержень, ось вращения проходит через конец стержня.
Разобьем стержень на несколько частей длиной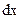 с массой
с массой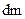 , расположенных на разных расстояниях
, расположенных на разных расстояниях 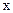 от оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
от оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
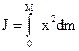
где 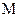 - масса всего стержня. Введем плотность и выразим через нее массу.
- масса всего стержня. Введем плотность и выразим через нее массу.

Рис.4.
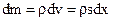 ,
,
где 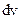 - объем элемента стержня площадью поперечного сечения
- объем элемента стержня площадью поперечного сечения 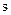 и длины
и длины 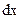 . Тогда
. Тогда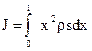 ,
,
где 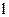 - длина стержня. После интегрирования получаем:
- длина стержня. После интегрирования получаем:
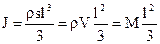 ,
,
где 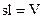 - объем всего стержня. Таким образом
- объем всего стержня. Таким образом
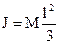 .
.
Если ось вращения стержня проходит через центр масс стержня, то
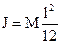 .
.
В таблице 1 приведены значения моментов инерции некоторых тел.
Таблица 1
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиусом R | Ось симметрии | (1/2)mR2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12)ml2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3)ml2 |
| Шар радиусом R | Ось проходит через центр шара | (2/5)mR2 |
Если известен момент инерции 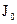 относительно оси проходящей через центр масс, то можно найти момент инерции относительно некоторых других осей по теореме Штейнера:
относительно оси проходящей через центр масс, то можно найти момент инерции относительно некоторых других осей по теореме Штейнера:
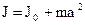 (15)
(15)
Момент инерции твердого тела относительно любой оси равен моменту инерции относительно оси параллельной данной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями.

Рис.5.
Применим теорему Штейнера для определения момента инерции однородного стержня, длиной 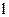 . Пусть
. Пусть 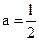 . Величина
. Величина 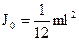 (смотри таблицу). Тогда
(смотри таблицу). Тогда

Рис.6.
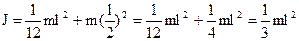 .
.
 2014-02-09
2014-02-09 3129
3129
