Неинерциальные системы отсчета. Силы инерции

Законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, которые движутся ускоренно относительно инерциальных систем, называют неинерциальными. Внеинерциальной системе отсчета ускорение тела отличается от ускорения 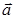в инерциальной системе на величину :

– = .

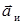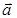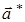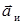Пусть результирующая всех сил, обусловленных действием на данное тело со стороны других тел, равна 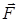, тогда согласно второму закону Ньютона ускорение тела относительно любой инерциальной системы отсчета равно

.

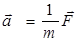Ускорение же тела относительно неинерциальной системы можно представить в виде

= – = .

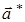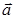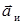Отсюда следует, что при 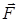= 0 тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением 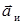, т. е. так, как если бы на него действовала сила, равная – m.

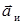Сказанное означает, что при описании движения в неинерциальных системах можно пользоваться уравнениями движения Ньютона, если наряду с силами воздействия тел друг на друга, учитывать так называемые силы инерции 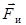. Силы инерции следует полагать равными произведению массы тела на взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной систем отсчета:

.

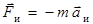Следовательно, уравнение движения в неинерциальной системе отсчета будет иметь вид:

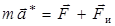. (2.3)

Поясним наше утверждение примерами.

Рис. 2.1

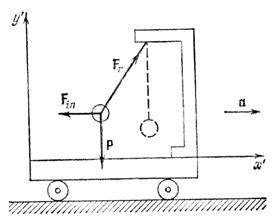
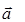1. Рассмотрим тележку с укрепленным на ней кронштейном, к которому подвешен на нити шарик (рис. 2.1). Пока тележка покоится или движется без ускорения, нить расположена вертикально. Приведем тележку в поступательное движение с ускорением . Нить отклонится от вертикали на такой угол, чтобы результирующая сил 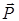и 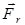сообщала шарику ускорение 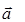. Относительно системы отсчета, связанной с тележкой, шарик покоится, несмотря на то, что результирующая сил 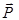и 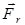отлична от нуля. Отсутствие ускорения шарика по отношению к этой

системе отсчета можно формально объяснить тем, что, кроме сил 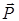и 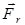на шарик действует и сила инерции .

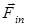Следовательно, в неинерциальной системе отсчета при ускоренном прямолинейном движении этой системы на тела неподвижные относительно этой системы действует сила инерции

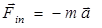. (2.4)

Рис. 2.2

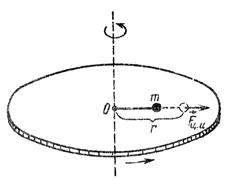
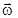2. Пусть, например, на горизонтальной платформе, которая может вращаться вокруг вертикальной оси, лежит тело массой m, связанное с центром вращения О упругим элементом (рис. 2.2). Если платформа начнет вращаться с постоянной угловой скоростью (и, следовательно, превратится в неинерциальную систему отсчета), то благодаря трению тело тоже будет вовлечено во вращение. Вместе с тем оно будет перемещаться в радиальном направлении от центра платформы до тех пор, пока возвращающая сила упругости не остановит это перемещение. Тогда тело начнет вращаться на расстоянии r от центра О. С точки зрения наблюдателя, связанного с платформой, перемещение

шара относительно нее обусловлено некоторой силой 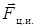. Это сила инерции, поскольку она не вызвана действием на шар других определенных сил; ее называют центробежной силой инерции. Очевидно, что центробежная сила инерции равна по модулю и противоположна по направлению центростремительной силе, действующей на тело.

Поэтому

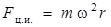. (2.5)