В ПП кроме процессов генерации (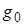 или в общем случае g) и рекомбинации (
или в общем случае g) и рекомбинации (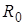 ) существует еще движение носителей в зонах. Рассмотрим на примере электронного ПП (рис. 2.10). Движение носителей в зоне происходит в результате неравномерного распределения по оси х (диффузия) или под действием внешнего поля Е (дрейф). Эти процессы характеризуются потоками или плотностями токов. Если в ПП выделить единичный объем
) существует еще движение носителей в зонах. Рассмотрим на примере электронного ПП (рис. 2.10). Движение носителей в зоне происходит в результате неравномерного распределения по оси х (диффузия) или под действием внешнего поля Е (дрейф). Эти процессы характеризуются потоками или плотностями токов. Если в ПП выделить единичный объем 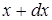 , то в него будут входить и выходить электроны. Из математического анализа известно, что за единицу времени в единичном объеме этот процесс характеризуется частной производной
, то в него будут входить и выходить электроны. Из математического анализа известно, что за единицу времени в единичном объеме этот процесс характеризуется частной производной 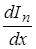 , а с учетом трех координат
, а с учетом трех координат 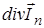 .
.
Аналогично для дырок в валентной зоне в результате движения мы получим изменение концентрации дырок 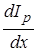 или
или 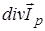 .
.
В результате всех процессов в ПП изменение концентраций со временем может быть описано уравнениями
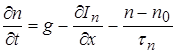 ;
; 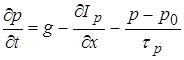
Эти выражения носят название уравнений непрерывности.
Учитывая, что 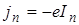 и
и 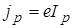
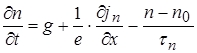 ,
,
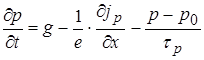 .
.
Уточним 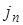 и
и 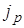 .
.
Рассмотрим диффузионную составляющую потоков. Из общей физики известно, что
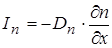 ,
, 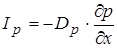 .
.
Знак минус говорит о движении в сторону меньших концентраций. Если учесть зависимость 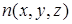 или в общем случае
или в общем случае 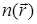 , то вместо
, то вместо 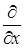 мы должны поставить
мы должны поставить 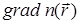 .
. Здесь
Здесь 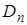 и
и 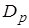 – коэффициенты диффузии электронов и дырок соответственно. Они связаны с подвижностью соотношениями Эйнштейна:
– коэффициенты диффузии электронов и дырок соответственно. Они связаны с подвижностью соотношениями Эйнштейна:
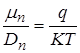 и
и 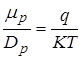 .
.
В принципе, в процессе диффузии атомов 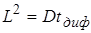 , где L – глубина диффузии, t – время диффузии.
, где L – глубина диффузии, t – время диффузии.
У нас частицы имеют ограниченное время жизни. Поэтому они диффундируют, пока существуют. L принимает смысл пути, проходимого носителем за время жизни. В ПП L называется диффузионной длиной. Для электронов 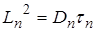 , для дырок
, для дырок 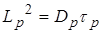 .
.
Переходя от потоков к плотностям токов, получим:
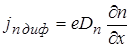 ,
, 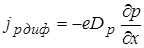
Диффузия носителей приводит к пространственному разделению зарядов и к возникновению электрического поля (возможно и внешнее воздействие). Это поле приводит к движению зарядов, т.е. к появлению тока дрейфа.
Подставив 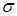 , получим:
, получим:
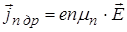 ,
, 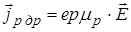 .
.
Ток для электронов и дырок будет складываться из 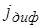 и
и 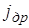 .
.
Для электронов 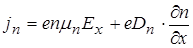 .
.
Для дырок 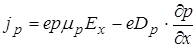 .
.
Полный ток в ПП 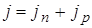 .
.
Следует отметить, что в условиях равновесия, т.е. при отсутствии внешнего воздействия, 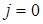 .
.
Уточним уравнение непрерывности с учетом полученных выражений.
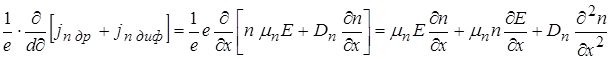 .
.
Для дырок разница будет лишь в знаке при 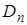 :
:
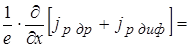
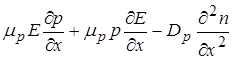 .
.
Окончательно имеем:
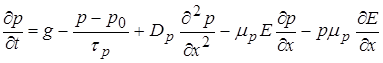 ,
,
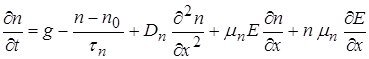 .
.
Это полные уравнения непрерывности. Они являются основными уравнениями при рассмотрении работы диодов и биполярных транзисторов.
Если нет генерации и отсутствует дрейф, то получим уравнение диффузии
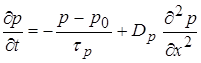 или
или 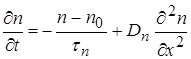 .
.

 2014-02-24
2014-02-24 796
796








