Предполагаемого закона распределения. Статистическая оценка параметров

Статистическая оценка параметров

Принимать по 1 капсуле в день с небольшим количеством воды. 60 капсул достаточно для лечения 60 дней при употреблении рекомендуемого суточного количества 1 капсуле.

Новый продукт компании, который сочетает в себе наиболее активные ингредиенты для защиты глаз. Защищает сетчатку от пагубного излучения компьютера и телевизора, препятствует развитию дистрофических процессов в сетчатке, снижает риск развития катаракты

Показания к применению:

· для профилактики возрастных изменений в сетчатке (макулодистрофии) и катаракты у лиц старше 50-ти лет;

· - при систематической работе с компьютером в любом возрасте;

· - при близорукости для профилактики осложнений;

· - при синдроме «усталых глаз»;

· - при работе, связанной с воздействием яркого света (сварка, софиты);

· - при снижении темновой адаптации (куриная слепота);

· - при занятиях спортом – горными лыжами, виндсерфингом, альпинизмом (из-за высокой отражательной способности больших водных и снежных поверхностей).

Применение:

Пусть требуется изучить количественный признак генеральной совокупности. Изначально закон распределения генеральной совокупности неизвестен, но в результате графической обработки статистических данных можно выдвинуть гипотезу о законе распределения.

Согласно вероятностному смыслу гистограммы линия, проведенная через середины верхних оснований прямоугольников или полигон относительных частот, напоминает по форме график плотности вероятности 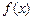. Приближенно это график 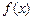для непрерывной величины, представленной генеральной совокупностью.

Следует сравнить полигон относительных частот изучаемой случайной величины с известными из теории вероятностей графиками 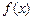основных распределений (рис. 1–3). Выбрать похожую по форме 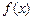и выдвинуть гипотезу о законе распределения исследуемой непрерывной случайной величины.

Допустим, выдвинута гипотеза о том, какое именно распределение имеет признак. Естественно, возникает задача оценки параметров, которыми определяется это распределение.

Например, если наперед известно, что признак имеет равномерное распределение, то необходимо оценить параметры a и b, которыми это распределение определяется и которые выражаются через математическое ожидание М (Х) и среднее квадратическое отклонениеσ _х:

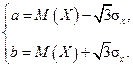
Если же есть основания считать, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) два параметра m и σ, которые совпадают с математическим ожиданием М (Х) и средним квадратическим отклонением σ _х, соответственно:

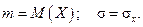
Если же есть основания считать, что признак имеет показательное распределение, то необходимо оценить параметр λ, которым это распределение определяется и которое выражается через математическое ожидание:

.

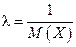Обычно в распоряжении исследователя имеются лишь данные выборки, например, значения количественного признака х ₁, х ₂..., х_{n ,} полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.

Можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

В результате обработки статистических данных оцениваются различные выборочные характеристики случайной величины Х: выборочное среднее 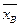, выборочная дисперсия 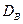, выборочное среднее квадратическое отклонение 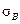. Эти характеристики используются в качестве приближенных значений неизвестных числовых характеристик изучаемой случайной величины Х (неизвестных генеральных характеристик). Так, выборочное среднее 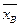используется как приближенное значение математического ожидания М (Х)(генеральной средней), а выборочная дисперсия 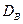– как приближенное значение генеральной дисперсии D (X).

Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется ее точечной статистической оценкой.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Рассмотрим эти требования.

Пусть θ* есть статистическая оценка неизвестного параметра θ теоретического распределения.

Несмещенной называют статистическую оценку θ*, математическое ожидание которой равно оцениваемому параметру θ при любом объеме выборки:

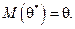
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п)имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема (п велико) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при 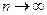стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при 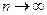стремится к нулю, то такая оценка оказывается и состоятельной.

Оказывается, что выборочная средняя 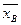является несмещенной и состоятельной оценкой генеральной средней М (Х).

Если в качестве оценки генеральной дисперсии D (X)принять выборочную дисперсию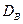, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия 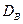, как можно доказать, является смещенной оценкой D (X), другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

.

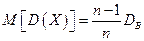Легко «исправить» выборочную дисперсию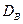так, чтобы ее математическое ожидание было равно генеральной дисперсии D (X). Достаточно для этого умножить 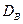на дробь .

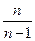Сделав это, получим «исправленную дисперсию», которую обычно обозначают через s ²:

,

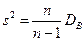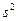при этом является также состоятельной оценкой генеральной дисперсии D (X).

Для оценки же среднего квадратнческого отклонения генеральной совокупности используют «исправленное» среднее квадратическос отклонение, которое равно квадратному корню из исправленной дисперсии:.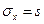

Для записи гипотетических функций распределения необходимо заменить в соответствующих аналитических формулах предполагаемого распределения параметры распределения их точечными оценками.

С помощью формул, соответствующих гипотетическому закону распределения, можно вычислить теоретические вероятности попадания случайного признака в каждый интервал.

Построив на одном графике полигон относительных частот статистического распределения и гипотетическую теоретическую плотность распределения, можно сравнить эти кривые.