Вероятность, приходящаяся на единицу длины этого интервала, определится как

Плотность распределения вероятностей случайной величины и гистограмма

ТЗР-4. Плотность распределения случайной величины (дифференциальная функция распределения СВ)

Плотность распределения вероятностей СВ (другое название – дифференциальная функция распределения СВ) является очень распространенным способом задания закона распределения непрерывных СВ.

Если закон распределения непрерывной случайной величины Х задан при помощи интегральной функции F(x), то вероятность того, что СВ примет значение в интервале от х до х + Δх равна разности значений интегральной функции распределения на границах интервала:

Р(х < Х < х + Δх) = F(х + Δх) - F(х).

(F(х + Δх) - F(х))/ Δх

Если теперь устремить Δх к нулю и перейти к пределу, то получим первую производную интегральной функции распределения, которую называют плотностью распределения вероятности СВ и обозначают f(x):

lim(F(х + Δх) - F(х))/ Δх = F'(x) = f(x) (23)

Δх→0

Рассмотрим основные свойства плотности распределения вероятностей:

Свойство 1. Плотность распределения вероятностей существует только для непрерывных СВ. Для дискретных СВ производная не существует, и поэтому этот способ задания закона распределения для них неприменим.

Свойство 2. Плотность распределения вероятностей всегда неотрицательна:

f(x) ≥ 0, так как является производной неубывающей функции.

Свойство 3. При значениях СВ, стремящихся к ±∞, плотность распределения равна нулю или стремится к нулю.

Свойство 4. График дифференциальной функции распределения называется кривой распределения (рис. 40) и весьма нагляден (кривые для разных законов легко отличить друг от друга).

Свойство 5. Так как f(x) = F'(x), то F(x) =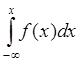. (24)

Геометрически (рис. 41) интегральная функция распределения – это площадь под кривой распределения, лежащая левее точки а.

Свойство 6. Вероятность того, что случайная величина Х примет значение в интервале (а; b), есть интеграл от плотности распределения в пределах от а до b:

Р(а < Х < b) = F(b) – F(a) =

== .

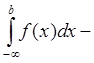
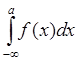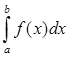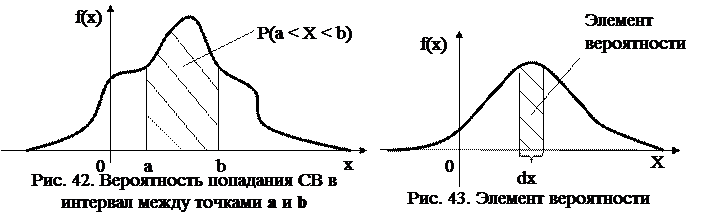Геометрически (рис. 42) вероятность попадания СВ в интервал между точками а и b – это площадь под кривой распределения, лежащая между точками а и b.

Свойство 7. Произведение f(x)dx называется элементом вероятности (рис. 43).

Свойство 8. Вся площадь, лежащая под кривой распределения, равна единице.

Это свойство несложно пояснить:

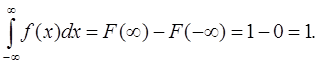
Таким образом, если в одних и тех же осях построено несколько кривых распределения, площади под ними должны быть одинаковыми. и равными единице.

Свойство 9. Размерность плотности распределения вероятностей обратна размерности случайной величины.

Это свойство можно пояснить следующим образом:

Площадь под кривой распределения (рис. 44) по своему вероятностному смыслу является вероятностью. Как и всякая вероятность, эта площадь безразмерна. С другой стороны площадь есть произведение длин отрезков по осям абсцисс и ординат, т.е. по размерностям – произведение размерности СВ на размерность плотности распределения. Так, если случайной величиной является ток, измеряемый в амперах, то плотность распределения должна измеряться в 1/А – тогда произведение размерностей А ∙ 1/А даст безразмерную величину.

СтЗР-4. Гистограмма относительных частот

Статистической аналогией кривой распределения является гистограмма относительных частот. Она строится на основании группированного статистического (вариационного) ряда (табл.6).

Порядок построения гистограммы (рис.45):

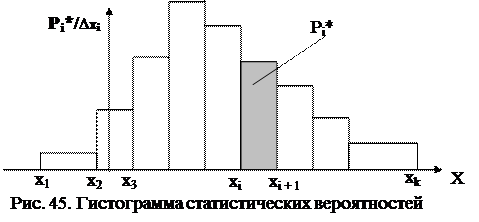1. На оси случайной величины откладываются отрезки ∆x_i, равные ширине интервалов (разрядов). Чаще всего они имеют одинаковую длину, но иногда (обычно по краям распределения) длина интервалов может быть увеличена в 2…3 раза по сравнению с центральными разрядами.

2. На отрезках ∆x_i, как на основаниях строятся прямоугольники, площади которых численно равны статистическим вероятностям р _i * попадания случайной величины в соответствующий разряд. Для того чтобы выполнить это условие необходимо правильно определить высоту каждого из прямоугольников.

Площадь каждого прямоугольника гистограммы – это статистическая вероятность P_i*=n_i/N. С другой стороны площадь прямоугольника: S_i = h_iΔx_i, где h _i – высота i -го прямоугольника гистограммы. Отсюда h _i = =.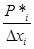

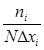Так как знаменатель в этом выражении для каждого разряда одинаков (при условии одинаковой их ширины), то высота h_i пропорциональна n_i. Откладывая высоты прямоугольников гистограммы в выбранном масштабе пропорционально частотам n_i. разрядов, можно существенно упростить последующий анализ статистических данных.

Основные параметры законов распределения случайных величин

Закон распределения вероятностей позволяет максимально подробным образом охарактеризовать случайную величину. Однако определить его при решении практических задач непросто. Это требует углубленного исследования, сбора большого объёма информации. Но для большого круга задач нет необходимости находить сам закон. Достаточно воспользоваться отдельными параметрами этого закона.

Параметр закона распределения – это числовая характеристика того или иного свойства случайной величины.

Первая группа параметров – это, так называемые, параметры положения случайной величины. К ним относятся параметры, которые характеризуют расположение случайной величины на числовой оси. К ним относятся мода, медиана и математическое ожидание.