2014-02-24
2041
Для непрерывных случайных величин вероятность того, что они примут какое-то конкретное значение, равна нулю:
Р(Х = х) = 0.
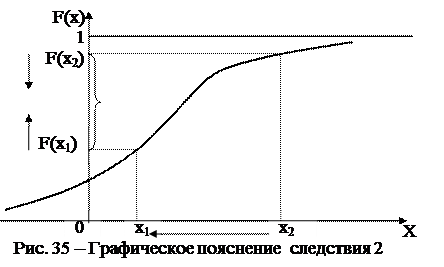Действительно (рис.35), если приближать значение х2 к значению х1 (уменьшать размер интервала) пока они не сравняются (х1 = х2.),то интервал превратится в точку (СВ примет конкретное значение) Тогда значения функции F(х). также будут сближаться, пока не сравняются и разность между ними станет нулевой.
На первый взгляд это следствие кажется парадоксальным. Как же так? Ведь СВ всегда в опыте примет какое-то конкретное значение. Например, напряжение в сети может равняться 381 В. Однако наряду с этим значением напряжение может принять значения 381,1 В, 381,11 В 380,111 В и т. д, то есть как для любой непрерывной СВ количество возможных значений для него бесконечно велико. Между этим бесконечным числом возможных значений делится их общая вероятность равная единице. Парадоксальность этого следствия сродни следующим парадоксам: линия конечной длины состоит из точек с нулевыми размерами; тело конечной массы состоит из точек нулевой массы и т.д.
|
|
|
Свойство 5.
Если случайная величина Х принимает значения только в интервале (а; b), то интегральная функция распределения F(x) равна нулю при значениях х ≤ а и равна единице при значениях х > b.
Действительно, если Х примет значения меньше а, то её значений расположенных левее согласно условию нет. Поэтому Р(Х < а) = F(а) = 0, как вероятность невозможного события.
С другой стороны, если для такой СВ взять какую-то точку расположенную вправо от в, то событие Х < в является достоверным (все значения СВ расположены левее в по условию) и его вероятность равна единице.
Из этого свойства существует следствие.
Следствие. Если непрерывная случайная величина Х принимает значения в интервале от -∞ до +∞ (занимает всю числовую ось), то предел интегральной функции распределения при значениях Х, стремящихся к -∞, равен нулю, а при значениях Х, стремящихся к +∞, равен единице:
lim F(x) = 0, lim F(x) = 1.
х→-∞ х→+∞
Выполнение этого свойства можно наблюдать на графиках интегральной функции распределения вероятностей (рис.29, 30, 32 …35).
Интегральная функция распределения вероятностей широко применяется для задания законов распределения различных СВ, но имеет один недостаток. Этим недостатком является невысокая наглядность. Если изобразить графики (1, 2, 3) интегральной функции нескольких непрерывных СВ в одних осях (рис. 36), то их нетрудно отличить друг от друга.
Однако все три графика очень похожи: функции возрастают, их значения лежат в одинаковом интервале (0;1). Если расположить эти графики на разных рисунках отличить их друг от друга будет непросто.
|
|
|
Гораздо большей наглядностью обладает другой способ задания закона распределения - плотность распределения случайной величины.
СтЗР-3. Статистическая функция распределения
Статистическая (эмпирическая) функция распределения F*(x) является аналогом теоретической функции распределения вероятностей:
F*(x) = P*(X<x), (22)
где P* (X<x) - статистическая вероятность того, что случайная величина Х приняла в опыте значения меньше, чем произвольно взятое значение х.
Эту функцию, полученную опытным (эмпирическим) путём, часто называют функцией накопленных (кумулятивных) частостей рх*.
Статистическую функцию распределения вычисляют на основе статистического ряда распределения, суммируя частоты (числа наблюдений) для вариант, расположенных левее значения х:
P*(X<x) = nx/N,
где nx – число наблюдений (частота), в которых случайная величина Х приняла значение меньше х;
N – число проведенных опытов (объём статистики).
Если случайная величина дискретна и количество наблюдавшихся значений (вариант) невелико, то статистическая функция распределения вычисляется на основе негруппированного статистического ряда и внешне не отличается от функции распределения дискретной СВ (рис. 37). Её принципиальным отличием от теоретической функции является учёт не теоретических вероятностей, а относительных частот наблюдения отдельных значений СВ (этим частотам равны высоты «ступенек» графика). Например, статистическая функция распределения оценок студентов на экзамене строится на основе ограниченного (не бесконечного) количества экзаменационных ведомостей.
Если статистическая функция распределения строится на основе группированного статистического ряда (он используется в тех случаях, когда количество вариант велико), то она представляет из себя ломаную линию (рис. 38).
Каждый участок (a;b) ломаной (рис. 39) соответствует интервалу (разряду) статистического ряда и представляет собой отрезок прямой, что характерно для равномерного закона распределения случайной величины внутри интервала (х1;х2).
