Геометрическая интерпретация

Рассмотрим n-мерное векторное пространство Rⁿ, снабженное стандартным евклидовым скалярным произведением: 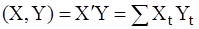, где X¢ – транспонированная матрица, т.е. в данном случае 1xn – вектор-строка. Пусть

,

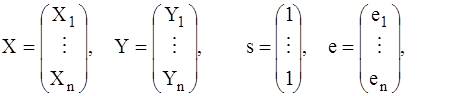
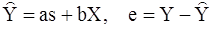где a, b – числовые коэффициенты, 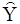– вектор, лежащий в двумерной гиперплоскости p, натянутой на векторы s, X. (Здесь мы снова предполагаем, что векторы s и X – неколлинеарные). Поставим задачу: найти такие a, b, чтобы вектор e имел наименьшую длину. Другими словами, мы хотим наилучшим образом аппроксимировать вектор Y вектором 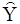, лежащим в подпространстве p. Очевидно, решением является такой вектор 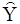, для которого вектор e перпендикулярен плоскости p. Для этого необходимо и достаточно, чтобы вектор e был ортогонален векторам s и X, порождающим плоскость p:

,

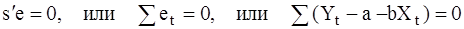(13)

.

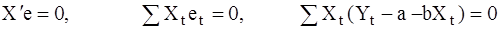Нетрудно заметить, что мы снова получили необходимые условия экстремума (8).