2014-02-24
556
Статистические свойства МНК-оценок параметров регрессии. Доверительные интервалы
Пусть выполняется условие нормальной линейной регрессионной модели e ~ N (0, s2 In),т.е. e – многомерная нормально распределенная случайная величина, или, что то же самое, Yt имеют совместное нормальное распределение, так как они являются линейными функциями от Yt (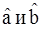
есть функции от Yt) (см. формулы (10) и (11)):
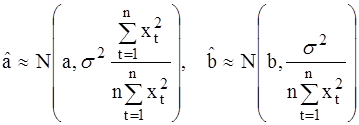. (26)
Если гипотеза нормальности ошибок не выполняется, то выражение (26), вообще говоря, неверно, однако при некоторых условиях регулярности относительное поведение Xt при росте n, оценки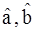 
имеют асимптотически нормальное распределение, т.е. (26) выполняется асимптотически при n ® µ.
14. Распределение оценки дисперсии ошибок S2
Покажем, что в случае нормальной линейной регрессионной модели, т.е. когда e – многомерная нормально распределенная случайная величина, выполняется условие
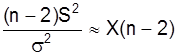
Используя формулу для определения дисперсии оценки b, имеем
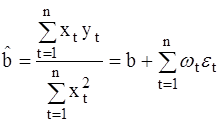. (27)
Подставив (27) в уравнение регрессии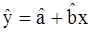 
, получим следующую формулу для остатков регрессии:
 =
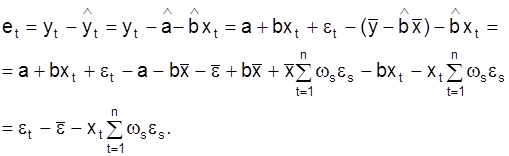| (28) |
Представим выражение (28) в векторной форме:
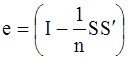. (29)
Здесь S – nх1 – вектор-столбец, состоящий из одних единиц,
e = (e1,e2,……, en)׳, e = (e1, e2, ……., en)׳,
А – nxn – матрица.
Проверим, что матрица A=I-1/n·SS׳-xw׳ (29) является идемпотентной: A׳= A, так как (SS`)`=S``S`=SS` и
;
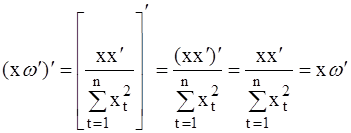A2=(I–1/nSS`-xw`)2=I+1/n2SS`SS`+xw`xw`-2/nSS`-2xw`+
+1/nSS`xw`+1/nxw`SS`=I–1/nSS`+xw`-2xw`=I–1/nSS`-xw`=A,
так как SS` = n, S`x = w`S = 0.
По условиям классической регрессионной модели e/s ~ N (0, In). Таким образом,
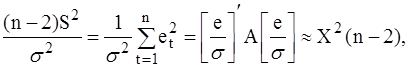(30)
что и требовалось доказать.
15. Независимость S2 и МНК-оценок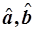 
Так как оценка дисперсии ошибок S2 является функцией от остатков регрессии et, то для того чтобы доказать независимость S2 и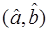 
, достаточно доказать независимость et и 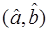. Оценки 
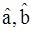так же, как и остатки регрессии et, являются линейными функциями ошибок et (см. формулы (10), (11) и (29)) и поэтому имеют нормальное совместное распределение. Известно, что два случайных вектора, имеющих совместное нормальное распределение, независимы тогда и только тогда, когда они некоррелированы. Таким образом, чтобы доказать независимость S2 и 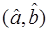, нам достаточно доказать некоррелированность et и .
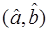Обозначим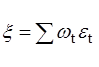 
, тогда из (28) 
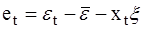, а из уравнения (27) следует, что b = b+x.
Тогда
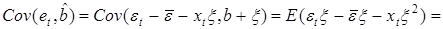
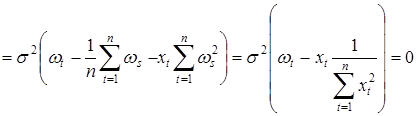. (31)
Таким образом, et и b независимы при всех t, что и требовалось доказать.
16. Проверка гипотезы b=b0
Из выражения (26) имеем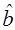 
= b ~ N(0, sb2), где 
.
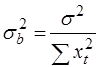Оценка дисперсии оценки 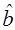может быть получена по формуле 
.
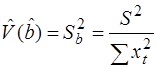Таким образом,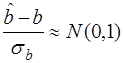 
, а из (30) 
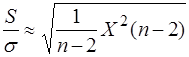, т.е. по определению статистики Стьюдента
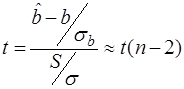
или, замечая, что
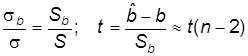, (32)
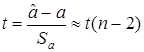. (33)
Итак, мы показали, что в случае нормально распределенных ошибок величина (32) распределена по закону Стьюдента. Заметим, что при определенных условиях регулярности на xt соотношения (32) и (33) справедливы асимптотически и без предположения о нормальности ошибок регрессии.
Статистику уравнения (32) можно использовать для проверки гипотезы Ho: b = b0. Вопреки альтернативной гипотезе H1: b ¹ b0. Предположим, что верна гипотеза Ho , и зададимся, например, 5%-ной квантилью t-распределения с (n–2) степенями свободы tc (при 40 степенях свободы tc=2,021), т.е.
.
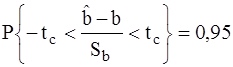Мы отвергаем гипотезу Ho (и принимаем H1) с 95%-ным доверительным уровнем, если êt÷>tc («редкое» событие с точки зрения гипотезы Ho), в противном случае мы не можем отвергнуть Ho (и принимаем Ho).
Разрешив неравенство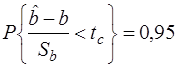 
относительно b, получим
,
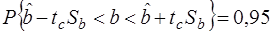т.е.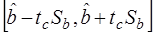 
– 95%-ный доверительный интервал для b.
Доверительный интервал накрывает истинное значение параметра b с заданной вероятностью (в данном случае – 95%).
Наиболее просто выглядит t-статистика при гипотезе Ho: b = 0, а именно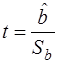 
. Это значение и приводится всеми компьютерными пакетами в результате регрессии. Значение çtô > tc (tc» 2) для 95%-ого уровня значимости позволяет сделать вывод об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) X и Y. Малые значения t-статистики соответствуют отсутствию достоверной статистической связи объясняющих переменных X и Y.
