Модель канала с независимыми ошибками

Основные аналитические модели дискретных каналов

Для аналитического решения задач по определению эффективности систем связи требуется применение математических моделей ДК. Такие модели должны описывать некоторые закономерности потоков ошибок. Модель канала должна рассматриваться как математическая основа позволяющая создать применяемые на практике методы расчета параметров системы связи.

Поэтому естественно предъявить к математическим моделям ряд требований:

1. Соответствие закономерностей распределения ошибок, получаемых при использовании модели, действительным закономерностям, наблюдаемым в реальных каналах.

2. Возможность создания на основе данной модели методов расчета параметров систем связи, точность которых удовлетворяла бы требованиям инженерной практики.

3. Минимальное количество параметров, используемых при описании потоков ошибок в модели. Простота экспериментальных измерений этих параметров на реальных каналах связи.

В настоящее время разработано большое количество моделей, описывающих ДКС. Рассмотрим наиболее характерные из этих моделей.

Данная модель разработана для симметричного ДКС без памяти, т.е. для потока независимых ошибок. В этом случае для описания ДКС достаточно знать единственный параметр − р₀ − вероятность появления ошибки на е.э.

Пусть как и ранее вероятность ошибочного приема е.э. равна р₀, тогда вероятность правильного приема этого е.э. равна 1− р₀.

Правильный прием всей КК из “n” е.э. возможен, если все “n” элементов приняты без ошибок. Согласно теореме о совместимых и независимых событиях эта вероятность равна произведению вероятностей каждого события, т.е. − (1−р₀)ⁿ.

Тогда вероятность приема КК длиной “n”:

P(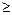1,n) = 1−(1−p₀)ⁿ (2.32)

Применим формулу бинома Ньютона:

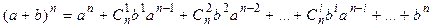
где 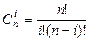− число сочетаний;

обозначим:

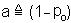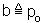; ; тогда (а + b)ⁿ = 1 (в наших обозначениях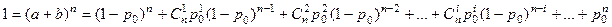) и или .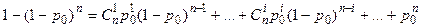

левая часть есть Р(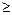1;n), поэтому получим:

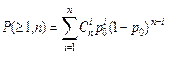(2.33)

− это вероятность ошибочного приема КК длинной “n”,хотя бы с одной ошибкой.

Слагаемые (2.33) означают вероятность появления ошибок кратности точно “ℓ” в КК длинной “n”, т.е.:

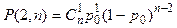(2.34)

..................

Вероятность появления ошибок кратности ℓ и выше определяется выражением:

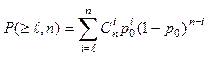(2.35)

Получим приближенную формулу для модели:

P(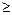1,n) = 1−(1−p₀)ⁿ (2.36)

Для разложения (1−p₀)ⁿ используем бином Ньютона:

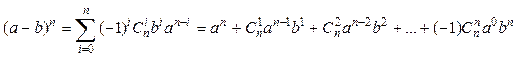(2.37)

Учтем, что а = 1 и b = р₀. Поскольку р₀<< 1, поэтому слагаемыми 2 порядка и выше можно пренебречь. Получим:

(1−p₀)ⁿ = 1 − n p₀ (2.38)

Окончательно получаем:

Р ( (2.39)

Широко используется и кроме того является основой для построения других более сложных моделей, лучше отражающих статистические характеристики реальных ДК.