2014-02-24
609
Двухпараметрическая модель(модель ВКАС, модель Пуртова)
Экспериментальные исследования показали, что зависимость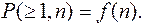 
при n от 1до 500 хорошо аппроксимируется прямыми линиями при логарифмическом масштабе по обеим осям координат.
Рассмотрим подобную зависимость для коммутируемого канала ТЧ кабельной линии при вероятности ошибки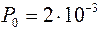 
- (рис 2.15) –прямая 3.
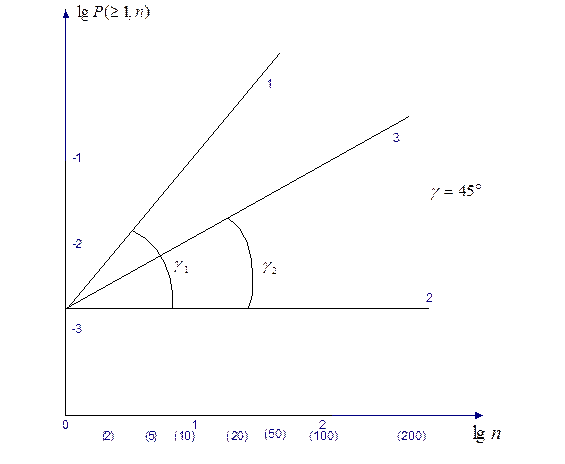
Рис.2.15 Зависимость 
На рис.2.3 показаны два предельных варианта. Первый вариант - равномерное распределение независимых ошибок (прямая 1), а второй вариант - группирование ошибок в одну пачку (прямая 2).
Прямая 1 отражает зависимость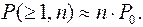 
(См.формулу (2.39).
Действительно: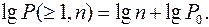 
(2.42)
Это есть уравнение прямой пересекающей ось ординат под углом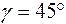 
в точке 
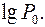Еще раз напоминаем, что данная прямая описывает симметричный ДК с равномерно распределенными независимыми ошибками.
Прямая 2 - описывает канал, в котором ошибки появляются плотной группой. В этом случае (см. табл. и рис.2.15) вероятность появления искажения КК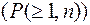 
не зависит от длины КК-“n”.
Поэтому: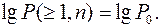 
(2.43)
Это есть уравнение прямой, параллельной оси абсцисс и пересекающейся с осью ординат в точке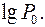 
Прямая 3- экспериментальная зависимость. Она находится между указанными границами и имеет угловой наклон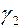 
. Уравнение этой прямой имеет вид
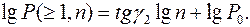
Обозначим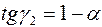 
и проведем операцию, обратную логарифмированию, получим:
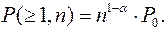(2.44)
Величина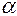 
называется показателем группирования ошибок.
Если 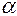=0- то ошибки независимы и равномерно распределены, т.е. приходим к формуле (1.10) (прямая 1).
Если 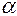=1, то это другой предельный случай –все ошибки сгруппированы в одну пачку (прямая 2).
В реальных каналах 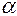лежит в пределах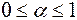 
Например, для коммутируемых ТЧ (телефонных) каналов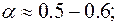 
для радиорелейных каналов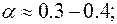 
Для определения вероятности появления L и более ошибок в КК длиной «n» можно воспользоваться формулой:
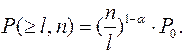(2.45)
Вероятность появления точно L ошибок определяется выражением:
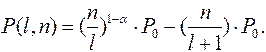(2.46)
Модель Пуртова достаточно хорошо отражает основные свойства ДКС. Однако коэффициент 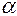может быть определен только экспериментально.
