Классификация помехоустойчивых кодов
Рис. 4.6
Малые точки означают запрещённые КК. Переход от одной точки к другой соответствует искажению одного разряда.
Обозначим 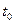 - кратность гарантированно обнаруживаемых ошибок, а
- кратность гарантированно обнаруживаемых ошибок, а
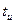 - кратность гарантированно исправляемых ошибок.
- кратность гарантированно исправляемых ошибок.
Ошибка не обнаруживается, если одна разрешённая КК переходит в другую разрешённую КК. Следовательно, для обнаружения всех ошибок кратности до 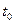 включительно необходимо, чтобы кодовое расстояние
включительно необходимо, чтобы кодовое расстояние 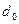 определялось неравенством:
определялось неравенством:
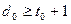 или
или 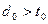 ,
, 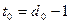 (4.18)
(4.18)
Это видно из рис. 4.6.
Для обеспечения возможности исправления всех ошибок кратности до 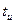 включительно необходимо, как мы уже рассматривали. Чтобы принятая КК осталась в подмножестве запрещённых КК, которое ей принадлежит – на рис. 2.6. Эти подмножества отделены пунктирными линиями. Для этого случая:
включительно необходимо, как мы уже рассматривали. Чтобы принятая КК осталась в подмножестве запрещённых КК, которое ей принадлежит – на рис. 2.6. Эти подмножества отделены пунктирными линиями. Для этого случая:
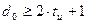 или
или 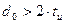 (4.19)
(4.19)
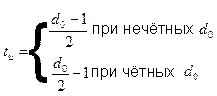
Чтобы код обнаруживал и исправлял ошибки, требуется:
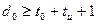 (4.20)
(4.20)
Рассмотренные формулы (4.18), (4.19), (4.20) указывают на минимальное количество обнаруживаемых и исправляемых ошибок. На практике будут обнаруживаться и исправляться ошибки и большей кратности, поскольку расстояние между отдельными КК может быть больше, чем 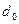 . Однако процент таких ошибок невелик.
. Однако процент таких ошибок невелик.
Другой важной характеристикой кодов выступает вес КК. Под весом КК двоичного кода понимается количество 1 в данной КК - 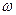 .
.
Для наименьшего веса КК справедливы соотношения:
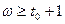
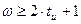 (4.21)
(4.21)
Необходимое кодовое расстояние 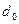 , а значит, и корректирующие свойства кода, определяются его относительной избыточностью, под которой понимается:
, а значит, и корректирующие свойства кода, определяются его относительной избыточностью, под которой понимается:
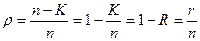 (4.22)
(4.22)
где n – общее число разрядов;
K – число информационных разрядов;
R – скорость кода;
R – число проверочных разрядов в КК.
Задача построения избыточного кода сводится к выбору из 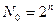 КК таких
КК таких 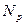 n-разрядных КК, для которых обеспечивается максимально возможное расстояние d. Для этого прежде всего необходимо определить требуемое число проверочных разрядов r. В общем виде эта задача до настоящего времени не решена. Точная формула, связывающая
n-разрядных КК, для которых обеспечивается максимально возможное расстояние d. Для этого прежде всего необходимо определить требуемое число проверочных разрядов r. В общем виде эта задача до настоящего времени не решена. Точная формула, связывающая 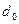 и r, известна только для
и r, известна только для 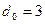
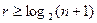 (4.23)
(4.23)
Для остальных случаев известны только верхние и нижние оценки числа избыточных элементов. Так граница Варшамова-Гильберта определяет нижнюю границу для числа проверочных разрядов:
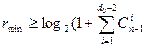 (4.24)
(4.24)
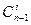 - число сочетаний из n-1 элементов по i элементам.
- число сочетаний из n-1 элементов по i элементам.
Граница Плоткина даёт верхнюю границу кодового расстояния 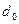 при заданном числе информационных (K) и общем (n) числе разрядов в КК:
при заданном числе информационных (K) и общем (n) числе разрядов в КК:
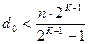 (4.25)
(4.25)
Использование пропускной способности дискретного канала связи для корректирующих кодов определяется избыточностью 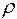 данного кода. Используя выражение (4.22) и границы для определения r можно построить следующий качественный график (рис 4.7)
данного кода. Используя выражение (4.22) и границы для определения r можно построить следующий качественный график (рис 4.7)
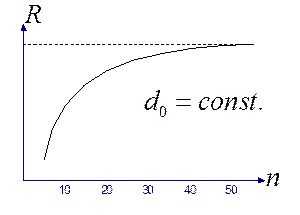
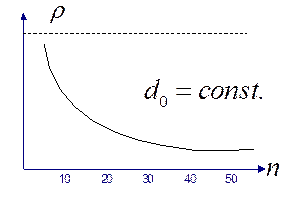
рис 4.7
Из (4.22) следует, что увеличение избыточности приводит к уменьшению скорости кода и худшему использованию пропускной способности канала связи. Однако, увеличение длины «n» КК уменьшает относительную избыточность и улучшает использование дискретного канала. Поэтому при использовании корректирующих кодов стремятся применять, возможно, более длинные КК.
Как мы уже отмечали в настоящее время разработано огромное количество разнообразных кодов. Рассмотрим классификацию помехоустойчивых кодов
(рис. 4.8).
Помехоустойчивые коды делятся на блочные и непрерывные.Непрерывные коды представляют собой непрерывные последовательности единичных элементов,не разделенных на блоки. В таких кодах избыточные разряды помещаются в определенном порядке между информационными. Типичным представителем непрерывных кодов являются рекуррентные или сверхточные коды.
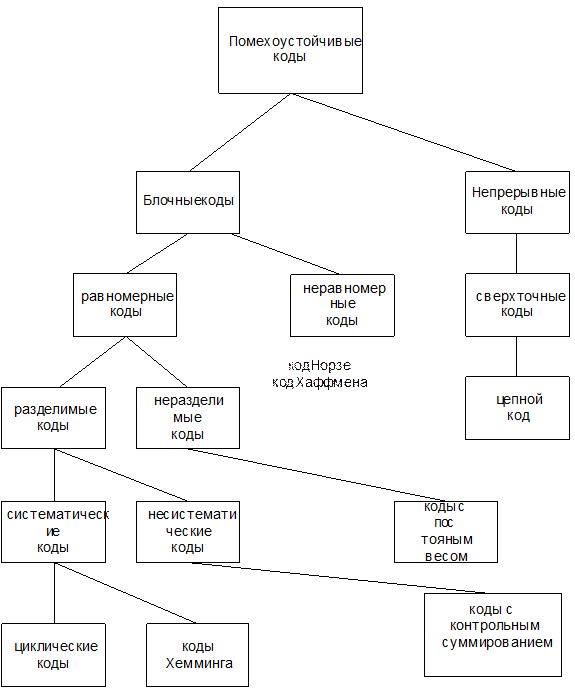
Рис 4.8
К блочным относятся коды, в которых каждому сообщению и знаку сообщения соответствует блок (КК) из «n» единичных элементов или блоки с разным числом разрядов. В этой связи блочные коды делятся на равномерные и неравномерные.
К неравномерным кодам относятся, например, код Морзе, у которого КК имеют разную длину (число разрядов). На практике наибольшее применение нашли равномерные коды, как наиболее просто технически реализуемые.
Равномерные блочные коды делятся на разделимые и неразделимые.
В разделимых кодах КК состоит из информационных проверочных разрядов, причем эти разряды стоят на определенных местах.
В неразделимых кодах деление на информационные и проверочные разряды отсутствует.
К таким кодам относятся коды с постоянным весом, например, код МТК-3 –семиразрядный код с весом КК равным 3. Сложность реализации.
Разделимые коды в свою очередь делятся на систематические (линейные) и несистематические (нелинейные).
Систематическими называются такие блочные разделимые (n,k) –коды, в которых k –разрядов (обычно первые) представляют собой комбинацию простого кода, а последующие (n-k) разрядов являются проверочными. Проверочные разряды образуются с помощью линейных операций над информационными разрядами.
Нелинейные коды указанным свойством не обладают. Примером несистематического кода является код с контрольным суммированием (проверка на четность или нечетность). В этом коде проверочные разряды записываются в виде суммы по модулю 2 (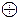 ) единиц в КК. Так в коде МТК-5 8-й разряд есть результат проверки на четность (нечетность) предыдущих семи разрядов.
) единиц в КК. Так в коде МТК-5 8-й разряд есть результат проверки на четность (нечетность) предыдущих семи разрядов.
К несистематическим кодам относятся. как уже отмечалось, коды с постоянным весом - это неразделимые коды. Однако они сложны в технической реализации. Хорош для ассиметричных каналов. Другим представителем несимметричных кодов являются коды Бергера. Они разделимые. Минимальное кодовое расстояние 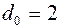 . Существует ряд вариантов построения этих кодов:
. Существует ряд вариантов построения этих кодов:
- подсчитывается число единиц в информационной части КК и это число в двоичном коде записывается в качестве проверочных разрядов;
- проверка на четность (нечетность) – добавляется один разряд, который дополняет КК до четной (нечетной).
1. Сумма по модулю 2 двух или нескольких разрешенных кодовых комбинаций
также является разрешенной кодовой комбинацией.
2. Минимальное кодовое расстояние равно минимальному весу его разрешенных КК.
3. При заданном минимальном кодовом расстоянии все КК имеют одинаковую длину – равномерность.
На практике широкое распространение получили именно систематические коды.
Различают два метода формирования проверочных разрядов:
- поэлементный
- в целом
Поэлементный способ - формирования проверочных разрядов применяется в кодах Хемминга. Обработка КК целиком для получения проверочной группы разрядов используется в полиномиальных кодах. Циклические коды являются разновидностью этого класса кодов.
Коды Хемминга относятся к линейным, групповым, систематическим кодам с 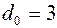 и
и
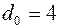 , в которых проверочные разряды формируются линейным преобразованием информационных разрядов поэлементным способом.
, в которых проверочные разряды формируются линейным преобразованием информационных разрядов поэлементным способом.
Правило нахождения проверочных разрядов является основной задачей построения корректирующих кодов. Рассмотрим этот процесс для кода Хемминга. Сначала познакомимся с понятием синдром кода.
Обнаружение и исправление ошибок избыточными кодами сводится к определению и последующему анализу синдрома.
Под синдромом понимают совокупность элементов, сформированных суммированием по модулю 2 принятых проверочных элементов и вычисленных проверочных элементов и вычисленных проверочных элементов по принятым информационным элементам с использованием одного и того же правила на передаче и приеме.
Если синдром нулевой, то ошибок в принятой КК нет. либо они не обнаружены. Наличие единиц в синдроме указывает на ошибку в принятой КК. Код Хемминга с 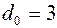 может исправить одну ошибку, поэтому синдром должен указать номер позиции в КК, где произошла ошибка. Этого достаточно для исправления ошибки в двоичных кодах.
может исправить одну ошибку, поэтому синдром должен указать номер позиции в КК, где произошла ошибка. Этого достаточно для исправления ошибки в двоичных кодах.
Постараемся таким образом сформировать проверочные разряды, чтобы синдром в двоичном коде указывал номер искаженного разряда в КК.
Рассмотрим пример построения кода с К=5, способным исправлять 1 кратную ошибку.
Пример: Дано К=5; 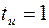 .
.
1. Определяем 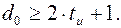 при
при 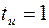 , с
, с 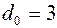 .
.
2. Определяем необходимое число проверочных разрядов, поскольку 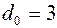 , то
, то 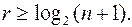
Это неравенство решается методом подбора:
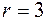 -----
-----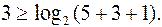 - не выполняется.
- не выполняется.
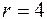 -----
-----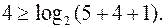 - выполняется.
- выполняется.
Таким образом,  и код имеет вид (9.5).
и код имеет вид (9.5).
Обозначим КК в виде:
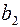
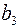
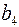
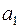
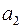
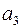
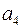
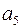
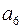
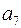
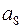
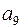 (1)
(1)
Составим таблицу возможных синдромов, определяющих номер разряда, где произошла ошибка. Т.к. разрядов 4, то синдром будет состоять из 4-х разрядов.
| Двоичная запись этого номера | |||||
| С4 | С3 | С2 | С1 | ||
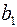
| |||||
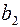
| |||||
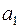
| |||||
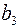
| |||||
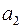
| |||||
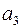
| |||||
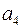
| |||||
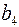
| |||||
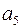
|
В алгоритме первой проверки введем те элементы, двоичные номера которых содержат в младшем разряде единицу. Из таблицы следует, что это элементы 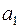 ,
, 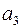 ,
, 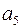 ,
, 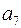 ,
, 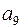 .
.
Аналогично, в алгоритм второй проверки включили те элементы, двоичные коды номеров которых содержат во 2-ом разряде единицу.
Аналогично для 3-ей и 4-ой проверок.
Обозначим результат каждой проверки как П1.Если П1=1. то это означает, что один из элементов КК, охватываемых первой проверкой, искажен. Наличие 1 в младшем разряде синдрома С1 указывает, что искомой искаженный элемент является нечетным, т.к. единицу в первом разряде имеют все нечетные числа. Следовательно, они и должны охватываться первой проверкой:
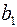

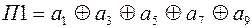 ;
; 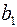 =
=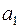
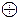
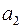
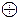
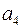
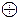
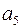 ; (4.26)
; (4.26)
Результат второй проверки П2 определяет второй разряд синдрома, т.е.
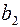
 |
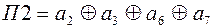 (4.27)
(4.27)
Далее:

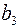
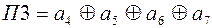 (4.28)
(4.28)

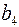
(4.29)
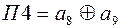
Теперь определим, какие позиции в КК занимают проверочные разряды, а какие информационные. Признаком проверочного элемента является то, что он входит только в один алгоритм проверки. При этом необходимо учесть. что в каждую проверку проверочный элемент должен входить только один раз.
Анализируя уравнения проверок видим, что элемент 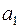 , входит только в первую проверку;
, входит только в первую проверку;
элемент 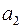 входит только во вторую проверку;
входит только во вторую проверку;
элемент 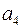 входит только в третью проверку;
входит только в третью проверку;
элемент 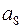 входит только в четвертую проверку.
входит только в четвертую проверку.
Поэтому уравнения проверок можно переписать в виде:

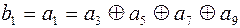
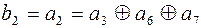
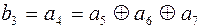
(4.30)
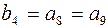
В дискретный канал передается следующая КК:
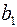
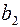
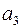
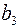
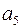
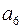
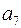
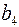
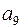
на приеме производится аналогичные проверки (4.31)
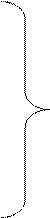
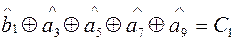 ;
;
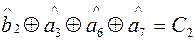 ;
;
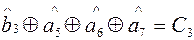 ;
;
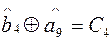 ; (4.31)
; (4.31)
Крышечки у символов означают оценки единичных элементов в месте приема. По виду синдрома определяют номер разряда, где произошла ошибка.
В классическом коде Хемминга проверочные элементы располагаются на 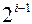 позициях, где i- номер проверочного разряда. При такой структуре КК усложняется аппаратура кодера и декодера. Поэтому на практике пользуются модифицированным кодом Хемминга, в котором изменяют, порядок передачи элементов КК в канал. Сначала передают информационные элементы, а затем проверочные.
позициях, где i- номер проверочного разряда. При такой структуре КК усложняется аппаратура кодера и декодера. Поэтому на практике пользуются модифицированным кодом Хемминга, в котором изменяют, порядок передачи элементов КК в канал. Сначала передают информационные элементы, а затем проверочные.
Классический код Хемминга
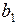
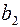
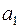
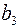
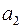
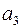
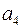
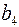
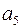





 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
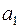
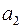
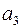
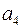
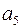
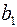
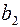
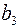
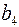 Модифицированный код
Модифицированный код
Проверка: 
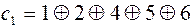

 вместо
вместо 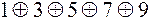
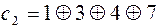 вместо
вместо 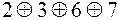
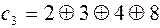 вместо
вместо 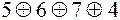
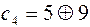 вместо
вместо 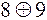
а на передаче проверки запишутся в виде:
Модифицированный код: Классический код:
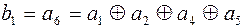
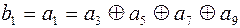
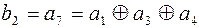
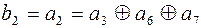
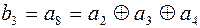
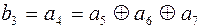
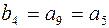
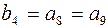
 2014-02-24
2014-02-24 3488
3488








