Процесс, протекающий при постоянном давлении, называется изобарным.
1. Условие процесса 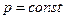 .
.
Из уравнения состояния 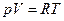 получим уравнение процесса
получим уравнение процесса
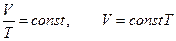 (5)
(5)
2. В координатах 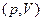 процесс изображается прямой называемой изобарой: 1-2 – изобара расширения, тепло подводится; 2-1 – изобара сжатия, тепло отводится.
процесс изображается прямой называемой изобарой: 1-2 – изобара расширения, тепло подводится; 2-1 – изобара сжатия, тепло отводится.
3. Соотношение между параметрами находится из уравнения процесса
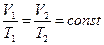 или
или 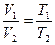 (6)
(6)
Изменение объема в изобарном процессе прямо пропорционально изменению абсолютной температуры.

| 4. Изменение внутренней энергии равно
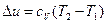 (7)
Количество теплоты, подведенное (отведенное) газу с учетом того, что теплоемкость равна (7)
Количество теплоты, подведенное (отведенное) газу с учетом того, что теплоемкость равна 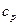 , можно подсчитать по формуле , можно подсчитать по формуле
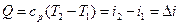 , (8) , (8)
|
| Рис.2. |
где 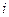 - энтальпия.
- энтальпия.
Количество теплоты, подведенное (отведенное) газу в изобарном процессе идет на изменение его энтальпии.
Работа будет равна
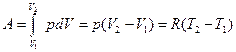 (9)
(9)
 2014-02-09
2014-02-09 555
555







