Принцип неопределенности для сигнала
Рассмотрим спектры некоторых сигналов.
Определим аналитически прямоугольный импульс следующим образом:

где А – амплитуда импульса;
t - длительность импульса (рисунок 16).
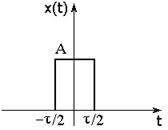
Рисунок 5 – Прямоугольный импульс
По общей формуле прямого интегрального преобразования Фурье (5) для спектра прямоугольного импульса получим:
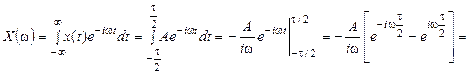
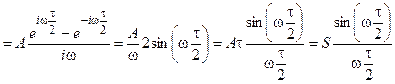 , (6)
, (6)
где  - площадь импульса.
- площадь импульса.
Для построения графика спектра (рисунок 6) рассмотрим несколько частных случаев:
1) при  , в силу свойства предела
, в силу свойства предела 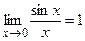 ;
;
2) нули функции 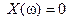 определятся из условия:
определятся из условия:
 ,
,
откуда
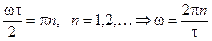 ;
;
3) при 
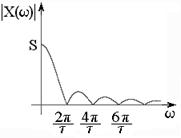
Рисунок 7 – Спектр прямоугольного импульса
Рассмотрим произведение 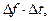 где
где 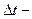 длительность импульса,
длительность импульса,  ширина спектра (f - циклическая частота). Длительность прямоугольного импульса определена и равна
ширина спектра (f - циклическая частота). Длительность прямоугольного импульса определена и равна 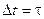 . Что же касается спектра, то он безграничен, хотя спектральная плотность убывает с ростом частоты.
. Что же касается спектра, то он безграничен, хотя спектральная плотность убывает с ростом частоты.
Будем считать (произвольно), что верхней границей спектра, определяющей его ширину, является частота, при которой спектральная функция первый раз обращается в нуль, то есть  . Ширина спектра равна разности частот:
. Ширина спектра равна разности частот:
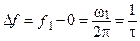 ,
,
откуда  .
.
Таким образом, произведение ширины спектра прямоугольного импульса на его длительность есть величина постоянная, равная единице.
Дельта–функция
Аналитически дельта–функция определяется в виде:

Осуществить переход от прямоугольного импульса к дельта–функции возможно при выполнении следующих условий:
 .
.
Действительно, при  амплитуда импульса А будет стремиться к бесконечности, однако его площадь, согласно свойству дельта–функции (1), останется величиной постоянной:
амплитуда импульса А будет стремиться к бесконечности, однако его площадь, согласно свойству дельта–функции (1), останется величиной постоянной:
 .
.
Спектр дельта–функции, в соответствии с (28), равен:
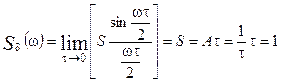 ,
,
то есть дельта–функция имеет равномерный единичный спектр на всех частотах (рисунок 8). Такой спектр по аналогии с белым светом называют «белым».

Рисунок 8 – Белый спектр
Интересно проследить деформацию спектра прямоугольного импульса при уменьшении его длительности. При  спектральная функция становится все более пологой и в пределе стремится к единичному значению (рисунок 9).
спектральная функция становится все более пологой и в пределе стремится к единичному значению (рисунок 9).
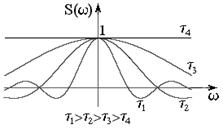
Рисунок 9 – Деформация спектра
Найдем для дельта–функции произведение  . Длительность ее известна
. Длительность ее известна 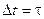 и стремится к нулю. Наибольшей будем считать частоту, при которой
и стремится к нулю. Наибольшей будем считать частоту, при которой  , то есть:
, то есть:
 ,
,
откуда 
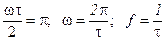 . Естественно, что при
. Естественно, что при  .
.
В результате 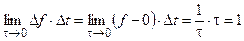 . Вновь получили константу, несмотря на то, что спектр по частоте безграничен.
. Вновь получили константу, несмотря на то, что спектр по частоте безграничен.
 2014-02-24
2014-02-24 4273
4273