Гипергеометрическое распределение

Гипергеометрическое распределение играет важную роль в области статистического контроля качества.

Будем говорить, что дискретная случайная величина Х, принимающая целочисленные значения X ={0,1,2,…, n }, распределена по гипергеометрическому закону, если вероятности этих значений определяются выражением

,

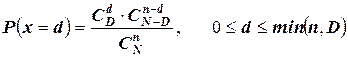где N – объём партии изделий;

n – объём выборки из данной партии изделий;

D – число дефектных изделий в данной партии изделий;

d – число дефектных изделий в соответствующей выборке изделий.

Свойства гипергеометрического распределения:

1. 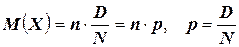(доказать самостоятельно);

2. 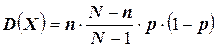(доказать самостоятельно);

3. при 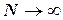гипергеометрическое распределение приближается к биномиальному распределению (о котором поговорим немного позднее).

ПРИМЕР 3. Партия из 100 изделий содержит 10% брака. Для контроля выбрано 5 изделий. Необходимо определить вероятность того, что в выборке меньше двух бракованных изделий. Найти 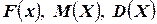для случайной величины Х – числа дефектных изделий в данной выборке изделий.

Решение. Данная дискретная случайная величина Х ={0,1,2,3,4,5}очевидно подчиняется гипергеометрическому закону распределения вероятностей. В нашем случае N = 100, D = 10, n = 5. Вероятность того, что в выборке ровно d бракованных изделий равна

.

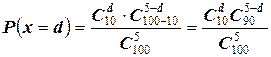Вычислим (приближённо) значения 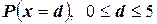и запишем их в таблицу

Х
р	0,583	0,340	0,070	0,007	0,000	0,000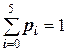

Найдём функцию распределения:

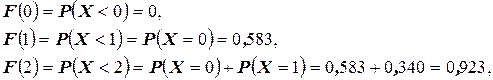
Аналогично найдём

.

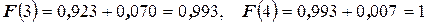Заметим, что 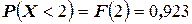. То есть вероятность того, что в выборке меньше двух бракованных изделий равна 0,923.

Далее, найдём

.

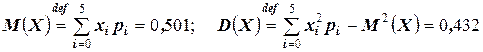Замечание: Сравним полученные значения математического ожидания и дисперсии с соответствующими значениями (см. свойства гипергеометрического распределения):

,

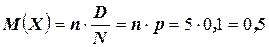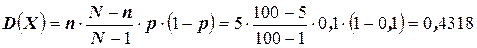
Как видим, не доказывая формулы для M (X)и D (X), на примере мы убедились в их справедливости.