Напомним, что обратимыми матрицами (мы рассматриваем квадратные матрицы размером n´n над полем F) мы называем те матрицы А, которые имеют левую или правую обратные матрицы, т.е такие матрицы В или С, что ВА=Е или АС=Е, где 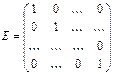 . Невырожденными матрицами мы называем матрицы А, чей ранг максимален: RangA=n. Соответственно, все остальные, чей ранг меньше n, называются вырожденными. Иначе говоря, векторы-строки невырожденных матриц (а, следовательно, по теореме о ранге матрицы, и векторы-столбцы) линейно независимы.
. Невырожденными матрицами мы называем матрицы А, чей ранг максимален: RangA=n. Соответственно, все остальные, чей ранг меньше n, называются вырожденными. Иначе говоря, векторы-строки невырожденных матриц (а, следовательно, по теореме о ранге матрицы, и векторы-столбцы) линейно независимы.
Следующее утверждение устанавливает, что если матрица имеет себе обратную с одной стороны (например, слева), то она имеет её же и с другой стороны (несмотря на некоммутативность умножения в кольце матриц).
1.1. Если ВА=Е, то и АВ=Е.
Во-первых, ввиду изоморфизма матриц n´n над полем F и линейных операторов (линейных преобразований векторного n-мерного пространства) n-мерного линейного пространства V (над полем F) с фиксированным базисом, это означает В(А(Х))=Х "ХÎV, а, значит, ImA=V, ибо никакой оператор (В) не может увеличить размерность пространства (максимального числа линейно независимых векторов в нём). Отсюда сразу следует, что kerA=kerB=0.
С другой стороны, Е коммутирует со всеми матрицами, так что ВЕ=ЕВ. Поскольку ВА=Е, то отсюда В(ВА)=(ВА)В=В(АВ); В(ВА-АВ)=0ÞВА-АВ=0ÞВА=АВ=Е.
Мы не могли непосредственно применить здесь упражнение 25 из конспекта «Введение в теорию групп», ибо там содержалось требование, чтобы у всех элементов существовали правые обратные. У нас же, во-первых, не все матрицы вообще обратимы, а во-вторых, априори (заранее) могло бы быть так, что некоторые матрицы обратимы только слева, а другие – только справа.
Как следствие, из только что доказанной теоремы получаем: множество всех обратимых матриц порядка n´n над полем F образует группу (по умножению). Эта группа обозначается как GL(n,F) и называется полной линейной группой.
Если матрица A=(ai,j) вырождена, и, если рассматривать её столбцы, как векторы – образы векторов стандартного базиса e1 =(1,0,0,…0); e2 =(0,1,0,0,…0); …; en =(0,0,…0,1), то она станет матрицей линейного оператора, который перевёл всё пространство V в некоторое его собственное подпространство и потому обратного оператора иметь не может (вернуть полученную систему линейно зависимых векторов в исходный базис не удастся ввиду леммы «о двух системах векторов»). С другой стороны, если она невырождена, то соответствующий ей линейный оператор перевёл стандартный базис е=(e1, e2,…,en) в некоторый базис f=(f1, f2,…,fn) и потому имеет обратный оператор, который однозначно определён тем, что «возвращает» вектора нового базиса обратно на место: A-1: f ® e. Значит, и сама матрица обратима. Итак, множество всех обратимых матриц совпадает с множеством всех невырожденных матриц.
Будем рассматривать теперь только невырожденные матрицы.
1.2. Поставим вопрос: какова должна быть матрица Bi,j(l), чтобы в результате её умножения слева на матрицу А к элементам i-ой строки матрицы А прибавлялись бы элементы j-ой строки, умноженные на l. Легко находим, что этой матрицей должна быть матрица
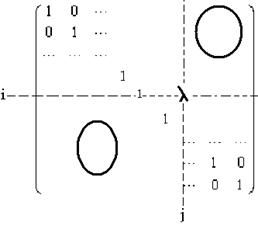
В частности, Bi,j(l)Bi,j(m)=Bi,j(l+m), откуда, между прочим, следует, что при фиксированных индексах i и j матрицы Bi,j(l) образуют группу (по умножению), изоморфную аддитивной группе поля F.
Матрицы, которые могут быть записаны как произведения нескольких матриц Bi,j(l) при всевозможных i ¹j и lÎF образуют группу SL(n,F) называемую унимодулярной группой. Упражнение 0. Почему они образуют группу?
Говорят, что элементарные матрицы Bi,j(l), i¹j порождают унимодулярную группу.
Наша цель – подобрать к данной невырожденной матрице А такую унимодулярную матрицу В, чтобы при умножении её слева на матрицу А получилась матрица как можно более простого вида. Поскольку А невырождена, в первом столбце найдётся ¹0 элемент. Поэтому можно умножением на элементарную матрицу B2,j(l) добиться того, чтобы a2,1¹0. После этого нетрудно добиться того, чтобы a1,1=1.
Упражнение 1.
На какую элементарную матрицу В1,2(*) надо для этого умножить слева матрицу А?
Добившись этого, мы затем легко добьемся того, чтобы в первом столбце матрицы А все остальные элементы стали равными нулю и матрица приобрела следующий вид: 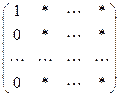 Упражнение 2. Что надо для этого делать?
Упражнение 2. Что надо для этого делать?
Теперь перейдем ко второму столбцу и спустимся на строку вниз:
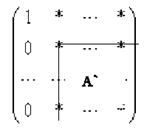
В отмеченной подматрице A` в первом столбце должны иметься ненулевые элементы. Упражнение 3. Почему?
Поэтому можно устроить (естественно, умножением слева на элементарную матрицу!) так, чтобы a3,2¹0. А уж после этого, тем же приёмом, что и выше, сделать a2,2=1. Сделав это, мы снова все остальные элементы второго столбца (включая и a1,2) умножениями на подходящие элементарные матрицы обнуляем: 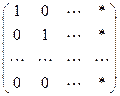 .
.
Продолжая в том же духе, мы, в конце концов, придём к матрице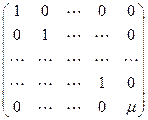 .
.
 2014-02-24
2014-02-24 473
473