Ортогонализация Грама-Шмидта

Упражнение 81.

Упражнение 80.

Упражнение 78.

Упражнение 77.

Упражнение 76.

Упражнение 74.

Упражнение 73.

Упражнение 72.

Упражнение 71.

Упражнение 59.

Упражнение 58.

Упражнение 57.

Упражнение 54.

Упражнение 53.

Упражнение 52.

Упражнение 51.

Установите изоморфизм между линейными отображениями ЛП V над F в сопряжённое к нему линейное пространство (ЛП) V*, y: V®V*, и билинейными формами j: V´V®F.

Определим новое отображение 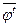: 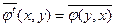. Проверьте, что новое отображение также 1,5 линейно. Проверьте, что, если все отображения записаны матрицами в одном и том же базисе, то операциям j®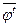и, в билинейном случае, j®j^t, соответствуют матричные преобразования А®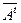и А®А^t соответственно.

Def. Билинейные j: V´V®F, такие, что j=j^t, называются симметричными, а также симметрическими. Они задаются симметричными матрицами Грама, а соответствующие им геометрии называются ортогональными.
Билинейные j: V´V®F, такие, что j=-j^t, называются антисимметричными, или кососимметрическими, или симплектическими. Им соответствуют антисимметричные матрицы Грама, а геометрии, ими определяемые, называются симплектическими.
Наконец, 1,5-линейные формы j такие, что j=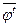называются эрмитовыми, равно, как и порождаемые им геометрии.

Как обычно, векторы х и у называются ортогональными, если j(х,у)=0. Соответственно, подпространства V₁ÍV и V₂ÍV называются ортогональными, если j(х,у)=0"хÎV₁,уÎV₂.

Ядром (kerj) формы j на V называется подпространство (кстати, почему это множество будет именно таковым?) тех векторов V, которые ортогональны всему V.

Форма называется невырожденной, если её ядро тривиально: kerj=0.

На множестве обратимых матриц определены три операции: транспонирования А®^tА, сопряжения А®`А и взятия обратной матрицы А®А^-1. Все ли они коммутируют (перестановочны) друг с другом? Первые две операции определены на любых прямоугольных матрицах m´n. Верно ли, что они и на них коммутируют?

Проверьте, что отношение ортогональности для векторов и для подпространств симметрично для симметрических, симплектических и эрмитовых форм. Обратное утверждение отнюдь не столь тривиально, в чём вы скоро убедитесь.
Проверьте, что невырожденность формы j равносильна, как невырожденности её матрицы Грама (в любом базисе), так и изоморфизму индуцированного ею линейного отображения j*: V®V* (см. упр.52). Def. Рангом формы j называется dim Imj*, или, что одно и то же, ранг матрицы Грама формы j.

Def. Изометрией двух ЛП V₁ и V₂ над одним и тем же полем F, снабжённых формами j₁ и j₂ соответственно, называется линейный изоморфизм f: V₁®V₂, сохраняющий значения форм: j₂(f(x),f(y))=j₁(x,y) "x,yÎV₁. Если между двумя пространствами существует изометрия, то они называются изометричными.

Упражнение 55. Является ли изометрия отношением эквивалентности?

Def. Вектор называется изотропным, если он ортогонален самому себе, т.е., если j(х,х)=0.В следующей серии упражнений дана билинейная форма j: V´V®F, симметричная относительно ортогональности, т.е.j(х,у)=0Þj(у,х)=0.
Упражнение 56.

Рассмотрим тройку векторов x, y, z. Проверьте, что j(х, j(x,y) z -j(x,z) y)=0.

Выведите отсюда, что " x, y, zÎ V j(x,y)×j(z,x)= j(y,x)×j (x,z).

Выведите отсюда, что, если j(z,x)¹j(x,z), то вектора х и z изотропны.

Ещё раз докажите (мы это уже ранее доказывали), что если все вектора изотропны, то форма – кососимметрическая. Наша цель – доказать (от противного), что если наша билинейная форма не симметрическая, то она – кососимметрическая. Предположим, что на какой-то паре векторов симметричность нарушается: j(z,x)¹j(x,z). Пусть у – произвольный неизотропный вектор. Тогда он коммутирует со всеми векторами. Почему?

В условиях предыдущего упражнения расширьте данное неравенство ещё двумя: 0¹j(z,x)¹j(x,z)¹0. Докажите, что вектор у ортогонален обоим векторам, х и z.

А теперь проверьте, что j(y+z,x)¹j(x,y+z). Выведите отсюда, что вектор у всё-такиизотропен (противоречие). Итак, вами доказано утверждение, (почти) обратное к упр. 55:
Если некоторая билинейная форма симметрична относительно ортогональности т.е.j(х,у)=0Þj(у,х)=0, то она либо симметрическая, либо кососимметрическая.

Упражнение 60. Докажите, что любую билинейную форму можно разложить в сумму двух форм: симметрической и кососимметрической.

План нашего дальнейшего изучения 1,5 и 2-ЛФ таков: сначала посмотрим, что они собой представляют в маломерных случаях, а затем попробуем многомерные пространства разложить в прямую сумму маломерных, в которых поведение этих форм уже изучено. Собственно, таков общий принцип изучения и других объектов.

Поскольку свойства геометрий существенно разнятся, в зависимости от типов форм, проведём наше исследование отдельно для каждого случая.

А) V -ортогональное пространство, dimV=1.

Любой ненулевой вектор v порождает V, является его базисом, и симметрическая форма
j: V´V®F определяется её значением на v. Если j не тождественно нулевая, то j(v,v)=а¹0.Соответственно, для х= х v и у= у v j(х, у)=а²ху. Таким образом, на одномерных пространствах j не тождественно нулевая Û j невырожденная. Рассмотрим подмножество М мультипликативной группы F* обратимых элементов поля F (т.е. всех вообще, кроме нуля), состоящее из всех квадратов: mÎM Ûm=z², zÎF*.

Упражнение 61.
Докажите, что М – подгруппа (мультипликативная, естественно) группы F*.

Упражнение 62*.
Докажите, что существует биекция между смежными классами аМ и различными
(не изометричными) 1,5 и 2-ЛФ на одномерных ВП а именно:
Пусть dimV=dimW=1, V порождается вектором v, а W порождается вектором w (то есть, V=F v, W=F w) и j(v, v)=а, y(w, w)=b. Пусть, далее, M=(F*)².
Тогда aM=bM Û существует изометрия f: (V,j)®(W,y).

Для F=R M=(R*)²=R₊ - группа всех положительных вещественных чисел и
F*/ F*²={1,-1}. Для F=С M=(C*)²=C*; C*/ C*²={1}.

Поэтому существуют лишь три не изометричных одномерных ортогональных пространства над R, задаваемых в координатах произведениями ху, -ху и 0 и два не изометричных одномерных ортогональных пространства над С: задаваемых произведениями ху, и 0.
Как видите, ответ существенно зависит от свойств поля F: чем больше фактор-группа F/(F*)², тем больше неизоморфных одномерных ортогональных пространств. Скажем, исследование для случая F=Q уже могло бы стать темой вашей проектной работы.
В) V -эрмитово, dimV=1.
Упражнение 63*.

Проведите анализ этого случая самостоятельно, по аналогии с предыдущим. В качестве полезного совета рекомендуем убедиться, что значения эрмитовой j(v, v) вещественны " v.

Ответ будет такой же, как для симметрических билинейных форм над R: 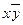; -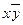и 0.

Для симплектических пространств придётся повысить размерность V до двух, ибо (по крайней мере, для R и С) любая кососимметрическая форма на одномерном пространстве тождественно равна нулю: все вектора в симплектических пространствах изотропны. Обратное этому утверждение вы уже доказывали (в том числе, в упр. 57).

Упражнение 64. Докажите это (утверждение, набранное курсивом).
Итак, С) V - симплектическое, dimV=2.
Упражнение 65.
Докажите, что(V,j) вырождено Þ j нулевая.
Пусть теперь j не нулевая, и, стало быть, невырожденная. Тогда

Упражнение 66.
В(V,j) найдётся базис (е₁, е₂) в котором матрица Грама формы j имеет вид: .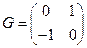

Итак,любое двумерное симплектическое пространство над R или над С изометрично пространству с формой, заданной в координатах выражением х₁у₂-х₂у₁ (или равной 0).
В общем-то, это верно для всех полей, кроме тех, в которых 2х=0 "х.

Переходим ко второму пункту программы: разложению в прямую сумму одномерных или двумерных подпространств. Напомним вначале некоторые определения.
Пусть имеем (V,j) и его подпространство WÍV. Ограничение j на W обладает всеми своими свойствами (остаётся билинейным, полуторалинейным, симметрическим, кососимметрическим или эрмитовым в зависимости от того, каковым оно было в V).

Назовём W невырожденным или, соответственно, изотропным, если ограничение j на W невырожденно или, наоборот, равно нулю. Ортогональным дополнением к W называется подпространство W^{^}ÍV, состоящее из всех векторов, ортогональных W: W^{^}={vÎV½j(v,w)=0 "wÎW}. А теперь откроем летний конспект «Vector Spaces-I» на стр.10 и сверим терминологию. Там билинейная форма задавалась над разными (более общая ситуация) ВП, V и W, (но над одним и тем же полем К) и обозначалась как á*,*ñ.

У нас же либо W=V, либо W=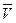(в эрмитовом случае; 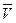означает, что поле С комплексных чисел, над которым V есть ВП, снабжено автоморфизмом a®`a, так что a v ®`a v), и форма обозначается как j(*,*).

Пусть теперь на V задана билинейная или 1,5 линейная форма и W –подпространство V, WÍV. Глядя на упражнения №№53-56 (и, особенно, на №56), переобозначая в соответствии с задачей названия ВП, и рассмотрев сужение формы на W, т.е., рассмотрев билинейную форму на W´V (или на W´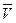) показать, что всегда, когда V конечномерно, то

Упражнение 67.
W+W^{^}=V. Если же форма невырождена на W, то V=WÅ W^{^}.
А если ещё она к тому же и на W^{^} невырождена, то (W^{^})^{^}=W.
Упражнение 68.

Приведите примеры, когда
а) форма на V вырождена, а на WÍV – невырождена и когда
б) форма на V невырождена, а на WÍV – не то, что вырождена, а вообще – нулевая!

Упражнение 67 открывает двери для доказательства индукцией по dimV следующей важной теоремы:
Упражнение 69*.
ПустьV - конечномерно, ортогональное, симплектическое или эрмитово.
Тогда его можно разложить в прямую сумму V=V₁Å V₂Å …ÅV_n, (12)

попарно ортогональных подпространств, одномерных в ортогональном и эрмитовом случае и вырожденных одномерных или невырожденных двумерных в симплектическом случае.
Единственный тонкий момент здесь встречается лишь в эрмитовом случае, где из допущения, что j(v,v)=0 "vÎV не следует сразу, что форма нулевая, а следует лишь, что
0=j(v+w,v+w)=2Rej(v,w). То есть, форма принимает лишь чисто мнимые значения: j(v,w)=ir, где rÎR. Но тогда, допустив, что r¹0, придите к противоречию, рассмотрев значение эрмитовой формы на векторах (ir)^-1 v и w.

Пусть мы имеем (V,j), V₀=kerj, dimV=n, dimV₀=n₀. Если форма j симметрическая над F=R или эрмитова над F=C, то введём ещё два целых неотрицательных числа: n₊ и n_- - числа одномерных подпространств в некотором разложении V, на которых j соответственно положительна или отрицательна в соответствии с упражнениями 62, 63 и 69.

Мы хотим убедиться в том, что эти числа – инварианты (V,j) и не зависят от разложения V. Серия упражнений №№ 73-77 призвана удостоверить вас в том, что в этих случаях набор (n₀,n₊,n_-), называемый сигнатурой определяет пространство с точностью до изометрии.

Упражнение 70.
Пусть (V,j) – эрмитово или ортогональное пространство над полем С.
Пусть 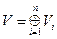- его разложение на одномерные, взаимно ортогональные подпространства, гарантированное упражнением-теоремой 69. Пусть V₀=kerj - ядро j, а W_r=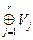- прямая сумма тех одномерных подпространств в этом разложении, на которых форма j вырождена. Очевидно, что W_rÍV₀. Докажите, что на самом деле W_r=V₀. (hint: assume the opposite.)
Тем самым будет доказано, что число n₀=dim kerj совпадает с числом одномерных подпространств в этом разложении, на которых форма j вырождена.

Пусть теперь (V,j) – симплектическое пространство над любым полем F (кроме тех, у которых х+х=0 "хÎF). Пусть снова 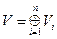- его разложение на взаимно ортогональные, одномерные вырожденные и двумерные невырожденные подпространства. Вновь, пусть V₀=kerj - ядро j, а W_r=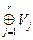- прямая сумма тех одномерных подпространств в этом разложении, на которых форма j вырождена. Докажите, что и в этом случае W_r=V₀.

Пусть теперь (V₁,j₁) и (V₂,j₂) – два пространства, либо оба симплектические над одним и тем же полем F, либо оба ортогональные над полем С. Докажите, что они изометричны Û размерности как самих пространств, так и ядер их 1,5-линейных форм одинаковы.

Итак, подводя итоги упражнений №№70-72, мы можем сказать:

Пусть пространство (V,j) – симплектическое над полем F, или ортогональное над полем С.
Пусть V₀=kerj, dimV=n, dimV₀=n₀. Тогда набор из двух целых неотрицательных чисел (n,n₀) определяет пространство (V,j) с точностью до изометрии.

Пусть теперь (V¹,j₁) и (V²,j₂) – два пространства, либо эрмитовых над С, либо ортогональных над R. Пусть их сигнатуры – 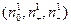и 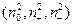в каких-то разложениях 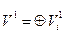и 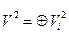. Допустим, что эти пространства изометричны.

Докажите, что тогда =.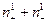

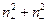Пусть 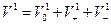; 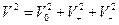- разложения этих пространств в суммы нулевых, положительных и отрицательных подпространств; f: V₁®V₂ – изометрия этих пространств, а 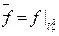- ограничение изометрии f на подпространство ; .

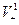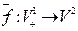Докажите, что подпространства 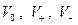линейно независимы: ни один ¹0 вектор одного из этих подпространств не может быть получен как сумма векторов других подпространств.
Допустим, что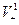 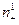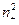dim=>=dim.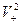

Упражнение 75^*.

Докажите, что тогда найдётся ненулевой вектор v Î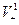в разложении образа которого в V², 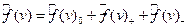составляющая .
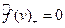(hint: composition of the and the projector is linear, though not isometric and so one can exploit the theorem about Im and Ker).

Выведите из результата предыдущего упражнения, что, всё-так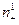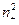и, =и =.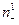

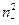Таким образом, мы доказали, что сигнатуры изометричных, эрмитовых над С или ортогональных над R пространств одинаковы. Докажите теперь и обратное утверждение:

Если сигнатуры пространств, эрмитовых над С или ортогональных над R совпадают, то между ними можно установить изометрию.

3.2. Def. Базис е=(e₁, e_2,…,e_n) в (V,j) называется ортогональным, если j(e_i,e_j)=0 при i¹j.

Ортогональный базис называется ортонормированным, если j(e_i,e_j)=0 или ±1.
Предыдущие упражнения показывают, что у любого ортогонального пространства над R или C и у любого эрмитова пространства имеются ортонормированные базисы.

Если (V,j) невырожденно и базис (e₁, e_2,…,e_n) ортогонален, то коэффициенты разложения любого вектора v по этому базису могут быть вычислены по формуле:
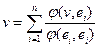(13)

В симплектическом случае мы обеспечены наличием симплектического базиса (e₁,e_2,…,e_k,e_k+1,…,e_2k,e_2k+1,…,e_n), для которого j(e_i,e_k+i)=-j(e_k+i,e_i)=1, i=1,2,…,k, а все остальные j(e_i,e_j)=0.
Упражнение 79.
Почему обеспечены? Как выглядят матрицы Грама в ортонормированных и в симплектических базисах? Каковы их ранги?
Почему невырожденное симплектическое пространство обязательно чётномерно?

Def. При х=у билинейная j(х,у) превращается в y(х)=j(х,х) и называется квадратичной формой. Итак, квадратичной формой называется такое y: V®F, для которого существует билинейная форма j: V´V®F, такая что y(х)=j(х,х) "хÎV.

Докажите, что " квадратичной y(х) $! симметрическая j(х,у) (называемая поляризацией y)
такая, что y(х)=j(х,х) "хÎV. (hint: just express j(х,у) through y(х), y(y) and y(х+y)). From this exercise one can easily see once more how to solve the ex. #60.

Поскольку, таким образом, установлена биекция между квадратичными и симметрическими билинейными формами, то ортогональные геометрии можно рассматривать как геометрии (V, y), где y(х) – квадратичная форма. Если х =х₁ е₁ + х₂ е₂ +…+ х_n е_n, тоy(х)=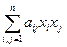, где а_ij=j(e_i,e_j)=а_ji. Теоремы классификации означают, что невырожденной линейной заменой переменных квадратичную форму можно привести к сумме квадратов y(х)=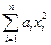, где а_i=0 или ±1. Числа k₀, k₊ и k_- нулей, единиц и -1 среди коэффициентов а_i определены однозначно и составляют сигнатуру исходной квадратичной формы; сумма k₊+k_- является её рангом.

До сих пор мы доказывали существование таких базисов для разных видов полуторалинейных форм, в которых они имеют наиболее простой, или, точнее, удобный вид. Мы не указывали, однако, никакого алгоритма нахождения такого базиса или замены переменных, приводящих, например, квадратичную форму к сумме квадратов. Сейчас мы займёмся такими процедурами.

Итак, мы имеем квадратичную форму y(х)=.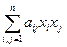
Случай А): имеется некоторый ненулевой коэффициент на диагонали матрицы (а_ij). Можем считать, что это а₁₁. Тогда y(х)= а₁₁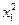+х₁(2а₁₂х₂+…+2а_1nx_n)+y₁(x₂,…,x_n). Выделяя полный квадрат и делая замену у₁=х₁+(а₁₂х₂+…+а_1nx_n):а₁₁; у₂=х₂;…;у_n=x_n, получим в новых переменных форму а₁₁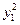+y₂(у₂,…,у_n). Далее применяем ту же процедуру к y₂(у₂,…,у_n).

Случай Б): все диагональные элементы матрицы (а_ij) нулевые.
Тогда, если нужно, перенумеровав переменные, будем иметь а₁₂¹0.
Тогда y(х)=2а₁₂х₁х₂ +х₁f₁(х₃…x_n)+х₂f₂(х₃…x_n))+y₃(x₃,…,x_n), где f₁ и f₂ – линейные, а y₃ - квадратичная. Введём новые переменные х₁=у₁+у₂; х₂=у₁-у₂; у₃=х₃;…;у_n=x_n.

Докажите, что этим мы сводим задачу вновь к случаю А). Покажите, что, действуя подобным образом, мы, в конце концов, приведём квадратичную форму к виду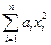. Проверьте, что по ходу дела все промежуточные замены переменных были линейными и невырожденными и, стало быть, такова же будет и результирующая замена переменных. Какова должна быть последняя замена переменных, приводящая форму в случае R к сумме квадратов с коэффициентами ±1, а в случае С – просто к сумме квадратов?
Какая матрица ей соответствует?

Опишем сейчас алгоритм ортогонализации («распрямления») произвольного базиса { e ₁, e ₂,…, e _n}, заданного в ортогональном или эрмитовом пространстве (V,j).

Пусть V_i – пространство, натянутое на вектора { e ₁, e ₂,…, e _i}, i=1,2,…,n или, иными словами, линейная оболочка независимых векторов { e ₁, e ₂,…, e _i}, V_i=L(e ₁, e ₂,…, e _i). Предположим, что не только всё V, но и все V_i невырождены. Будем строить новый, ортогональный базис { f ₁, f ₂,…, f _n} по индукции. Положим f ₁= e ₁; f ₂ будем искать в плоскости V₂={ f₁,e₂ }, т.е. как вектор f ₂= e ₂-x f ₁, ортогональный вектору f ₁. Найдём коэффициент х как решение уравнения j(e ₂-x f ₁, f ₁)=0.
Упражнение 82. Где мы использовали невырожденность V₁?
Почему вектора{ f ₁ ,f ₂} образуют базис того же V₂, так же, как и вектора { e ₁, e ₂}?

Упражнение 83 *.

Продолжите построение, сделав индуктивный шаг (переход от уже построенных ортогональных векторов { f ₁, f ₂,…, f _i-1} к вектору f _i).

Укажите места, где вы используете линейную независимость векторов { e ₁, e ₂,…, e _i} и невырожденность пространств V_i.

По существу, это – новое, уже конструктивное (то есть, указывающее алгоритм нахождения) доказательство существования ортогонального базиса.

Из только что проделанного построения и из упражнения 67 следует, что любой ортогональный базис невырожденного подпространства можно дополнить до ортогонального базиса всего пространства (ср. с «Vector Spaces-I», где мы доказывали, что любую линейно независимую систему векторов можно дополнить до базиса).

Пусть M_i – диагональные миноры матрицы Грама симметрической или эрмитовой j в исходном базисе { e ₁, e ₂,…, e _i}, M_i=(j(е_k,e_t)), 1£k,t£i.

Упражнение 84 *.

Сигнатура формы j определяется числом положительных и отрицательных элементов в последовательности detM₁, detM₂:detM₁; detM₃:detM₂;…;detM_n:detM_n-1.

Def. Форма j называется положительно определённой, если j(х,х)>0 "xÎV, x¹0.

Её матрицы Грама также называются положительно определёнными.
Из предыдущего упражнения вытекает, что j положительно определёна Û все её detM_i положительны (Критерий Сильвестра).

Упражнение 85 *. (теорема Якоби)

Любую квадратичную симметрическую форму j с невырожденными диагональными минорами M_i над любым полем F можно линейными преобразованиями переменных привести к виду 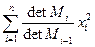, detM₀=1.

До сих пор мы пытались вести изучение разных видов пространств параллельно, отмечая их сходства и общие свойства. Всё-таки, между ними имеются и существенные отличия, и сейчас мы приступаем к их раздельному, последовательному изучению. Вначале займёмся классикой, тем, что и является предметом изучения в программе по геометрии средней общеобразовательной школы.

3.3. Евклидовы пространства.

Def. Симметрическая положительно определённая форма называется скалярным произведением. [2] Конечномерноевещественное линейное пространство E, в котором задано скалярное произведение, называется евклидовым.
Принято скалярное произведение обозначать скобками, т.е., вместо j(х,у) писать просто (х,у). Число 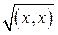называется длиной вектора х и обозначается ||х||.
Из самого определения скалярного произведения следует, что в евклидовом пространстве длина любого ненулевого вектора положительна, а длина нулевого вектора равна нулю. Из предыдущих упражнений вытекает, что в евклидовом пространстве всегда имеется ортонормальный базис, в котором скалярное произведение имеет вид (х,у)=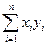. Таким образом, евклидово n-мерное пространство Е изометрично координатному пространству Rⁿ, в котором длины векторов вычисляются по теореме Пифагора. "х,уÎЕ рассмотрим величину ||lх+у||² как функцию от l. По определению скалярного произведения она всегда неотрицательна. Сделав отсюда вывод о дискриминанте квадратичной функции, докажите знаменитую теорему Коши-Буняковского[3]:

Упражнение 86.
"х,у ÎЕ (х,у)£||х||×||у||.
Из этого неравенства вытекают далеко идущие следствия.
Ну, во-первых, докажите, что
Упражнение 87. Равенство в нём достигается Û х и у линейно зависимы.
Во-вторых, докажите, что имеет место неравенство треугольника:
Упражнение 88. ||х+у||£||х||+||у||
Def. Векторное пространство V (на этот раз не обязательно конечномерное) над полями R или С называется нормированным, если на нём определена такая функция ||. ||: V®R₊ называемая нормой, что
а) || 0 || =0; || х || >0 "x¹0
b) || ax || =½a½× || x || и
с) || х+у || £ || х || + || у || "х,у.
Def. Множество М с заданной на нём вещественной функцией r: М´М®R₊, обладающей следующими свойствами:
а) r(х,у)=r(у,х) (симметрия)
б) r(х,х)=0; r(х,у)>0 Û x¹y (положительная определённость)
в) r(х,z) £r(х,y)+r(y,z)(неравенство треугольника)
называется метрическим пространством, а функция r - метрикой.
Её значение на паре точек (х,у) называется расстоянием между точками х и у.
Определение, как видите, отвечает нашему интуитивному представлению о расстоянии.
Упражнение 89.
Пусть у вас имеется нормированное пространство V. Превратите его в метрическое, задав, на базе его нормы ||. ||, расстояние между точками-векторами пространства V (напоминаю, что, если считать все вектора стрелками, исходящими из одной точки 0, то их концы находятся во взаимно-однозначном соответствии с точками аффинного пространства). Проверьте, чтобы ваша метрика была инвариантна относительно сдвигов (если это окажется не так, то она доброго слова не стоит): r(х, у)=r(х + z, y + z).
Таким образом, понятие метрического пространства шире понятия нормированного (всякое нормированное является метрическим).

Упражнение 90. (обратное к предыдущему)
Пусть наоборот, у вас имеется векторное пространство V и заданная на нём метрика, инвариантная относительно сдвигов: r(х, у)=r(х + z, y + z) " x, y,z + к тому же ещё обладающая свойством (гомотетия увеличивает расстояния): r(a х,a у)=½a½r(х, y).
Задайте на нём норму, на основе этой метрики, и проверьте, что все требования, предъявляемые к норме, действительно выполняются.
Упражнение 91.
Проверьте, что длина вектора, введённая в начале этого параграфа, является нормой.

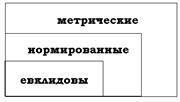Таким образом, евклидовы пространства являются нормированными.

Для нормированных и для метрических пространств естественным образом определяются шары и сферы (границы шаров). На них (с помощью шаров) легко переносятся понятия «близко – далеко». Ими мы плотно займёмся в следующем году.
А теперь рассмотрим величину .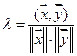
В силу упр.86 -1£l£1. Поэтому существует некий угол j, косинус которого равен как раз этому l: cosj=l. У нас уже имеется интуитивное понятие угла, чуть ли не с дошкольного возраста, а если бы и не было, то мы могли бы его сейчас определить таким образом. Вот есть два вектора, х и у в евклидовом пространстве.
С ними связана некая величина l, равная отношению их скалярного произведения к произведению их норм. Она (l) есть функция (cos) некоего аргумента (j), называемого углом между векторами х и у, определённая на промежутке 0£j£p таким образом, что cos0=1, cosp=-1, cos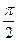=0. Иными словами, 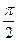– это угол между ортогональными векторами. Напротив, коллинеарны те и только те вектора, угол, между которыми составляет либо 0, либо p радиан.

Упражнение 92.
Докажите трёхмерный аналог теоремы Пифагора сначала обычными средствами: рассмотрением прямоугольного параллелепипеда и его главной диагонали (проекция и сведение к двумерному случаю), а затем её многомерного варианта прямо из данных выше определений: если векторы х₁, х₂,…,х_n попарно ортогональны, то квадрат их суммы (гипотенузы) равен их сумме квадратов (катетов):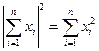. Проверьте также, что в тождество превращается и теорема косинусов.
С этого момента эстафетную палочку дальнейшего изучения евклидовой геометрии можно передать геометрии, прежде всего её давно обещанной «французской части».