Симплекс-метод в линейном программировании

Задачи линейного программирования удобно решать симплекс-методом – специальным методом оптимального (направленного) перехода. Он заключается в последовательном переходе от одной вершины области допустимых значений к другой, соседней, в которой значение функции цели лучше, чем в исходной точке. Движение происходит по периметру контура двумерной области или в случае более двух переменных – по ребрам многомерного многогранника. Более оптимальным, строго говоря, был бы путь не по периметру (или ребрам), а поперек области или вдоль грани, или внутри объема многогранника к оптимальной вершине.

Аналитически доказывается, что:

– экстремум в задачах линейного программирования – единственный, т.е. локальный экстремум одновременно является и глобальным и достигается на границе области допустимых значений, как правило, в вершине (при этом исключаются из рассмотрения особые случаи, в том числе случаи достижения экстремума на множестве точек, расположенных на ребре выпуклой области допустимых значений);

– симплекс-метод обеспечивает сходимость к экстремальной точке за конечное число шагов (конечность симплекс-метода), так как он предусматривает последовательный просмотр вершин многогранника, число которых конечно и (при определенных оговорках) является оптимальной процедурой отыскания экстремума.

Пусть исходная формулировка задачи содержит только положительные переменные и равенства, а не неравенства-равенства. Если этого нет, то изменением начала координат можно добиться положительности всех координат в допустимой области, а введением дополнительных положительных переменных свести неравенства к равенствам.

Геометрически (для случая n = 2) этот метод означает следующее. На первом шаге выбирают любую вершину многогранника и проводят через нее прямую – функцию цели. Решения (конкретные значения x₁, x₂), соответствующие вершине, будут опорными (базисными). По найденным значениям x₁, x₂ и функции цели находят направление к другой вершине (второй шаг), в которой функция цели возрастает (или убывает, если ищется минимум). В результате получают второе опорное решение. Симплекс-метод дает оптимальную последовательность шагов, приводящую к оптимальному решению, если оно существует.

Наглядная геометрическая интерпретация процесса нахождения оптимального решения получится, если от исходной прямоугольной системы координат (x₁, x₂) перейти к двумерной косоугольной системе введением дополнительных неосновных свободных переменных

y _v = x_{n+ v}, n = 1,..., m

в соответствии с равенством (2.3). Тогда для случая двух переменных имеем

y _v = a_v1x₁ + a _{v 2}x₂ + b _v.

В качестве преобразующих формул можно выбрать любые из соотношений (1.4). При этом в области допустимых значений y _v положительны. Из всего многообразия набора новых переменных следует выбрать такую систему координат, в которой бы новое начало координат у = = 0 совпадало с одной из вершин многогранника. В противном случае придется приближать новое начало координат к одной из вершин многогранника.

Пример. Максимизируем функцию

(2.7)

L = –4x₁ + x₂ = max

при ограничениях:

x₁ + 4x₂ – 8 ³ 0;

(2.8)

2x₁ – x₂ + 2 ³ 0;

–x₁ – x₂ + 10 ³ 0;

– x₁ + 2x₂ + 2 ³ 0.

Для этого перейдем от прямоугольной системы координат (x₁, x₂) к косоугольной (y₁, y₂) (рис. 2.5), для которой (система 1)

y₁ = –x₁ + 2x₂ + 2= x₃;

y₂ = x₁ + 4x₂ – 8 = x₄.

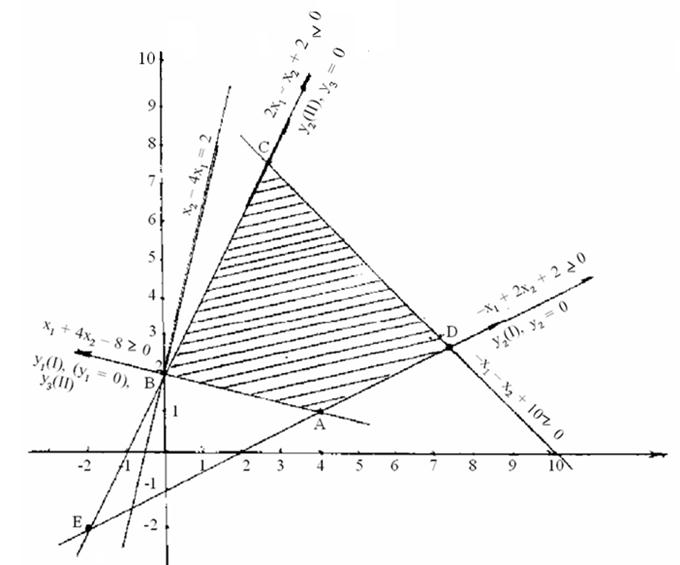
Рис. 2.5. Геометрическая интерпретация симплекс-метода для двумерного случая

В новой системе 1 осями координат будут прямые y₁ = 0, y₂ = 0, совпадающие с ребрами AD и АВ, начало координат совпадет с вершиной А, координаты которой x₁ = 4, x₂ = 1. Функция цели примет вид

L = –4x₁ + x₂ = 17/16y₁ – 7/6y₂ – 15,

так как

x₁ = – 2/3y₁ + 1/3y₂ + 4;

x₂ = 1/6y₁ + 1/6y₂ + 1.

В начале координат (точка A) y₁ = x₃ = 0; y₂ = x₂ = 0; L_A = –15. Функция цели возрастает при увеличении y₁ = x₃, поэтому следует двигаться в положительном направлении оси y₁ = x₃; y₂ = x₄ = = 0 и в вершине В перейти к новой системе координат (система 2):

y₂ = x₄ = x₁ + 4x₂ – 8;

y₃ =x₅ = 2x₁ – x₂ + 2

(точка пересечения прямых y₂ = 0, y₃ = 0 определяет вершину B). Выражая из формул (2.8) x₁ и x₂ через y₂, y₃, получаем:

x₁ = 1/9y₂ + 4/9y₃;

x₂ = 2/9y₂ – 1/9y₃ + 2.

Подставляя эти выражения в линейную форму (2.7), имеем

L = –4x₁ + x₂ = –2/9y₂ – 2y₃ + 2.

Отсюда значение функции цели в вершине B L_B = +2.

Поскольку оба коэффициента при линейной форме отрицательны, увеличивать ее значение, оставаясь в пределах ограничений (2.8) (т.е. внутри многоугольника ABCD), больше невозможно – максимум достигнут.

Заметим, что на рис. 2.5 граница области соответствует прямым у_i = 0 (i = 1, 2, 3, 4). Нумерация всей косоугольной системы координат меняется на каждом шаге. Так, на первом шаге прямая AD является осью у₂, а прямая АВ – осью у₁; на втором шаге прямая АВ является осью у₃, а прямая ВС – осью у₂. Косоугольная система координат будет выбрана неудачно, если:

y₁ = –x₁ + 2x₂ + 2 = x₃;

y₃ = 2x₁ – x₂ + 2 = x₅.

В этом случае начало координат (y₁ = x₃ = 0, y₃ = x₅ = 0) придется на точку Е с координатами x₁ = –1,5, x₂= –2, не принадлежащую области допустимых значений. Общее правило выбора начальной вершины заключается в том, что она должна лежать на пересечении пары осей косоугольных координат у_i = 0 (i= 1, 2,..., m) и при подстановке ее координат в другие ограничения остальные координаты у_j должны быть положительны, т.е. точка должна принадлежать допустимой области.

При большом числе переменных геометрическая интерпретация не так удобна, и целесообразно найти аналитический алгоритм определения оптимального решения.

В симплекс-методе, как это показано на примере, признаком движения вдоль грани является положительность знака коэффициента линейной функции цели, выраженной через косоугольные координаты. Двигаться к очередной вершине следует в положительном направлении той косоугольной координаты у_i, при которой коэффициент положителен, причем в случае многих переменных

L = c₁y₁ + c₂y₂ +... + c_my_m

этот коэффициент должен быть наибольшим. При многих переменных геометрическая интерпретация симплекс-метода с помощью косоугольной системы координат сохраняет свою силу, только число координат должно быть равно числу ребер, исходящих из данной вершины (рис. 2.6). Далее заметим, что косоугольные координаты y_i совпадают с дополнительными переменными x_n+i, которые вводятся для того, чтобы ограничения-неравенства перевести в строгие равенства.

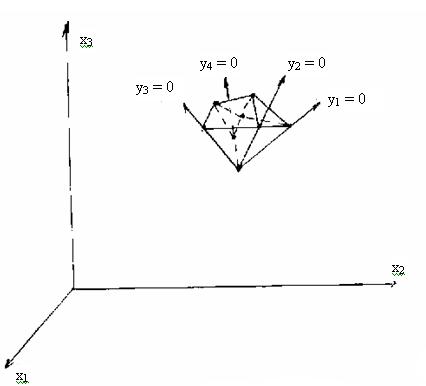
Рис. 2.6. Геометрическая интерпретация симплекс-метода для трехмерного случая

Рассмотрим рис. 2.7, на котором представлена область допустимых значений на плоскости (x₁,x₂) и поверхность функции цели L(x₁,x₂). Так как ограничения линейные, то допустимая область представляет собой выпуклый многоугольник. Из-за линейности функции цели

L(x₁,x₂) = c₁x₁ + c₂x₂ + b

поверхность ее является плоскостью в трехмерном пространстве, наклонной к горизонтальной плоскости (x₁,x₂) под определенным углом. Граница области допустимых значений через функцию цели отобразится в некоторый многоугольник в плоскости L(x₁,x₂). Нетрудно с помощью геометрического воображения убедиться, что экстремум совпадает с одной из вершин этого многоугольника и он – единственный. В исключительном случае экстремум достигается на ребре многоугольника, лежащего в плоскости (x₁,x₂), когда линейная форма совпадает с одним из ограничений и сторона многоугольника в плоскости L(x₁,x₂) параллельна плоскости (x₁,x₂).

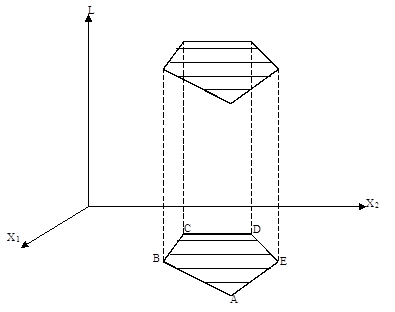
Рис. 2.7. Локальный (он же глобальный) экстремум в линейном программировании

Если функция цели нелинейная, то экстремум может достигаться в середине участка поверхности L(x₁,x₂) и экстремумов может быть несколько. Аналогичная ситуация может появиться при нелинейных ограничениях. Область допустимых значений тогда может быть многосвязной, и в каждой односвязной области достигается свой экстремум.

Таким образом, применительно к симплекс-методу геометрически задачу линейного программирования для случая двух переменных можно представить в следующем виде. Над допустимой областью значений (x₁,x₂) строится поверхность функции цели L(x₁,x₂). Так как функция цели линейная, то ее поверхность будет плоскостью в трехмерном пространстве. Расстояние любой точки поверхности L(x₁,x₂) до горизонтальной плоскости (x₁,x₂) равно значению целевой функции при соответствующих x₁, x₂. При симплекс-методе ищется вершина, наиболее или наименее удаленная от плоскости (x₁,x₂). Если взять три переменных, то необходимо провести четырехмерную плоскость. Область допустимых значений ограничена многогранником в четырехмерном пространстве. Очевидно, что экстремум в этом случае будет достигаться или в вершине, или на ребре, или на грани. Аналогичная ситуация имеет место и в случае любого числа переменных, только тогда будут многомерные многогранники и плоскости.

При нелинейности функции цели в случае двух переменных целевая поверхность может иметь несколько минимумов или максимумов и возникает так называемая многоэкстремальная задача, где требуется определить глобальный экстремум.

Обычно считается, что линейная форма зависит от всех переменных

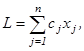
но в частных случаях некоторые из c_j равны нулю. На первом шаге выбирают m базисных переменных. Решение системы уравнений

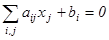
при нулевых значениях небазисных координат называется базисным решением. В качестве базисных переменных можно выбрать любые m переменных, для которых векторы а_i = ||a_ij|| линейно независимы, т.е. детерминант матрицы ||a_ij|| отличен от нуля. Однако на первом шаге их необходимо выбрать так, чтобы базисное решение, соответствующее началу координат косоугольной системы, принадлежало допустимой области (было бы одной из ее вершин). Вопрос о выборе начального базиса (базисного решения) требует специального рассмотрения, которое будет выполнено ниже.