Общая теория симплекс-метода на базе линейной алгебры

Рассмотрим задачу линейного программирования

(2.17)

a_i₁x₁ + a_i₂x₂ +... + a_inx_n = b_i, i = 1,..., m;

L = c₀ +c₁x₁ + c₂x₂+... +c_nx_n → min, 0 ≤ x_i.

Будем считать, что система уравнений (2.17) содержит r линейно независимых уравнений, где r ≤ m. Эти r переменных на первом шаге являются базисными переменными, т.е. определяют базис. Строго говоря, с практической точки зрения можно считать, что r = m, так как в противном случае равенства (2.17) или несовместны, или хотя бы одно из них представляет линейную комбинацию остальных и поэтому является лишним. Разрешив уравнения (2.17) относительно этих переменных, получим

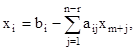i = 1, 2,..., r.

(2.18)

Без потери общности можно считать, что независимы первые r уравнений (2.17). Предположим, что свободные коэффициенты b_i неотрицательны. Каждое из этих уравнений можно рассматривать как проекцию векторного уравнения

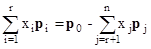
на единичные векторы, направленные по координатным осям (ортам) p ₁, p ₂,..., p _r, где

p ₁ = (1,0,...,0);

p ₂ = (0,1,0,...,0);

p _r = (0,0,...,1).

Векторы p ₁, p ₂,..., p _r образуют базис в m-мерном пространстве (рис. 2.8). При этом матрица разложений векторов p ₀, p ₁, p ₂,..., p _n в базисе p ₁, p ₂,..., p _r представляется в виде

(2.19)

В этой матрице первые r столбцов представляют собой орты системы координат. Столбец r+1 состоит из свободных членов ограничений. Последние n–r столбцов состоят из компонент проекций вектор-столбцов p _r+1,..., p _n на орты p ₁, p ₂,..., p _r. В целом матрица состоит из n + 1 вектор-столбцов с m компонентами каждый.

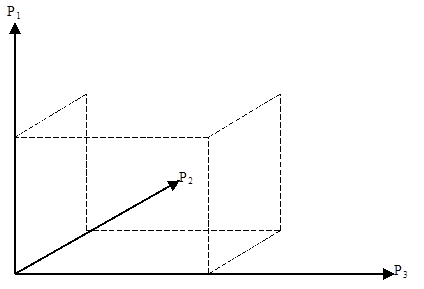
Рис. 2.8. Геометрическая интерпретация базисных переменных для трехмерного случая

Cимплекс-таблица теперь примет вид.

Таблица 2.5

		x_r+1	…	x_n
x₁	b₁	a_1,r+1	...	a_1n
x₂	b₂	a_2,r+1	...	a_2n
.		.
.		.
.		.
x_r	b_m c₀	a_r,r+1 c₁	... ...	a_rn c_n

Причем, соотношение для L запишется как

L = c₀ – 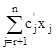, j = 1, 2,..., r.

После процедуры включения в базис небазисных переменных и исключения базисных, отвечающих ряду требований, получим группу векторов p ₁, p ₂,..., p _i1,..., p _r образующих новый базис. Их определитель, записанный в старой системе координат, отличен от нуля.

Следовательно, эти векторы независимы и могут быть выбраны за новый базис. Повторяя этот процесс до тех пор, пока все числа в последней строке симплекс-таблицы 2.5 станут неположительны, получим оптимальное решение. Еще раз напомним, что в практически важных случаях r = m.

Обсудим методы отыскания начальной вершины многоугольника.

Допустим, задача линейного программирования записана в виде

(2.20)

Ах = b;

Cx → min;

x ³ 0,

где b ³ 0; C = ||c₁, c₂,..., c_n||. Стартовый базис считается найденным, если ограничения, содержащиеся в задаче (2.20), записаны как

x_v = b_v – (a_v_,m+1x_m+1+... + a_v_nx_n), v = 1, 2,..., m,

где b_v ³ 0, так как, положив небазисные переменные x_m+k = 0 (k = 1, 2,..., n–m), получим значения x_v = b_v ³ 0, которые являются допустимыми и соответствуют одной из вершин.

Иногда сразу удается выделить первый базис. Однако в общем случае это непростая задача.

(2.21)

Для каждого ограничения вводим вспомогательную переменную z_i (i = 1,..., m). Тогда ограничения системы (2.20) будут выглядеть как

Ax + z = b; x ³ 0, z ³ 0.

Без нарушения общности считаем, что b неотрицательна, так как этого всегда можно достигнуть, поменяв соответствующие знаки в строках матрицы А. Поэтому допустимым базисным решением будет х = 0, z = b. Соответствующая симплекс-таблица на первом шаге запишется в виде

z = b – Ax,

т.е. за базис взят вектор z.

На первом шаге минимизируется функция цели ∑z_j при ограничениях (2.21). Непосредственно из этих ограничений следует, что если минимум функции ∑z_j является положительной величиной, то система (2.21) не имеет неотрицательных решений, для которых z₁,...,z_m =0, так как в противном случае min∑z_j = 0. Это означает, что исходная система (2.21) не имеет неотрицательных решений. Если min∑z_j = 0, т.е. z_j = 0 для всех j, то вектор z является базисным. Отправляясь от этого базиса, мы стремимся прийти к базису, не содержащему ни одной вспомогательной переменной:

x_v = b_v – (a_v,_m+1x_m+1 +... + a_v_nx_n + a_v₁z₁ +... + a_v_mz_m), v = 1, 2,..., m,

где b_v ³ 0. Полагая в системе (2.21) z_j = 0, придем к системе

x_v = b_v – (a_v_,m+1x_m+1 +... + a_v_nx_n), v = 1, 2,..., m,

которая равносильна исходной (2.20). Но здесь х₁, х₂,..., x_m – базисные переменные. Следовательно, задача нахождения базиса решена. Может получиться, что при переходе от базиса z₁, z₂,..., z_m к следующему эти переменные будут оставаться в следующем базисе. Тогда необходимо постепенно их перевести в небазисные.

Если среди неизвестных х₁, х₂,..., x_m имеется такая переменная, например х₁, которая входит только в одно уравнение, например в первое, причем коэффициент при этой переменной a₁₁ имеет тот же знак, что и свободный член b₁, тогда не имеет смысла вводить для первого уравнения искусственную переменную, так как х₁ сразу войдет в базис. Действительно, первое уравнение можно представить в виде

x₁ = b′₁ – (a′₁₂x₂ +... + a′_1nx_n),

где b′₁ = b₁/a₁₁ ³ 0. Если таких неизвестных несколько, то все их можно сразу включить в базис.

Пример. Дана система

x₁ – 2x₂ + x₃ = 2;

–x₁ – 4x₂ + x₄ = –8;

x₁ + x₂ + x₅ = 10;

–2x₁ + x₂ + x₆ = 2,

рассмотренная в примере ранее. Так как x₃, х₅, х₆ входят каждая только в одно ограничение и коэффициенты при них имеют тот же знак, что и соответствующие свободные члены, включаем их сразу в базис. Для оставшегося ограничения вводим искусственную переменную z₁. В итоге получаем:

x₃ = 2 – (x₁ – 2x₂);

x₅ = 10 – (x₁ + x₂);

(2.22)

x₆ = 2 – (-2x₁ + x₂);

z₁ = 8 – (x₁ + 4x₂ – x₄);

x₁ ³ 0; z₁ ³ 0.

С помощью симплекс-метода требуется минимизировать форму

L₁ = z₁ = 8 – (x₁ + 4x₂ – x₄)

при ограничениях (2.22). Составляем симплекс-таблицу на первом шаге.

Таблица 2.6

		x₁	x₂	x₄
x₃ x₅ x₆ z₁ L₁ L		–2	–2 –1	–1 –1 –1

Необходимо минимизировать L. Опорный элемент выбираем на пересечении строки x₃ и столбца x₁. После первого шага получаем базис (х₁, х₅, x₆, z₁). На втором шаге опорный элемент выбирается на пересечении строки z₁ и столбца x₄, поэтому искусственная переменная z₁ выводится из базиса. При этом L₁ = 0. Таким образом, базис найден и состоит из х₁, х₂, x₅, x₆: