Группа аффинных преобразований и её подгруппы. Предмет аффинной геометрии

1°. Понятие группы было рассмотрено в курсе алгебры. Пусть имеется некоторое непустое множество преобразований. Из определения группы следует, что 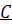является группой относительно композиций преобразований, то есть их последовательного выполнения, если выполняются следующие условия:

1.) Композиция любых двух преобразований из также принадлежит .

2.) Для композиции преобразований из справедлив ассоциативный закон.

3.) В содержится тождественные преобразования (играет роль единичного элемента).

4.) Преобразование, обратное любому преобразованию из , также принадлежит .

Известно, что второе условие выполняется для любых преобразований. Из выполнения первого и четвертого условий следует выполнение третьего условия: из

Следовательно, если мы хотим доказать, что является группой, то так достаточно проверить выполнение лишь первого и четвертого условий.

Теорема 1: множество аффинных преобразований пространства 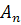является группой.

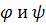□ 1) Пусть , докажем, что . Обозначим через ассоциированные с векторные преобразования. Пусть для произвольных точе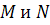к : . Так как – аффинные преобразования, что по определению (1) из §7

Так как 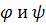– линейные преобразования, то и - линейное преобразование. Из (1) следует, что векторное преобразование ассоциировано с преобразованием . По определению (1) из §7 - аффинное преобразование.

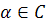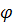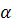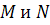
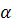4.) Пусть , покажем, что обратное ему преобразование . Обозначим через линейное преобразование, ассоциированное с . Пусть для произвольных точек , а так как - аффинное преобразование, то , откуда 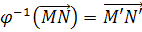. Следовательно, – линейное преобразование, ассоциированное с , и – аффинное преобразование. ■