Свойства степенных рядов. 1. Степенные ряды можно почленно складывать, причем если ряд (1), имеет радиус сходимости R1, а ряд (2) имеет радиус сходимости R2

1. Степенные ряды можно почленно складывать, причем если ряд 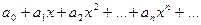(1), имеет радиус сходимости R₁, а ряд 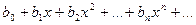(2) имеет радиус сходимости R₂, то ряд 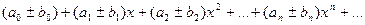, имеет радиус сходимости R, который не меньше наименьшего из чисел R₁ и R₂.

2.Степенные ряды можно умножать по правилу умножения многочленов, причем радиус сходимости ряда, получившегося в результате умножения снова не меньше наименьшего из чисел R₁ и R₂.

3.Сходящийся степенной ряд можно почленно дифференцировать внутри промежутка сходимости (-R_1; R₂) любое число раз.

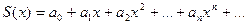
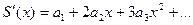
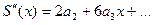
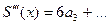
Область сходимости продифференцированных рядов есть также (-R_1; R₂).

4.Сходящийся степенной ряд можно почленно интегрировать в любом промежутке лежащем внутри области сходимости (-R_1; R₂) данного ряда.

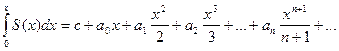
Область сходимости нового ряда есть интервал

(-R_1; R₂).