Сходимости ряда

Абсолютная и условная

Теорема: знакопеременный ряд U₁+U₂+U₃+…+U_n+… (1) сходится, если сходится ряд, составленный из абсолютных величин из абсолютных величин членов знакопеременного ряда.

Доказательства теоремы можно найти в каждом из учебников указанных в начале темы.

Определение1. Знакопеременный ряд (1) называется абсолютно сходящимся, если сходятся как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Определение2. Знакопеременный ряд называется условно сходящимся, если сходится сам ряд, а ряд, составленный из абсолютных величин его членов, расходится.

Рассмотрим примеры на абсолютную и условную сходимости.

Пример1. Исследовать на сходимость ряд

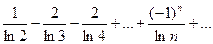
Решение: этот ряд на основании теоремы Лейбница сходится: абсолютная величина его членов убывает, его общий член 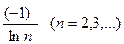имеет пределом 0, когда .

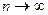Чтобы решить вопрос об абсолютной или условной сходимости этого ряда, составим ряд из абсолютных величин его членов

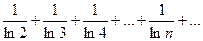
Этот ряд расходится, так как его члены больше соответствующих членов гармонического ряда.

Поэтому исследуемый ряд сходится условно.

Пример2. Исследуем на сходимость ряд:

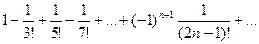
Исследуем по признаку Лейбница

а) Члены ряда монотонно убывают

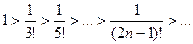
б) Находим предел U_n при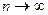

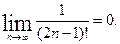
в силу признака Лейбница ряд сходится.

Исследуем как он сходится: абсолютно или условно.

Составим ряд из абсолютных величин его членов.

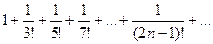
Исследуем полученный ряд по признаку Даламбера.

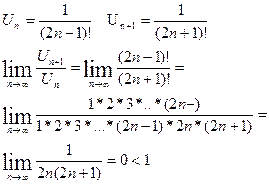
ряд сходится, следовательно, знакочередующийся ряд сходится абсолютно.

Вывод. Теория рядов имеет большое практическое применение в виду возможности при широких условиях представления данной функции в виде бесконечного ряда более простых функций.

В экономике бесконечные ряды и их суммы появляются в основном в теоретических исследованиях.

Тесты для самоконтроля знаний.

1.Ряд U₁+U₂+…+U_n+… называется сходящимся, если предел его частичной суммы равен:

а)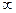; б)S; в)не существует.

2.Ряд U₁+U₂+…+U_n+… будет сходиться в силу необходимого признака если предел U_n при 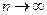равен: а)0; б) 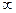; в) 1.

3.При исследовании ряда на сходимость с помощью признака сравнения рядов следует исходный ряд сравнить с:

а) гармоническим рядом или бесконечно убывающей геометрической прогрессией;

б) частной суммой ряда;

в) знакочередующимся рядом.

4.Знакочередующийся ряд исследовать на сходимость с помощью признака:

а) Даламбера; б) Коши; в) Лейбница.

5.Если ряд, составленный из абсолютных величин членов данного ряда сходится, то сам ряд:

а) расходится; б) абсолютно сходится; в) условно сходится.