N n n n n

X

A3

A2

A1

4.

2.

I

П

A · A

5 0

/1 2 3\ /3 6 9

Пример 3. Пусть Л = 3и A =(|. Тогда 3A= i

Произведением, млтрицы A = { а _ij} размера m × гг на матрицу B = { 6 _ij} размера п × к называют матрицу С = {c_ij} размера m × к, элементами которой являются всевозможные произведения строк матрицы A на столбцы матрицы B. Обозначение: С = A · B или С = AB. Это определение не является полным.

Пример 4. Пусть A= i |и B = - 1 0|. Тогда

1 · 1 - 2 · (- 1) + 3 · 2 1 · 1 - 2 · 0 + 3 · 3 9 10

AB 0 · 1 + 4 · (- 1) + 1 · 2 0 · 1 + 4 · 0 + 1 · 3 -2 3

Таким образом, элемент c_ij, стоящий на пересечении г-ой строки и j -ro столбца, равен произведению г-й строки матрицы A и j -ro столбца матрицы B^'. Поэтому умнож;ить A иа B можно только в том случае, когда длина строк матрицы A сов­падает с высотой столбцов матрицы B, т. е. "внутренние" размеры п в выраж;ениях m × п и п к должны оказаться равными. А размером произведения AB будет вы-раж;ение × к, равное произведению "внешних размеров" в выраж;ениях m × п я п × к.

Пример 5. Пусть B = \ -1 0 \ я A = 4. Тогда

11 10 23

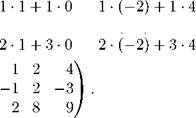1 · 3 + 1 · 1 BA =| - 1 · 1 + 0 - 1 · (- 2) + 0 · 4 - 1 · 3 + 0 · 1

23 + 3 1

^^Совсем аккуратно: элемент c_j вычисляется но формуле c_j = a ₁ b1j + a j2 b 2 j + · · · + a j„ b

August 31, 2013 Курбатов В.Г. 6

Уже эти примеры показывают, что A ■ В = В ■ A.

Отметим равенства: A + 0 = 0 + A = A, A-A = 0,A-0 = 0-A = 0,

A-Е = Е-A = A.

Здесь Е — единичная, а О — нулевая матрицы соответствующих размеров. Отметим тоясдество:

(AВ) = В'A'.

Пример 6. Пусть для изготовления одного стула требуется 4 единицы древесины и 1 единица материи, а для изготовления одного кресла требуется 6 единиц древесины и 5 единиц материи. Преднолоясим, что мы хотим изготовить х стульев и у кресел. Тогда расход материалов описывается следующим произведением матриц

древесина

материя

46 15

1.3 Определители второго порядка

Определителем матрицы A = all all размера 2x2 называют число a ₁₁ a ₂2 -a 12 a 215 обозначаемое символами

a 11 a 12 a 21 a 22

∆, detA, \A\,

Это правило удобно представлять себе в виде рис. 1.

Рис. 1: Диаграмма для вычисления определителя 2-го порядка.

August 31, 2013 Курбатов В.Г.

21
Пример 7. Ьсли A = 4' то

∆

21 34

2 · 4 - 1 · 3 = 5.

Замечание 1. Определители первого порядка обычно не рассматривают. Удобно счи-татв, что определителв матрицв:, состоящей из одного числа (т. е. матрицв: размера 1x1), равен этому числу.

1.4 Определители третьего порядка

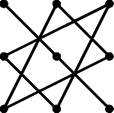
Определителем матрпцв! A размера 3x3 называют число, вычисляемое по пра­вилу, изображенному на рис 2. Обозначение преяснее.

Рис. 2: Правило треугольника вычисления определителя 3-го порядка.

Можно указать и аналитическую формулу:

a 11 a 12 a 13 ∆ = detA= \A\ = a 21 a 22 a 23 =

a 31 a 32 a 33 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - (a 13 a 22 a 31 + a 12 a 21 a 33 + a 11 a 23 a 32).

Пример 8,

\A\ =

	- 2
	- 5

= 1 • 0 • 2 + (- 2) • 6 • 4 + 3 • (- 1) • (- 5) - (3-0-4 + 1-6-(- 5) + (- 2)-(- 1)-2) = = 0 - 48 + 15 - 0 + 30 - 4 = - 7.

Задача 1. Вычислите определители матриц

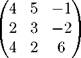
A =

	- 3
	- 2
		-

B =

Ответ: \A\ = 0, \B\ = - 4.

August 31, 2013 Курбатов В.Г. 8

1.5 Свойства определителей

в этом параграфе обсуясдаются свойства определителей третьего порядка. По­лезно уясе сейчас иметь в виду, что точно такие ясе свойства имеют место и для определителей любого порядка.

Свойство 1. При транспонировании матрицы ее определитель не меняется: \A'\ = \A\.

Свойство 2. Если поменять местами две строки {или два столбца), то определитель изменит знак на нротивонолож.ный, но но абсолютной величине не изменится.

Свойство 3. Определитель, имеющей две одинаковые строки (или два одинаковых столбца), равен нулю.

Свойство 4. Если строку (столбец) определителя умнож.ить на некоторое число, то определитель умиоукится на это число. Общий множ.итель из строки (столбца) МОЖ.НО выносить за знак определителя.

Свойство 5. Определитель, имеющий две пропорциопальпые строки (или столбца) равен нулю.

Свойство 6. Если определитель имеет нулевую строку (или столбец), то он равен нулю.

Свойство 7. Если определители ∆1 я ∆2 отличаются только k-ми строками (столб­цами), то их сумма ∆1 + ∆2 равна определителю ∆, k-ая строка (столбец) которого является суммой k-х строк (столбцов) определителей ∆1 и ∆2, а остальные строки (столбцы) — такие ж:е как в определителях ∆1 и ∆2. Например, если k = 2, то

a 11	a12 + a12	a 13		a 11	a 12	a 13		a 11	a 12	a 13
a 21	a22 + a 22	a 23	=	a21	a 22	a 23	+	a21	a 22	a 23
a 31	a 3 2 + a 3 2	a 33		a31	a 32	a 33		a31	a 2	a 33

Свойство 8. Определитель не изменится, если к какой-либо его строке (столбцу) прибавить другую строку (столбец), умнож:енную на число.

Обоснование:

a 11 a12 + a 11 a13

a21 a22 + a21 a23 a31 a32 + a31 a33

a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

a 11 a 11 a 13 a 21 a 21 a 23 a 31 a 31 a 33

Свойство 9. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

Например,

= 3 • 5 • 7 .

Свойство 10. Определитель произведения двух матриц A и B равен произведению

определителей этих матриц: \AB\ = \A\ ■ \B\.

August 31, 2013 Курбатов В.Г. 9

1.6 Символ суммирования

Для сокращенного обозначения суммы нескольких однотипных слагаемых ис­пользуют символ ^. Правила его использования аналогичны использованию опе­ратора цикла DO в программировании.

Выраясение Y1 k 2 читают так: "сумма по k от 1 до 3 выраясепий k ² ". Это выраясе- k =1 ние является сокращенной записью суммы 12 + 22 + 32.

Пример 9.

^А 1 = 1 1 1 1 ^ m 2 + 3 + 4 + 5,

_m=2

Y,i2 = 32 + 4² + ··· + n ²,

i =3

n

cij = aikbkj.

k =1

1.7 Миноры и алгебраические дополнения

Вычеркнем из определителя i -ю строку и j -й столбец. В результате получим опре­делитель меньшего порядка, который называют минором элемента a_ij и обозначают Mij. А величину

A_ij = (- 1) ^{i + j} M_i

называют алгебраическим дополнением элемента a_ij.

1 - 3 - 1

Пример 10. Если ∆ =

2 3 6, то
4 0 - 2

M = M =

1 - 3 4 0 A 23 =(- 1)2+3 · M 23 3 - 1 3 6 A 31 =(- 1)3+1 · M

= 0 + 12 = 12,

- 1 · 12 = - 12, = - 18 + 3 = - 15, ₃₁ = 1 · (- 15) = - 15.

Свойство 11 (теорема Лапласа). Сумма произведений элементов aij произвольной строки {плп столбца) определителя на алгебраические донолнення Aij этих элемен­тов равна определителю:

∆ = > aijAij, i = 1,2, 3,

^ —' j =1

j = 1,2,3.

∆= a_ijA_ij,

i =1

August 31, 2013 Курбатов В.Г.

Эти формулы называют правилами раскрытия (разлоснсения) определителя по строке (по столбцу).

Пример 11. Вычислим определитель, разлоясив его по первому столбцу:

			- 2 3
∆ =	- 1	06 - 5 2	=
0 6 - 5 2	- (-	1) ·	- 2 3 - 5 2	+ 4 ·	- 2 3 0 6

= 1 ·

= 1 · (0 + 30) + 1 · (- 4 + 15) + 4 · (- 12 - 0) = = 30 + 11 - 48 = - 7.

1.8 Определители n -го порядка

в качестве определения определителя n -го порядка примем формулы из свой­ства 11

∆ = У aijAij, L —/ j =1

∆ =2. i aijAij,

i = 1, 2 ,..., n, j = 1, 2 ,..., n.

Эти формулы позволяют понизить порядок определителя, т. е. свести вычисление определителя n -го порядка к вычислению определителей (n - 1)-го порядка.

Пример 12. Вычислим определитель четвертого порядка, раскрывая его по первому столбцу:

	- 1

21 01	= - 1 ·

2 1 1

	- 0 ·

230 101 112

	- 2 1	- 3 ·

= - 1 · (2 + 1 - 2 + 4)+

2 3 0 2 - 2 1 1 0 1

+6 · (- 8 - 3 - 2 - 12) - 3 · (- 4 + 3 - 6) =

= 5 150 + 21 = 134.

1.9 Метод элементарных преобразований вычисления определителя

Укажем еще один способ вычисления определителей n -го порядка. Напомним (§ 1.5) некоторые свойства определителей:

2) если переставить две строки (или два столбца), то определитель поменяет знак;

August 31, 2013 Курбатов В.Г.

4) если строку (столбец) умноясить на число, то и определитель умножится на это число; общий множитель из строки (столбца) мож;но выносить за знак опреде­лителя;

8) если к одной строке (или столбцу) прибавить другую, умноженную на число, то определитель пе изменится.

Перечисленные в этих свойствах преобразования называют элементарными. С по­мощью элементарных преобразований определитель приводят к треугольному виду, после чего он вычисляется с помощью свойства 9: определитель треугольной матри­цы равен произведению элементов, стоящих на главной диагонали.

Пример 13. Вычислим определитель из предыдущего примера методом элементар­ных преобразований. ЭТАП 1: Сформируем сначала нули в первом столбце под диаго­налью. Для этого прибавим к третьей строке первую, умнож;епную па 6, а к четвертой — первую, умнож;епную па 3. В результате получим

	- 1

		- 2 1
		18 1
		10 2

ЭТАП 2: Сформируем нули во втором столбце под диагональю. Сначала поме­няем местами 2-й и 4-й столбцы, после чего к третьей строке прибавим вторую, умпож;еппую на - 1, а к четвертой — вторую, умнож;еппую на - 2:

12 02 0 13 05

10 3 2

0 1 - 2 2

0 1 18 13

0 2 10 5

10 3 2

0 1 - 2 2

0 0 20 11

0 0 14 1

ЭТАП 3: Сформируем нули в третьем столбце под диагональю. К четвертой стро-

14 7

ке прибавим третью, умпож;еппую па - — = - 10-

- 103 2 0 1 - 2 2 0 0 20 11 0 0 0 - 67 / 10 (- 1) · 1 · 20 · (- 67 / 10) = - 134.

10 3 2

0 1 - 2 2

0 0 20 11

0 0 14 1

В конце мы воспользовались правилом вычисления определителя треугольной матрицы.

1.10 Ранг матрицы

Рассмотрим матрицу A размера m×n. Возьмем число k, меньшее или равное как m, так и n. Выделим в матрице любые k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют определитель k-то порядка. Его

August 31, 2013 Курбатов В.Г.

называют минором матрицы A порядка к. Очевидно, что мииоров порядка к, вообще говоря, много.

Рангом матрицы A называют наибольший порядок отличного от нуля минора этой матрицы. Иными словами, число г называют рангом ненулевой матрицы A, если: 1) у матрицы A есть ненулевой минор порядка г; 2) всякий минор порядка г + 1 и выше равен нулю. Ранг матрицы A обозначают символом rang A.

Ранг матрицы, состоящей из одних нулей, равен нулю.

Всякий ненулевой минор матрицы, порядок которого равен рангу, называют ба­зисным минором. Строки и столбцы, на пересечении которых находится базисный минор, называют базисными строками и базисными столбцами. Замечание 2. Из определения ранга непосредственно следует, что если определитель квадратной матрицы A отличен от нуля, то rang A = п. Пример 14. Рассмотрим матрицу

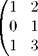3 4

- 1 2

2 6

Нетрудно проверить, что все ее миноры 3-го порядка равны пулю:

2 1 3

		1 2 4
	=	0 1 2	=
		1 3 6

= 0.

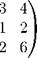
= 1 = 0.

А минор 2-го порядка

Поэтому rang A = 2. Напомним, что

1 2

0 1

1 3

1.11 Метод элементарных преобразований вычисления ранга

в § 1.9 уж;е отмечалось, что элементарные преобразования сохраняют свойство определителя быть отличным от пуля. Поэтому элементарные преобразования не меняют такж;е и ранг матрицы. Таким образом, метод элементарных преобразований моясет быть применен и к нахождению ранга. Это делается с помощью приводимой пиж;е теоремы.

Матрицу называют ступенчатой, если каждая ее строка начинается со строго большего числа нулей, чем предыдущая. Ненулевые элементы а^- ступенчатой мат­рицы A, левее которых стоят только нули (а также места, на которых они находятся), называют началами ступенек. Пример 15. Пример ступенчатой матрицы:

/8 10 3 1 5 \

0 6 4 - 20 - 3

0 0 0 0 4 - 2

0 0 0 0 0 0

August 31, 2013 Курбатов В.Г. 13

Теорема 1. Ранг ступенчатой матрицы равен числу ненулевых строк в ней.

Преобразовать матрицу к ступенчатому виду можно с помощью элементарных преобразовапий.

Задача 2. Найти ранг матрицы

A = Решение. Приведем матрицу к ступенчатому виду:

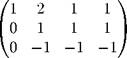
Получеппая матрица является ступенчатой: начала ступенек образовались на местах
элементов a ₁₁ и a 22- В силу теоремы 1 получаем, что rang A = 2. П

1.12 Обратная матрица и ее нахож:дение методом присоединенной матрицы

Пусть A — квадратная матрица, а E — единичная матрица того ж;е размера. Матрицу B называют обратной к матрице A, если AB = EжBA = E. Обратную матрицу обозначают символом A- ¹. Таким образом, · о определе · ю имеем

AA^{- 1} = A^{- 1} A = E.

1 2
Пример 16. Для A = 1 1 обратной является

1 / 3 1 / 3 1 2\ /1 / 3 - 2 / 3

A- 1=/1 / 3 - 2 / 3

Действительно,

1 1 1 / 3 1 / 3

1 · (1 / 3)+ 2 · (1 / 3) 1 · (- 2 / 3) + 2 · (1 / 3) 1 0

1 · (1 / 3) + 1 · (1 / 3) - 1 · (- 2 / 3) + 1 · (1/3) 0 1

Нетрудно такясе проверить, что и A-1 · A = E.

Теорема 2. Квадратная матрица A имеет обратную тогда и только тогда, когда ее определитель |A| отличен от пуля.

Доказательство. Если A имеет обратную, то E = A A-1, откуда по свойству 10 определителей имеем 1 = j E! = |A · A^{- 1} | = \А\ \А~1\, от · уда видно, что |A| = 0.

В качестве доказатель || в обратную || · | у | ишем алгоритм построения об­
ратной матрицы для случая, когда |A| = 0. П

August 31, 2013 Курбатов В.Г. 14

Алгоритм построения обратной матрицы.

1. Вычисляем \A\. Если \A\ = 0, то ио доказанному A-1 не существует, и вычис­ления на этом заканчиваются. Если \A\ = 0, то переходим к этану 2.

2. Выписываем трапсиопированпую матрицу A.

3. Составляем матрицу A ˆ, состоящую из алгебраических дополнений элементов матрицы A. Матрицу A называют присоединенной к матрице A.

4. Выписываем ответ по формуле A- ¹ = щA.

5. Делаем проверку: проверяем равенства A ■ A^-1 = E я A-1 ■ A = E.

Пример 17. Найдем обратную к матрице

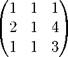
A

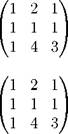
Решение. 1. Вычисляем \A\. Имеем \A\ = - 2. 2. Выписываем транспонированную матрицу:

A'

A' 3. Вычисляем ирисоединенную матрицу:

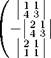
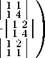
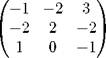
I 1 3 1 1 I 1 3 I I11 11

A =

Сформулируем правило расстановки знаков в присоединенной матрице. Элемен­ты, стоящие на главной диагонали, берутся со знаком "плюс", а остальные знаки расставляются в шахматном порядке. 4. Выписываем ответ:

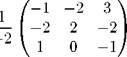
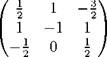
A-1 =

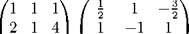
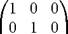
5. Проверяем:

AA-1 =

1 1 3 - ¹ ₂ 0 ¹ ₂ 0 0 1

Глава 2

Системы линейных уравнений

2.1 Основные понятия

Система из m линейных уравнений с n неизвестными имеет вид

a11x1 + a 12 x 2 + ... + a1nxn = b 1,

a21x1 + a 22 x 2 + ... + a2nxn = b 2,

(2.1)

a_{m 1} x ₁ + a_{m 2} x ₂ + ... + a_mnx_n = b_m.

Здесь через x 1, x 2,..., x_n обозначены неизвестные числа. Величины a_ij и bi пред­полагаются известными; при этом a_ij называют коэффициент,ами, abi — свободными членами или правыми частями.

В случае, когда m = n, систему называют квадратной, а когда m = n, — прямо­угольной.

Реиаением системы (2.1) называют такую совокупность n чисел α 1, α 2, ..., α_n, которая ири подстановке их в систему вместо x 1, x 2, ..., x_n превращает все уравнения в тождества.

Пример 18. Непосредственной подстановкой проверяется, что решением системы

x 1 + x2 = 3,

x ₁ + 2 x 2 = 5

являются числа x ₁ = 1 и x 2 = 2.

Если bi = 0 при всех i = 1, 2 ,..., m, то систему называют однородной. Если хотя бы один bi отличен от нуля, то систему называют неоднородной. Однородная система всегда имеет нулевое решение.

'a _{1 1} x1 + a 12 x 2 + ... + a1nxn = 0,

a 21 x 1 + a _{2 2} x 2 + ... + a2nx_n = 0, an1x1 + a_n2x2 + ... + a_nnx_n = 0.

Если система имеет хотя бы одно решение, то ее называют совместной. Если же у системы нет решений, то — несовместной.

August 31, 2013 Курбатов В.Г.

Пример 19. Система

x 1 + x 2 = 3 ,

x ₁ + x 2 = 5

несовместна, так как x1 + x2 не может одновременно равняться 3 и 5.

Если система имеет единственное решение, то ее называют определенной. Если у системы более одного решения, то — неопределенной. Нетрудно убедиться, что система из примера 18 имеет единственное решение, т. е. является определенной.

Пример 20. Система

x ₁ + x2 = 3,

2 x 1 + 2 x 2 = 6

является неонределенной. Прямой подстановкой моясно убедиться, что ее решениями являются (1,2), (2,1), (3,0), ....

Матрицу

' a11 a12... a1n \

a 21 a ₂₂... a 2 _n A =

am 1 am 2 ... a_mn

называют матрицей (коэффициентов) системы. А

a 11 a 21

D =

a 12 a 22

am 1 am 2

a 1 n a 2 n

b
b 2
bm

— расширенной матрицей системы.

Пример 21. Пусть для изготовления одного стула требуется 4 единицы древесины и 1 единица материи, а для изготовления одного кресла требуется 6 единиц древесины и 5 единиц материи. Па складе имеется 106 единиц древесины и 51 единица мате­рии. Какое количество x стульев и y кресел следует изготовить, чтобы полностью израсходовать материалы? Эта задача сводится к решению системы

4 x + 6 y =106, x + 5y = 51.

2.2 Метод Крамера

Рассмотрим квадратную систему из n уравнений с n неизвестными

' a 11 x 1 + a 12 x 2 + ... + a1nxn = b1, a 21 x 1 + a _{2 2} x 2 + ... + a2nxn = b 2,

(2.2)

, an1x1 + an2x2 + ... + a_nnxn = bn.

August 31, 2013 Курбатов В.Г.

Теорема 3. Для того чтобы квадратная система была определенной, т. е. имела единственное ретпенне, необходимо и достаточно, чтобы ∆ = \А\ у/^ 0. Если ∆ = |A| = 0, то ее едннственное ретпенне моукно вычислить но формул|

(2.3)

xj= ∆

j = 1,2,...,n,

где ∆j — определитель, получаемый из ∆ заменой j-го столбца на столбец свободных членов.

Задача 3. Решить методом Крамера систему

2x + 3y = 9, 3 x - y = 8.

Решение. Для рассматриваемой системы

∆i =33

∆2 ∆

∆i

	∆	=	2 3 3 - 1	=	- 11 ,
	3 - 1	=	- 33,	∆2		2 9 3 8

1.

3, y

Отсюда x

∆ - 11 ∆ - 11

Задача 4. Решить систему методом Крамера

= 11.

x + y + z = 2,

2x + y + 4z = 5,

x + y + 3z = 6.

∆

= 2 ,

6 ,

3, z

3, y

Решение. Имеем

∆ =

∆2 =

∆

Отсюда x

∆2

∆

∆з

∆

∆i =

∆

= 6 ,

Задача 5. При каких значениях λ система уравнений

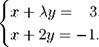
не является онределеннои.^

August 31, 2013 Курбатов В.Г.

Решение. В силу теоремы 3 система ие является оиределеииой, если \A\ = 0. Вы­числяем:

2 - λ.

\A\

1 λ

1 2

Из уравнения 2 — λ = 0, находим λ = 2. Значит, при λ = 2 система не является
определенной. П

2.3 Матричная запись

системы линейных уравнений

Запишем неизвестные и свободные члены в виде столбцов (матриц, размера n х 1 и m X 1, соответственно):

b2 bm

a 1 n a 2 n

x1 x2 xn

a 11 a 12 a 21 a 22

A

B

X

n

am1 am2...

Теорема 4. Система (2.1) эквивалентна равенству

A-X = B,

называемому матричной формой записи системы линейных уравнений. Доказательство. Вычисляем:

AX

a 11 a 12 a 21 a 22

a 1 n a 2 n

x ₁ x ₂

xn

am1 am2... a 1 1x 1 + a 12 x 2 + ... + a 1 nxn \ b 1 b 2

n

bm

a21x ₁ + a 22 x 2 + ... + a2nx_n a_{m 1} x1 + a_m2x2 + ... + a_mnx_n

Таким образом, приходим к равенству

B.

a ₁₁ x ₁ + a ₁₂ x ₂ + ... + a _{1 n} x_n a ₂₁ x ₁ + a ₂₂ x ₂ + ... + a _{2 n} x_n

b ₁ b ₂

am1x ₁ + a_m2x2 + ... + a_mnx_n b_m

В силу определения равенства матриц это равенство равносильно совпадению соот­
ветствующих элементов, что и представляет собой систему (2.1). П

August 31, 2013 Курбатов В.Г.

2.4 Метод обратной матрицы

Рассмотрим квадратную систему из n уравнений с n неизвестными

' a _{1 1} x ₁ + a 12 x 2 + ... + a1nxn = b 1,

a 21 x 1 + a _{2 2} x 2 + ... + a2nx_n = b 2,

(2.4)

an1x1 + a_n 2 x 2 + ... + a_nnxn = bn.

В соответствии с § 2.3, запишем систему в виде A- X = B.

Теорема 5. Пусть матрица A имеет обратную. Тогда решение уравнения A- X = B МОЖ.НО находить по формуле

X = A^{- 1} B.

Вычисление решения но этой формуле называют методом обратной матрицей.

Доказательство. Умножим обе части равенства

A- X = B на A- ¹. Получим A^-1 ■ A- X = A^-1 ■ B, или (поскольку A^-1 ■ A = E) E ■ X = A-1B или (поскольку E ■ X = X)

X = A^{- 1} B.

Пример 22. Рассмотрим систему

x + y + z =2,

2 x + y + 4 z = 5,

x + y +3 z = 6

или в матричной заниси

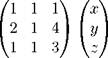
Из примера 17 известно, что

A^{- 1} =

Поэтому

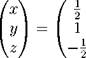
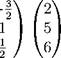
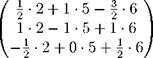
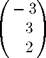
Иными словами, x = —3, y = 3, z = 2.

August 31, 2013 Курбатов В.Г. 20

2.5 Матричные уравнения

Прием, описанный в § 2.4, позволяет решать и более слоясные матричные урав­нения.

Задача 6. Решить матричное уравнение XA = B, где

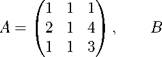
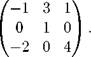
Решение. Умножая уравнение XA = B справа на A^- ^, получаем формулу XAA ^ BA-^ или X = BA^-^, по которой можно находить решение. Вычисляем:

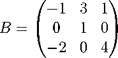
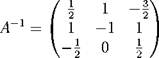
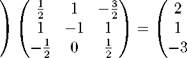
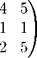
1 3 1 X = BA-^ = I 0 10 2 0 4

Задача 7. По какой формуле надо решать матричное уравнение AXB = F? Решение. Умножим уравнение слева на A^-^ и справа на B-^. Получим

A^{- 1} AXBB^{- 1} = A^{- 1} FB^{- 1},

EXE = A^{- 1} FB^{- 1},

X = A^{- 1} FB^{- 1}.

2.6 Метод Гаусса

Рассмотрим произвольную систему

a ₁₁ x ₁ + a ₁₂ x ₂ + ... + a _{1 n} x_n = b ₁, a ₂₁ x ₁ + a ₂₂ x ₂ + ... + a _{2 n} x_n = b ₂,

.........................................................

a_{m 1} x ₁ + a_{m 2} x ₂ + ... + a_mnx_n = b_m.

(2.5)

На этот раз не будем предполагать, что число уравнений m обязательно совпадает с числом неизвестных n.

Две системы линейных уравнений называют эквивалентными, если они имеют одно и то ж;е множество решений.

Элементарными преобразованиями системы линейных уравнений называют:

August 31, 2013 Курбатов В.Г.

1) перестановку двух уравнений местами;

2) умноясение уравнения на ненулевое число или сокращение на общий мнояси-

тель;

3) прибавление к одному уравнению другого, умноженного на некоторое число;

4) отбрасывание нулевых-*-) уравнений.

Ясно, что элементарные преобразования переводят систему в эквивалентную.

Элементарные преобразования системы аналогичны элементарным преобразова­ниям матриц,, поэтому для сокращения записи их обычно выполняют не с системой уравнений, а с ее расширенной матрицей

D =

a 21 a 22

a 1 n a 2 n

b 2 b_m

Напомним, что матрицу называют ступенчатой, если каждая ее строка начина­ется со строго большего числа нулей, чем предыдущая. Первый ненулевой элемент в строке ступенчатой матрицы A называют началом ступеньки. Будем различать ступеньки короткие и длинные.

Пример 23. Ступенчатой является матритщ

/8 10 3 1 5 \

0 6 4 - 20 - 3

0 0 0 0 4 - 2

0 0 0 0 0 0

Метод Гаусса заключается в преобразовании расширенной матрицы D (или, что эквивалентно, системы уравнений) с помощью элементарных преобразований сна­чала к ступенчатому виду (эту часть метода Гаусса называют прямым ходом), а затем по возмож;ности — к диагональному виду (эту часть метода Гаусса называ­ют обратным ходом). Возникающая в результате преобразований система уравнений легко решается. В промежутке меж;ду прямым и обратным ходом обсуж;дают вопрос о существовании и единственности решения. Уточним некоторые детали.

Меж;ду прямым и обратным ходом применяют два правила.

Правило 1. Если в последней строке расширенной матрицы, получившейся по­сле окончания прямого хода, до черты есть ненулевые числа, система совместна; если же в последней (ненулевой) строке до черты нет ненулевых чисел, то система несовместна.

Действительно, если последняя ненулевая строка имеет вид

(0 0 ... 0 I b),

^^Нулевым называют уравнение, в котором все коэффициенты, а также свободный члены равны нулю: 0 · x 1 + 0 · x 2 + ... + 0 · x „ = 0.

August 31, 2013 Курбатов В.Г.

где b_r = 0, то решений нет (система несовместна), поскольку этой строке соответ­ствует уравнение

0 x 1 + 0 x 2 + • • • + 0 x_n = b_r,

удовлетворить которому невозможно. Если же последняя ненулевая строка имеет вид

(0 0 ... ark ar _k +1 ... I b_r),

где a_rk = 0, то, как мы увидим, система совместна.

Если система оказалась совместной, то следует применить второе правило:^^ Правило 2. Если в расширенной матрице, получившейся после окоичапия пря­мого хода, все ступеньки короткие, то система является онределенной; если ж;е есть хотя бы одна длинная ступенька, то система является пеопределенпой.

Если система оказалась совместной, переходят к обратному ходу, используя эле­ментарные преобразования, делают нули над началами ступенек, а числа, стоящие на началах ступенек, по возмож;ности превращают в +1. В результате возникает си­стема, которая решается тривиальным образом.

Задача 8. Решить систему

x 1 + 2 x 2 + 3 x 3 + 4 x	4 = 5,
x 2 + 2 x 3 + 3 x 4 = 1,
x 1 + 3 x 3 + 4 x 4 = 2,
x 1 + x 2 + 5 x 3 + 6 x 4 = 1.
/12 3 4	5\
D =	0 12 3 10 3 4	1 2
1 156
м С выписывания расши];
1 234
D =	0 12 3 10 3 4	1 2
	1 156

После этого начинаем прямой ход. Его цель — сделать расширенную матрицу ступенчатой.

В качестве первого этапа прямого хода приводим к ступенчатому виду 1-ый стол­бец, а точнее — столбец, соответствующий началу первой ступеньки.

Для этого первые две строки переписываем без изменений (поскольку они удовле­творяют определению ступенчатой матрицы), к 3-ей строке прибавляем 1-ую, умно­женную на - 1 (иными словами, из 3-ей строки вычитаем 1-ую), и к 4-ой строке прибавляем 1-ую, умпож;еппую на - 1:

1 234
0 123
10 3 4		г-^		- 2 0 0	- 3
1 156				- 1 2 2	- 4

^^Его объяснению посвящен § 2.

August 31, 2013 Курбатов В.Г.

В качестве второго этапа прямого хода приводим к ступепчатому виду 2-ой стол­бец. Для этого первые две строки переписываем без измеиепий, к 3-ей строке при­бавляем 2-ую, умпоясенную на 2, а к 4-ой строке прибавляем 2-ую, умпоженпую на 1:

1 2 34
0 1 23
0 - 200	- 3		0 0 4 6	- 1
0 - 1 2 2	-4			- 3

В качестве третьего этапа прямого хода приводим к ступепчатому виду 3-ий столбец. Для этого первые три строки переписываем без изменений, а к 4-ой строке прибавляем 3-ую, умноясенную на - 1:

123 4			123 4
012 3			012 3
0 0 4 6	- 1	∼	0 0 4 6	- 1
004 5	- 3		0 0 0 - 1	- 2

Поскольку получилась ступенчатая матрица, прямой ход метода Гаусса закончен.

После окончания прямого хода применяем два правила, см. с. 21 п 22. Вывод 1: поскольку в последней строке до черты есть ненулевые числа, система является сов­местной. Вывод 2: поскольку все ступеньки являются короткими, система является определенной.

Переходим к обратному ходу, см. с. 22. Его цель — сформировать пули пад нача­лами ступенек. Поскольку в нашем случае все ступеньки короткие, это означает, что надо сформировать до черты диагопальпую (а еще лучше — единичную) матрицу.

В качестве первого этапа обратного хода приводим к единичному виду 4-ый стол­бец. Для этого последнюю строку умножаем на - 1, 4-ую строку умнож;аем на - 6 и прибавляем к 3-ей, 4-ую строку умнож;аем на - 3 и прибавляем к 2-ой, 4-ую строку умнож;аем на - 4 и прибавляем к 1-ой:^)

								- 3
								- 5
0 0 4		- 1	∼	0 0 4 6	- 1	∼	0 0 4 0	- 13
	- 1	-2

Па втором этапе обратного хода приводим к единичному виду 3-ий столбец. Для этого 4-ую строку оставляем без изменений, 3-ю строку умнож;аем на 1 / 4, 3-ю строку умнож;аем на - 2 и прибавляем к 2-ой, а 3-ю строку умножаем на - 3 и прибавляем к 1-ой:

	- 3
	- 5
	- 13

	- 3			27 / 4
	- 5			3 / 2
0 0 10	- 13 / 4		0 0 10	- 13 / 4

^^Термины "прямой ход" и "обратный ход" объясняются следующим обстоятельством. При пря­мом ходе движение идет сверху вниз и слева направо: верхние строки прибавляют к нижним, и на каждом шаге столбец, в котором формируют пули, передвигается вправо. При обратном ходе движение происходит в обратную сторону.

August 31, 2013 Курбатов В.Г.

На третьем этапе обратного хода приводим к единичному виду 2-ой столбец. Для этого 2-ую, 3-ю и 4-ую строки оставляем без изменения, а 2-ую строку умножаем на - 2 и прибавляем к 1-ой:

	27 / 4			15 / 4
	3 / 2			3 / 2
0 0 10	- 13 / 4		0 0 10	- 13 / 4

До черты образовалась единичная матрица. Поэтому обратный ход метода Гаус­са закончен.

x 1 x 2 x 3 x 4

Возвращаясь от полученной расширенной матрицы к системе уравнений, получа­ем

15 / 4,

3 / 2,

- 13 / 4,

2,

что фактически является ответом.

Правило. Если до черты получилась единичная матрица, то после черты нахо­дится решение.

2.7 Несовместная система

Задача 9. Решить систему

x 1 + x 2 + x 3	= 1,
x 1 + x 2 + 2 x 3	= 1,
x 1 + x 2 + 3 x 3	= 2.

Решение. Выполним элементарные преобразования прямого хода:

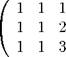
Поскольку ступенчатая матрица получена, применяем два правила, см. с. 21 и 22.
Вывод 1: поскольку в последней строке до черты стоят только нули (а после черты
есть ненулевой элемент), система несовместна, т. е. не имеет решений. П

Вновь рассмотрим систему обш,его вида (2.5). Обозначим через A матрицу систе­мы (2.5), а через D — расширенную матрицу.

Теорема 6 (Теорема Крбнекера-Капёлли). Если

ran gD > rang A, то система (2.5) несовместна, т. е. не имеет решений. Если же ran gD = rang A, то система (2.5) совместна, т. е. имеет решения.

August 31, 2013 Курбатов В.Г. 25

Пример 24. Вернемся к системе уравнений, рассмотренной в задаче 9. После преоб­разований мы получили расширенную матрицу

Видно, что rang D > rang A (см. теорему 1). Поэтому система несовместна.

Доказательство. Вернемся к ситуации, возникающей после окончания прямого хода метода Гаусса.

Если последняя ненулевая строка (имеющая для определенности номер r) матри­цы D имеет вид

(0 0 ... 0 I b_r),

где b_r = 0, то решений нет (система несовместна). По в этом случае но теореме 1 rang D = r, а rang A = r — 1. Таким образом, rang D > rang A.

Если же последняя ненулевая строка (имеющая для определеппости номер r) матрицы D имеет вид

(0 0 ... a_rk a_{r k} +1 ... I b_r ) ,

где a_rk = 0, то, как мы увидим ниясе, решения есть (система совместна). Но в этом случае но теореме 1 rang D = r и rang A = r. Таким образом, rang D = rang A. П

2.8 Неопределенная система

Обсудим подробнее второй возмоясный случай, возникший после окончания пря­мого хода метода Гаусса: имеются длинные ступеньки. Покаясем, что в этом случае система совместна, т. е. имеет решения но является неопределенной. Мы сделаем это путем предъявления алгоритма нахождения решения.

Неизвестные, соответствующие столбцам, на которых располож;ены начала сту­пенек, называют базисными, а остальные неизвестные — свободными. Вернемся от расширенной матрицы к системе уравнений. Свободные неизвестные обозначим про­извольными буквами, например, C ₁, C ₂,...; это означает, что им позволяется при­нимать любые значения. Получится система относительно базисных неизвестных. Решая ее, получаем выраж;ения базисных неизвестных через C ₁, C ₂,....

Решение, в котором все C ₁, C ₂,...равны нулю, называют базисным.

Таким образом, в этом случае решений оказывается бесконечно много — при каж­дом новом выборе C 1, C 2, ... получается новое решение. Еще раз подчеркнем, что свободные неизвестные, а с ними и бесконечное множество решений появляются толь­ко в том случае, когда есть "длинные" ступеньки.

Задача 10. Решить систему

x +2 y + z =	1,
x + 2 y + 3 z =	1,
x +2 y- z =	1.

August 31, 2013 Курбатов В.Г.

Решение. Преобразуем расширенную матрицу системы в соответствии с методом Гаусса. Прямой ход:

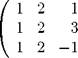
	- 2

Обратный ход:

121 001

120 001

Поскольку в последней ненулевой строке есть ненулевое число до черты, система совместна. По поскольку есть "длинная" ступенька, решений бесконечно много. В соответствии с видом полученной ступенчатой матрицы в качестве базисных неиз­вестных возьмем x и z, а в качестве свободной — y.

Обозначая свободную неизвестную y через C и перенося ее вправо, приходим к системе уравнений

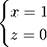
x + 2 y

= 1, z = 0,

2 C,

относительно x и z.

По сути это уже готовый ответ: x = 1 — 2C, y = C, z = 0, где C — произвольное
число. Подчеркнем, что при различных C будут получаться разные решения. Так,
например, при C = 0 имеем x = 1, y = 1, z = 0. При C = 1 получаем x = —1, y = 1,
z = 0. А при C = 3 имеем x = —5, y = 3, z = 0. П

Задача 11. Решить систему

x +2 y + z =	1,
x +2 y + z =	1,
2 x + 4 y + 2 z =	2.

Решение. У этой системы матрицы A и D имеют одинаковые 1-ю и 2-ю строки, а 3-я строка пронорциональна 1-й. Поэтому после преобразований по методу Гаусса мы приходим к расширенной матрице, содерж;аш,ей единственную ненулевую строку

или, что эквивалентно, к единственному уравнению

x

2 y

1.

Очевидно, оно имеет бесконечно много решений. Чтобы их найти, в соответствии
с нашим правилом в качестве свободных неизвестных примем y и z, а в качестве
базисной — x. Положим y = C1, z = C2 я перенесем их в правую часть уравнения.
В результате получим x = 1 — 2C1 — C2. Таким образом, все решения задаются
формулами x = 1 — 2C1 — C2, y = C1, z = C2, где C 1 и C ₂ — произвольные числа.
Отметим базисное решение: x = 1, y = 0, z = 0. П

August 31, 2013 Курбатов В.Г.

2.9 Система линейных однородных уравнений

Система линейных однородных уравнений

'a _{1 1} x ₁ + a 12 x 2 + ... + a1nxn = 0,

a 21 x 1 + a _{2 2} x 2 + ... + a2nx_n = 0,

(2.6)

всегда имеет нулевое решение x 1 = 0, x 2 = 0,..., x_n = 0, называемое тривиальным.

Теорема 7. Однородная система имеет ненулевое решение тогда и толвко тогда, когда ранг ее матрнтщ строго менвгие сила неизвестных: rang A < n.

Если в системе уравнения линейно независимы, то условие rang A < n означает, что число уравнений строго меньше числа неизвестных.

Теорема 8. Если x = (x1,x2,...,x_n) — решение однородной системы, то αx = (αx1,αx2,..., αx_n) — такуке решение.

Если x = (x 1, x 2 ,..., x_n) и y = (y ₁, y 2 ,..., y_n) — рсшсния однородной системы, то их сумма x + y = (x1 + y1, x2 + y2,..., x_n + y_n) ~ такуке решение.

Линейная комбинация решений — снова решение.

Набор решений e 1, e 2,..., ek однородной системы называют фундаментальной системой решений, если 1) они линейно независимы и 2) любое решение является их линейной комбинацией. Поэтому общее реиаение системы (2.6) имеет вид

C ₁ e ₁ + C ₂ e ₂

C_ke_k.

Теорема 9. Всякая фундаменталвная систем