1) Линейность: если 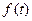 и
и 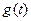 - оригиналы, а их изображения
- оригиналы, а их изображения 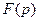 и
и 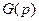 соответственно, то
соответственно, то 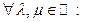 изображением функции
изображением функции 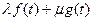 будет
будет 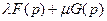 .
.
2) Подобие: пусть 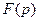 изображение
изображение 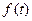 , тогда для любого
, тогда для любого 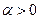 функция
функция 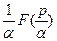 будет изображением
будет изображением 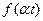 .
.
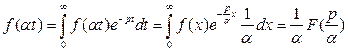
■
3) Дифференцирование оригинала:
Пусть 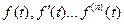 - оригиналы и
- оригиналы и 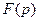 изображение
изображение 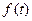 , тогда
, тогда
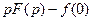 изображение
изображение 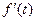 , где
, где 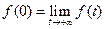 ,
,
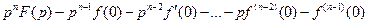 изображение
изображение 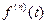 .
.
4) Дифференцирование изображения:
Пусть 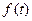 оригинал, а
оригинал, а 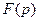 его изображение, тогда
его изображение, тогда 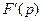 изображение
изображение 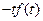 ,
, 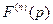 изображение
изображение 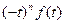 .
.
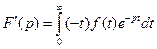 , а это изображение
, а это изображение 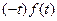
■
5) Интегрирование оригинала:
Пусть 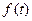 оригинал, а
оригинал, а 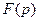 его изображение, тогда
его изображение, тогда 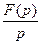 изображение функции
изображение функции 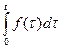 .
.
6) Пусть 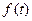 оригинал, а
оригинал, а 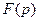 его изображение;
его изображение; 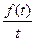 - оригинал
- оригинал 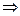
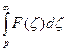 изображение функции
изображение функции 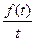 .
.
7) Запаздывание оригинала:
Пусть 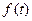 оригинал, а
оригинал, а 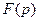 его изображение,
его изображение, 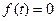 при
при 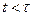
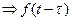 - оригинал, а
- оригинал, а 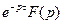 изображение.
изображение.
8) Смещение изображения:
Пусть 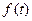 оригинал, а
оригинал, а 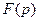 его изображение,
его изображение,
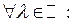
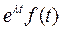 - оригинал, а
- оригинал, а 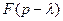 его изображение.
его изображение.
9) Изображение свертки:
Пусть 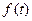 и
и 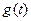 оригиналы,
оригиналы, 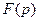 и
и 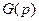 их изображения соответственно, тогда
их изображения соответственно, тогда 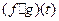 оригинал, а его изображение
оригинал, а его изображение 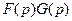 .
.
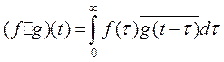
| Оригинал | Изображение |
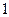
| 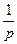
|
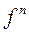
| 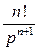
|
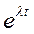
| 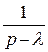
|
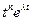
| 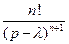
|
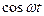
| 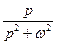
|
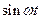
| 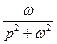
|
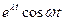
| 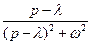
|
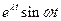
| 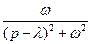
|
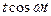
| 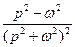
|
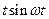
| 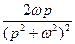
|
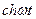
| 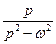
|
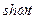
| 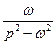
|
 2014-02-24
2014-02-24 361
361








