2014-02-09
482
4.2. Тензор напряжений. Закон Гука. Коэффицинт Пуан сона
Исходя из геометрической схемы для описания результирующей нагрузки необходимо использовать тензор напряжения.
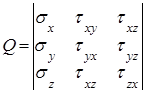
Вектор суммарного напряжения, исходя из данного тензора, может быть представлен в виде трех составляющих:
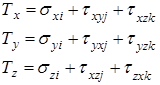
В соответствии с правилом четности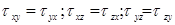 
. Поэтому для описания сложного состояния необходимо не шесть, а только три компонента: 
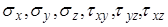. Как известно основной закон сопромата: 
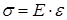, поэтому, учитывая, что действующая нагрузка делится на несколько составляющих, сложное напряжение может быть представлена в виде произведения тензоров:
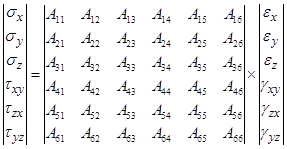
Взаимосвязь между каждыми составляющими тензора напряжения (левая часть) и тензора деформации (правая часть) может быть выражена:
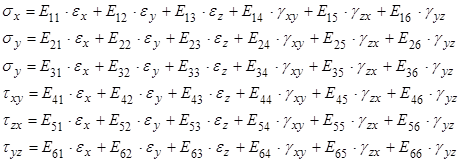
Теоретически для описания Q необходимо 36 упругих постоянных. Благодаря симметричности тензоров, число упругих сокращается до одного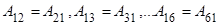 
В этом случае если в изделии имеется ортогональная или косая перекрестная структура, наличие этих плоскостей сокращает количество упругих составляющих до 9, и
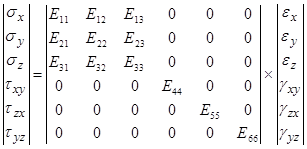
Таким образом описания кассой перекрестной и ортогональной структуры достаточно 9 упругих постоянных в случае однонаправленного композита количество переменных сокращается до 5:
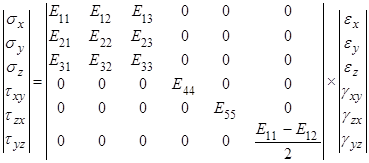
В случае изотропного материала достаточно всего лишь двух упругих постоянных – модуля растяжения и модуля сдвига. Между упруго – деформационными константами и инженерными модулями, определяемых на разрывных машинах, существуют зависимости, позволяющие использовать результаты механических определений для программирования напряжения соответствующего наполнителя, удобнее использовать не величины модулей (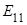
,
,...,
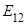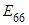), а обратные им величины податливости 
.
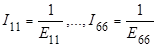Между податливостями и экспериментальными, получаемыми при испытаниях на разрывных машинах, показателями существуют зависимости:
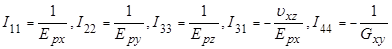
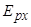- модуль упругости при растяжении в направлении х;
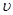- коэффициент Пуансона (отношение деформации в поперечном и продольном разрезе).
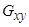- модуль упругости при сдвиге.
