Глава 2 Статистический анализ рядов распределения
Комплексный анализ рядов распределения включает следующие моменты:
- Построения ряда распределения и его графическое представление.
- Расчет показателей центра и структуры распределения.
- Расчет и анализ показателей вариации.
- Характеристика формы распределения (изучение).
- Выравнивание эмпирического распределения и оценка соответствия определенному теоретическому распределению.
Ряд распределения – распределение единиц совокупности по значениям того или иного признака в конкретны условиях места и времени.
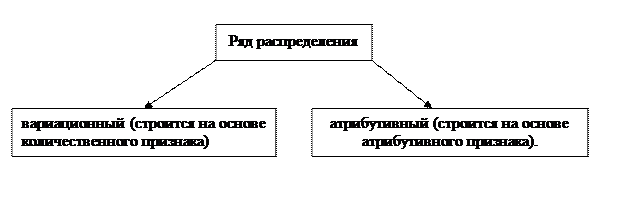
Изучение рядов распределения по количественному признаку позволяет определить типический уровень признака в изучаемой совокупности, определить наличие выбросов и решить вопрос о необходимости их изучения, оценить степень разброса значений признака вокруг типического уровня, изучить структуру совокупности, описать форму распределения, а также подобрать теоретическое распределение, на основе которого можно прогнозировать поведение распределения изучаемого объекта.
Значение признака в рядах распределения называется вариантой (или вариантом).
Число единиц, обладающих тем или иным значением, называют частотой.
Ряды распределения могут быть представлены в табличной форме и графически.
| Значение признака или варианты | Частота, fi | Частость, относительная частота, статистическая вероятность, f|i | Накопленные частоты, ∑ fi | Накопленные частости, ∑ f|i |
| x1 | f1 | f|1 | f1 | f|1 |
| x2 | f2 | f|2 | f1 + f2 | f|1 + f|2 |
| x3 | f3 | f|3 | f1 + f2 + f3 | f|1 + f|2 + f|3 |
| … | … | … | … | … |
| xn | fn | f|n | f1 + f2 + … + fn | f|1 + f|2 + … + f|n |
Первая графа содержит значение признака, если ряд строится по атрибутивному признаку или по дискретному количественному или интервалы значений признака, если ряд строится по непрерывному количественному признаку. В этом случае ряд называется интервальный вариационный ряд.
Вторая графа – частота. Количество единиц совокупности, обладающих данным значением признака.
Третья графа – частость, относительная частота, статистическая вероятность. Отношение числа каждой группы к сумме частот.
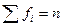
Четвертая графа – сумма накопленных частот. Кумулятивные частоты. Получаются путем последовательного суммирования частот по каждой группе.
Пятая графа – кумулятивные частости. Если сумма накопленных частот равна n, то сумма накопленных частостей равна 1.
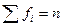 ,
, 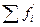
Распределение семей города по величине среднедушевого дохода.
| Группы семей по величине среднедушевого дохода, xi | Число семей, fi | Относительные частоты, 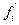
| Накопленные частоты, ∑ fi | Накопленные частости, 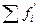
|
| До 1500 | 0,06 | |||
| 1500 – 2500 | 0,07 | |||
| 2500 – 3500 | 0,17 | |||
| 3500 – 4500 | 0,25 | |||
| 4500 – 5500 | 0,22 | |||
| 5500 – 6500 | 0,15 | |||
| 6500 и более | 0,08 | |||
| итого | 1,00 |
 2014-02-09
2014-02-09 516
516








