Классы точности средств измерений.
Классификация погрешностей средств измерений.
Вариация показаний приборов.
Полные входные и выходные сопротивления.
Входное сопротивление определяет реакцию входного сигнала на подключение средств измерения к источнику входного сигнала.
Выходное сопротивление определяет реакцию его выходного сигнала на подключение к выходу средств измерений фиксированной нагрузки.
Подключение средств измерения к источнику сигнала вызывает потребление энергии от объекта измерения. Вследствие этого величина, подлежащая измерению, изменяется и появляется дополнительная погрешность измерения.
В электрических цепях выделяют два основных способа подключения средств измерения к объекту измерения:
1. последовательный – в разрыв цепи;
2. параллельный – параллельно исследуемому участку цепи.
Для уменьшения энергии, потребляемой средством измерения от объекта измерения, необходимо:
Ø при последовательном включении уменьшать входное сопротивление
|
|
|
Ø при параллельном включении увеличивать входное сопротивление.
Вариация – это мера рассеивания наблюдений. Для определения вариации необходимо подойти к заданной точке шкалы с двух сторон. Вариация показаний будет равно их разности.
Вариация показаний измерительного прибора – это разность показаний измерений прибора при установке выбранного значения измеряемой величины: один раз путем её уменьшения, а второй раз – путем её увеличения.
Распределение погрешности из-за вариации считают равномерной в интервале вариации. Истинным значением измерения, при наличии вариации, считают среднее значение от подходов с каждой стороны.
| Классификационный признак | Погрешности средств измерения |
| 1. По составляющим средства измерения | 1) погрешность меры; 2) погрешность преобразования; 3) погрешность сравнения; 4) погрешность фиксации результата сравнения. |
| 2. По условию применения средства измерения: нормальные условия; рабочие условия. | 1) основная погрешность; 2) дополнительная погрешность. |
| 3. По характеру поведения измеряемой величины | 1) статическая погрешность; 2) динамическая погрешность. |
| 4. По способу выражения погрешностей | 1) абсолютная погрешность; 2) относительная погрешность; 3) приведенная погрешность. |
| 5. По характеру проявления | 1) систематическая погрешность; 2) случайная погрешность. |
| 6. По характеру зависимости погрешности от измеряемой величины | 1) аддитивная погрешность; 2) мультипликативная погрешность. |
Пояснение: Аддитивная погрешность – это погрешность, не зависящая от измеряемой величины х. Она определяется смещением нуля усилителя и его дрейфом.
|
|
|
Мультипликативная погрешность – это погрешность, зависящая от измеряемой величины х. Она определяется изменение сопротивления нагрузки и ее нестабильностью.
Класс точности – это обобщенная характеристика точности средств измерений, устанавливаемая только для тех средств измерений, у которых суммарная погрешность, содержащая систематическую и случайную составляющие, нормируется в виде одного предела допускаемой погрешности. Эти пределы могут выражаться в виде абсолютных, относительных и приведенных погрешностей.
1. В форме абсолютной погрешности. Она устанавливается:
1) для одночленной формулы: 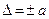
2) для двухчленной формулы: 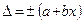
2. В форме относительной погрешности. Она устанавливается:
1) для одночленной формулы:
а) в виде относительной погрешности: 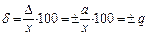
б) в виде приведенной погрешности: 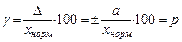
2) для двухчленной формулы – в виде относительной погрешности:
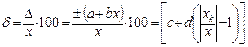
Значения q, p, c, d, применяемые для обозначения класса точности, выбирают из ряда предпочтительных чисел: (1; 1,5; 2; 2,5; (3); 4; 5; 6)·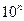 , где n = +1, 0, -1, -2, -3, … Другие значения для обозначения классов точности не используются.
, где n = +1, 0, -1, -2, -3, … Другие значения для обозначения классов точности не используются.
Обозначение классов точности.
| Форма выражения погрешности | Предел допускаемой погрешности | Обозначение класса точности |
| Приведенная погрешность: 1) нормирующее значение выражено в единицах измеряемой величины 2) нормирующее значение принято равным длине шкалы (см) |  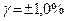 | 1,5 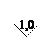 |
| Относительная погрешность 1) постоянна по диапазону 2) возрастает с уменьшением измеряемой величины | 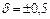 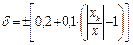 |  0,2/0,1 0,2/0,1 |
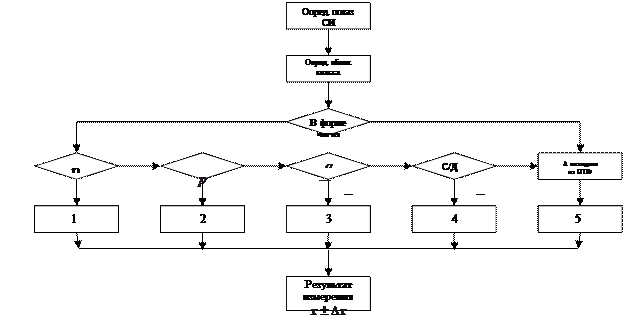
1) 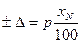 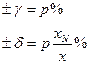 | 2) 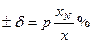 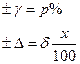 | 3) 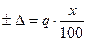 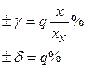 | 4) 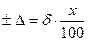 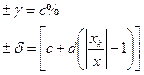 | 5) 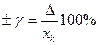 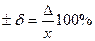 |
 2014-02-09
2014-02-09 1085
1085
