Задачи теории расписаний. Алгоритм Джонсона для двух машин

Имеем конвейер из двух машин: m=2. Каждая работа состоит из двух операций с длительностям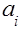и и 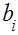, минимизируется общее время обслуживания работ.

Последовательность, минимизирующая общее время работы, такова: сначала запускаются работы, для которых 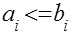в порядке неубывания 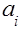, затем все работы, для которых 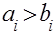в порядке невозрастания 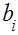(тем самым минимизируем простои 2-ой машины из-за того, что 1-ая еще не успела обработать какую-либо работу). Доказана оптимальность такой последовательности. Однако на случай n>2 результаты не распространяются.

NP -полнота задачи является веским доводом при обосновании необходимости построения приближенных или эвристических алгоритмов ее решения, применения схем направленного перебора вариантов (таких, как метод последовательного конструирования, анализа и отсеивания вариантов (обобщение метода ветвей и границ)), а также при обосновании необходимости исследования частных случаев задачи.

Павловым А. А. и др. предложен следующий путь решения NP -полных задач:

- исследуется труднорешаемая задача и находятся теоретические свойства, которым удовлетворяет ее оптимальное решение;

- на основе этих свойств разрабатывается полиномиальный алгоритм решения, при этом вводится понятие полиномиальной разрешимости задач из класса NP, под которым понимается существование полиномиального алгоритма, удовлетворяющего следующим условиям:

1) если при решении произвольной индивидуальной задачи выполняются определенные аналитические условия, то эта индивидуальная задача решается строго (т.е. получено строго оптимальное решение);

2) в результате работы полиномиального алгоритма всегда известно решена или нет данная индивидуальная задача точно;

3) полиномиальный алгоритм является эффективным и статически значимым, т.е. при моделировании произвольных индивидуальных задач в большинстве случаев полученные решения являются точными.