Задачи теории расписаний. Классификация задач, способы представления.
Задача о назначениях. Венгерский метод
Транспортная задача. Метод северо-западного угла.
Существуют частные типы задач линейного программирования, которые, в силу особой своей структуры, допускают решение более простыми методами. Из них мы остановимся только на одной — так называемой «транспортной задаче» (ТЗ). Она ставится следующим образом: имеются т пунктов отправления (ПО) A1, А2.,..., An, в которых сосредоточены запасы каких-то однородных грузов в количестве соответственно a1, a2,..., am единиц. Имеются п пунктов назначения (ПН) В1, В2,..., Вn, подавших заявки соответственно на b1, b2,..., bn единиц груза. Сумма всех заявок равна сумме всех запасов:
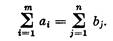 (10.1)
(10.1)
Известны стоимости cij перевозки единицы груза от каждого пункта отправления Ai до каждого пункта назначения Вj (i =l, 2,..., т; j= 1, 2,..., n). Все числа су, образующие прямоугольную таблицу (матрицу), заданы:
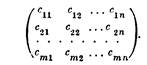 (10.2)
(10.2)
Коротко матрицу (10.2) будем обозначать (cij).
Считается, что стоимость перевозки нескольких единиц груза пропорциональна их числу.
Требуется составить такой план перевозок (откуда, куда и сколько единиц везти), чтобы все заявки были выполнены, а общая стоимость всех перевозок минимальна.
Поставим эту задачу как задачу линейного программирования. Обозначим xij, — количество единиц груза, отправляемого из i -го ПО Ai в j -и ПН Bj. Неотрицательные переменные xij тоже можно записать в виде матрицы
 (10.3)
(10.3)
которую мы будем коротко обозначать (хij). Совокупность чисел (хij) (10.3) мы будем называть «планом перевозок», а сами величины хij — «перевозками». Эти неотрицательные переменные должны удовлетворять следующим условиям.
1. Суммарное количество груза, направляемого из каждого ПО во все ПН, должно быть равно запасу груза в данном пункте. Это даст нам т условий-равенств:
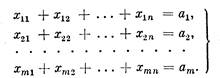 (10.4)
(10.4)
2. Суммарное количество груза, доставляемого в каждый ПН из всех ПО, должно быть равно заявке, поданной данным пунктом. Это даст нам п условий-равенств:
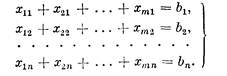 (10.5)
(10.5)
3. Суммарная стоимость всех перевозок, то есть сумма величин хij, умноженных на соответствующие стоимости cij, должна быть минимальной:
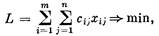 (10.6)
(10.6)
где знак двойной суммы означает, что суммирование производится по всем комбинациям индексов i и j, т. е. но всем парам ПО — ПН.
Мы видим, что перед нами — задача линейного программирования с условиями-равенствами (10.4), (10.5) и минимизируемой линейной функцией (10.6). Особенностью этой задачи является то, что все коэффициенты в условиях (10.4), (10.5) равны единице — это позволяет решать задачу очень простыми способами. О них и пойдет речь.
Прежде всего, замечаем, что условия-равенства (10.4), (10.5) не являются линейно независимыми, так как их правые части связаны условием (10.1). Число линейно независимых среди уравнений (10.4), (10.5) равно не m + n (числу уравнений), а т + п — 1. Общее число переменных xij в нашей задаче равно т • п; как бы ни разрешать уравнения (10.4), (10.5), число базисных переменных будет равно т + п — 1, а число свободных переменных
k = тп – (т + п - 1) = (т - 1) (n - 1).
Мы знаем, что в задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР, в опорной точке, где по крайней мере k переменных равны нулю. Значит, в пашем случае для оптимального плана по крайней мере (m - 1) (n - 1)перевозок должны быть равны нулю (из соответствующих ПО в соответствующие ПН ничего не перевозится).
Будем называть любой план перевозок допустимым, если он удовлетворяет условиям (10.4), (10.5) (все заявки удовлетворены, все запасы исчерпаны). Допустимый план будем называть опорным, если в нем отличны от нуля не более т + п - 1 базисных перевозок, а остальные перевозки равны нулю. План (хij) будем называть оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок (L = min).
В силу особой структуры ТЗ при ее решении не приходится долго и нудно разрешать и пере разрешать систему уравнений. Все операции по нахождению оптимального плана сводятся к манипуляциям непосредственно с таблицей, где в определенном порядке записаны условия транспортной задачи: перечень ПО и ПН, заявки и запасы, а также стоимости перевозок сij. По мере заполнения этой таблицы в ее клетках проставляются сами перевозки xij. Транспортная таблица состоит из т строк и п столбцов. В правом верхнем углу каждой клетки мы будем ставить стоимость сij перевозки единицы груза из Аi в Bj, а центр клетки оставим свободным, чтобы помещать в нее саму перевозку xij. Клетку таблицы, соответствующую пунктам Аi Вj будем кратко обозначать (i, j).
Пример транспортной таблицы, где приведены условия задачи и стоимости перевозок, по нет еще самих перевозок, дан в таблице 10.1, где т = 4, п = 5.
Прежде всего займемся составлением опорного плана.. Это в транспортной задаче очень просто: можно, например, применить так называемый «метод северо-западного угла». Продемонстрируем его непосредственно на конкретных данных таблицы 10.1. Начнем заполнение транспортной таблицы с левого верхнего («северо-западного») угла. Пункт В1 подал заявку на 18 единиц груза; удовлетворим ее из запасов пункта
Таблица 10.1
 пн
по пн
по
| В1 | В2 | В3 | В4 | В5 | Запасы аi |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| Заявки bj |
А 1 После этого в нем остается еще 30 - 18 =12 единиц груза; отдадим их пункту В 2. Но заявка этого пункта еще не удовлетворена; выделим недостающие 15 единиц из запасов пункта A2 и т. д. Рассуждая точно таким же образом, заполним до конца перевозками xi j транспортную таблицу (таблица 10.2). Проверим, является ли этот план допустимым: да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения; значит, все в порядке — все заявки удовлетворены, все запасы израсходованы (сумма запасов равнасумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы).
Здесь и в дальнейшем мы проставляем в таблице только отличные от нуля перевозки, а клетки, соответствующие нулевым перевозкам, оставляем «свободными». Проверим, является ли план перевозок, данный в таблице 10.2, опорным (не слишком ли много там отличных от нуля, «базисных» перевозок?). Число свободных клеток с нулевыми перевозками в таблице 10.2 равно как раз (m-1)(n-1) = 3•4 = 12, так что план — опорный. Вот как нам его удалось легко построить!
 Таблица 10.2
Таблица 10.2
| Пн по | В1 | В2 | В3 | В4 | В5 | Запасы аi |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| Заявки bj |
Теперь пора подумать о том, является ли этот план оптимальным — т. е. минимальна ли для него общая стоимость перевозок? Скорее всего, нет (ведь составляя опорный план, мы совсем не думали о стоимостях). Так и есть — план не оптимальный. Например, сразу видно, что можно его улучшить, если произвести в нем «циклическую перестановку» перевозок между клетками таблицы, уменьшив перевозки в «дорогой» клетке (2.3) со стоимостью 12, но зато увеличив перевозки в «дешевой» клетке (2.4) со стоимостью 6. Чтобы план оставался опорным, мы должны при этом сделать одну из свободных клеток базисной, а одну из базисных — свободной. Сколько единиц груза можем мы перенести по циклу (2.4) → (3.4) → (3.3) → (2.3), увеличивая перевозки в нечетных вершинах цикла и уменьшая — в четных? Очевидно, не больше, чем 11 единиц (иначе перевозки в клетке (3.4) стали бы отрицательными). Очевидно, в результате циклического переноса допустимый план остается допустимым — баланс запасов и заявок не нарушается. Ну что же, произведем этот перенос и запишем новый, улучшенный план перевозок в таблице 10.3.
Теперь посмотрим, чего мы добились, сколько сэкономили? Общая стоимость плана, показанного в таблице 10.2, равна L1 = 18 • 13 + 12 • 7 + 15 • 8+33 • 12 + +9 • 10+11-8+4-10+26-15 =1442;
Таблица 10.3
| ПН ПО | В1 | В2 | В3 | В4 | В5 | Запасы аi |
| А1 | 18 13 | 12 7 | 14 | 7 | 5 | |
| А2 | 11 | 15 8 | 22 12 | 11 6 | 8 | |
| А3 | 6 | 10 | 20 10 | 8 | 11 | |
| А4 | 14 | 8 | 10 | 4 10 | 26 15 | |
| Заявки bj |
Общая стоимость плана, показанного в таблице 10.3, равна L2 = 18∙13 +12.7 +15∙8 + 22∙12 +11∙6 +20∙10+ 4∙10 + 26∙15 = 1398.
Таким образом, нам удалось уменьшить стоимость перевозок на 1442 — 1398 = 44 единицы. Это, впрочем, можно было предсказать и не подсчитывая полную стоимость плана. Действительно, алгебраическая сумма стоимостей, стоящих в вершинах цикла, со знаком плюс, если перевозки в этой вершине увеличиваются, и со знаком минус — если уменьшаются (так называемая «цена цикла»), в данном случае равна: 6 - 8+10 - 12 = - 4. Значит, при переносе одной единицы груза по этому циклу стоимость перевозок уменьшается на четыре. А мы их перенесли целых 11; значит, стоимость должна была уменьшиться на 11∙4 = 44 единицы, что и произошло.
Значит, весь секрет оптимизации плана перевозок в том, чтобы переносить («перебрасывать») перевозки по циклам, имеющим отрицательную цену.
В теории линейного программирования доказывается, что при опорном плане для каждой свободной клетки транспортной таблицы существует цикл, и притом единственный, одна вершина которого (первая) лежите данной свободной клетке, а остальные — в базисных клетках. Поэтому, отыскивая «выгодные» циклы с отрицательной ценой, мы должны высматривать — нет ли в таблице соблазнительных, «дешевых» свободных клеток. Если такая клетка есть, нужно для нее найти цикл, вычислить его цену и, если она будет отрицательной, перенести по этому циклу столько единиц груза, сколько будет возможно (без того, чтобы какие-то перевозки сделать отрицательными). При этом данная свободная клетка становится базисной, а какая-то из бывших базисных — свободной. Очевидно, это равносильно «переразрешению» системы уравнений относительно других базисных переменных, по делается это гораздо легче.
Попробуем еще раз улучшить план, приведенный и таблице 10.3. Например, нас «соблазняет» дешевая клетка (1.5) со стоимостью 5. Нельзя ли улучшить план, увеличив перевозки в этой клетке, зато, уменьшив в других (при этом, конечно, придется кое-где перевозки тоже увеличить). Давайте разглядим внимательно таблицу 10.3 и найдем в пей цикл, первая вершина которого лежит в свободной клетке (1.5), а остальные — все в базисных клетках.' Немного подумав, мы этот цикл обнаружим: это последовательность клеток (1.5)  (4.5)
(4.5)  (4.4)
(4.4)  (2.4)
(2.4)  (2.2)
(2.2)  (1.2) (и замыкая цикл, снова возвращаемся в (1.5)). Нечетные вершины цикла отмечены плюсом — это значит, что перевозки в этих клетках увеличиваются: четные — знаком минус (перевозки уменьшаются). Цикл показан стрелками в таблице 10.4.
(1.2) (и замыкая цикл, снова возвращаемся в (1.5)). Нечетные вершины цикла отмечены плюсом — это значит, что перевозки в этих клетках увеличиваются: четные — знаком минус (перевозки уменьшаются). Цикл показан стрелками в таблице 10.4.
Подсчитаем цену этого цикла. Она равна 5 – 15 + 10 – 6 + 8 - 7= - 5. Так как цена цикла отрицатель-па, то переброска перевозок по этому циклу выгодна. Посмотрим, сколько же единиц мы можем по нему перебросить? Это определяется наименьшей перевозкой, стоящей в отрицательной вершине цикла. В данном случае это опять 11 (чистое совпадение!). Умножая 11 па цепу цикла — 5 получим, что за счет переброски 11 единиц груза по данному циклу мы еще уменьшим стоимость перевозок на 55 (предоставляем любознательному читателю сделать это самостоятельно).
Таким образом, разыскивая в транспортной таблице свободные клетки с отрицательной ценой цикла и перебрасывая по этому циклу наибольшее возможное количество груза, мы будем все уменьшать и уменьшать стоимость перевозок. Бесконечно уменьшаться она не может (она никак не может стать меньше нуля!), значит, рано или поздно мы придем к оптимальному плану. Для такого плана уже не остается ни одной свободной клетки с отрицательной ценой цикла. Это — признак того, что оптимальное решение найдено.
Таблица 10.4
 ПН
ПО ПН
ПО
| B1 | B2 | B3 | B4 | B5 | Запасы аi |
| A1 |
  12- 12-
|
 + +
| ||||
| A2 |
 15+ 15+
|
 - -
| ||||
| A3 | ||||||
| A4 |
 4+ 4+
| -26 | ||||
| Заявки bj |
В теории линейного программирования существуют способы, позволяющие автоматически, без размышлений, выделять свободные клетки с отрицательной ценой цикла (так называемый «метод потенциалов»), но мы на них останавливаться не будем, так же как и на ряде других способов решения транспортной задачи, с которыми читатель может ознакомиться, но специальным руководствам [5, 7, 8].
В заключение скажем несколько слов о так называемой «транспортной задаче с неправильным балансом», когда сумма заявок не равна сумме запасов:
 (10.7)
(10.7)
Если  (сумма запасов больше суммы заявок), то все заявки могут быть удовлетворены, но при этом не все запасы будут израсходованы. Задача может быть сведена к транспортной задаче с правильным балансом, если ввести в рассмотрение некий «фиктивный» пункт назначения Вф, условно приписав ему заявку, равную избытку запасов над заявками:
(сумма запасов больше суммы заявок), то все заявки могут быть удовлетворены, но при этом не все запасы будут израсходованы. Задача может быть сведена к транспортной задаче с правильным балансом, если ввести в рассмотрение некий «фиктивный» пункт назначения Вф, условно приписав ему заявку, равную избытку запасов над заявками:
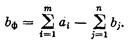 (10.8)
(10.8)
Тогда задача сводится к задаче с правильным балансом, так как
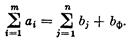 (10.9)
(10.9)
Возникает вопрос: а каковы же стоимости перевозок из пунктов отправления Ai в «фиктивный» пункт назначения Bф? Естественно положить их равными нулю (ведь фактически в пункт Вф ничего перевозиться не будет!). Поэтому для любого пункта отправления стоимость сiф = 0.
Введем в транспортную таблицу дополнительный столбец, соответствующий пункту назначения Вф, и проставим в нем нулевые стоимости перевозок. После этого задача решается как обычная транспортная, и для нее находится оптимальный план перевозок:

При этом нужно иметь в виду, что все перевозки хiф, стоящие в правом столбце, фактически никуда не отправляются, а остаются на пунктах отправления Ai.
Может встретиться также случай 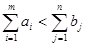
(запасов не хватает для удовлетворения всех заявок);
в этом случае можно тем или другим способом «срезать» заявки и снова получить транспортную задачу с правильным балансом. Если нас совершенно не интересует, насколько «справедливо» удовлетворяются заявки, а важно только «подешевле развезти» имеющиеся запасы (все равно, куда), то можно ввести в рассмотрение фиктивный пункт отправления Аф, условно приписав ему недостающий запас, равный
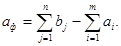
Подробнее на этих вопросах мы останавливаться не будем (см. [6]).





21..Задача коммивояжера. Метод ветвей и границ










23.Программирование на сетях. Основные понятия теории графов 





 |
25.Программирование на сетях. Упорядочивание вершин графа.
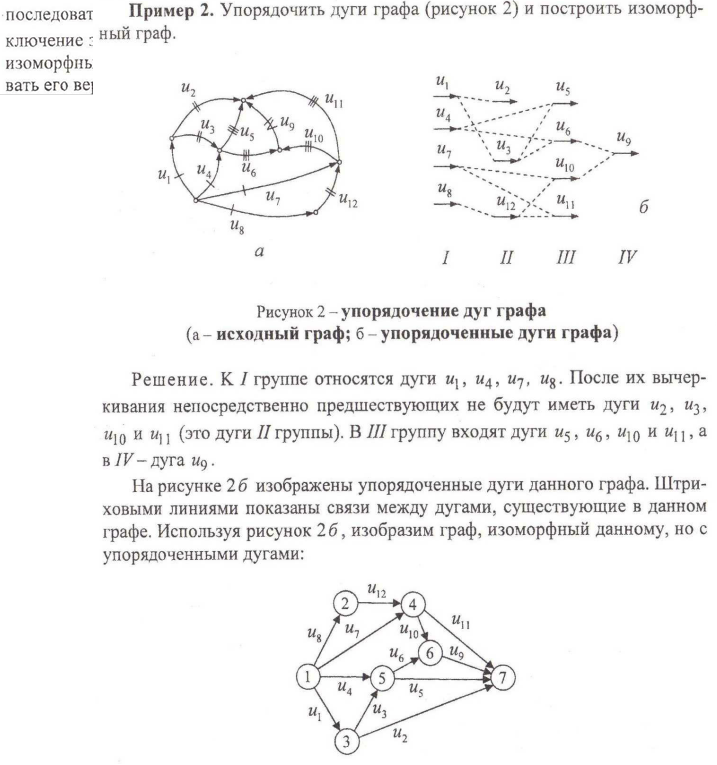
26.Программирование на сетях. Алгоритм Фалкерсона. Упорядочение дуг графа

27. Программирование на сетях. Потоки на сетях. Разрез на сети. Теорема Форда-Фалкерсона
 |



28.Программирование на сетях. Постановка и алгоритм решения задачи о максимальном потоке. 

29.Программирование на сетях. Приложения задачи о максимальном потоке.
 |
 |
30. Задача о потоке минимальной стоимости

Задача теории расписаний считается заданной, если определены
1) подлежащие выполнению работы и операции;
2) количество и типы машин, выполняющих операцию;
3) порядок прохождения машин;
4) критерии оценки расписаний.
В зависимости от характера поступления работ различают два вида задач: статические и динамические. В статических задачах в свободную систему одновременно поступает определенное число работ. После этого новые работы не поступают и расписание составляется для вполне определенного и известного заранее числа работ. В динамических задачах работы поступают в систему в некоторые моменты времени, которые можно предсказать только в статистическом смысле. Поэтому моменты будущих поступлений не определены. Упорядочение в динамических и статических задачах требует различных методов решения.
Порядок выполнения машинами операций одной работы определяет, является ли система машин:
а) конвейерной;
б) со случайным порядком выполнения работ;
в) системой произвольного типа.
В конвейерной системе последовательность прохождения машин одинакова для каждой из работ. Согласно принятой терминологии это означает, что существует такая нумерация машин, что для одной и той же работы номер машины, выполняющей операцию X, меньше номера машины, выполняющей операцию Y, если X предшествует Y.
В системе со случайным порядком выполнения работ машинами любая операция может выполняться любой машиной, т.е. все машины являются идентичными.
В системах произвольного типа каждая операция может выполняться какой-либо определенной машиной.
Для классификации задач теории расписаний в дальнейшем используется запись А/В/С/D, где
· А характеризует процесс поступления работ. Для динамических задач А представляет собой функцию распределения времени между поступлениями. Для статических задач А соответствует числу одновременно поступивших работ, если по этому поводу ничего специально не оговорено. Если на месте А стоит n то это означает произвольное, но конечное число работ в статическом случае.
· В характеризует число машин в системе. Если на месте В стоит m то это означает произвольное число машин.
· С характеризует порядок (дисциплину) выполнения работ машинами. Если на месте С находится F, то это соответствует конвейерной системе; если R - то случайной, и если G - произвольной. Для системы, состоящей из одной машины, указанные дисциплины теряют смысл и поэтому для такой системы третий параметр опускается.
· D характеризует оценку (критерий) расписания.
Пример употребления указанных обозначений: запись 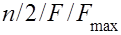 означает, что требуется упорядочить n работ для выполнения их в конвейерной системе, состоящей из двух машин, так, чтобы минимизировать максимальную длительность прохождения работы (джонсоновская задача составления расписания).
означает, что требуется упорядочить n работ для выполнения их в конвейерной системе, состоящей из двух машин, так, чтобы минимизировать максимальную длительность прохождения работы (джонсоновская задача составления расписания).
Общая задача теории расписаний записывается так: 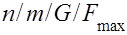 - упорядочить
- упорядочить  работ в произвольной системе из
работ в произвольной системе из  машин так, чтобы минимизировать максимальную длительность прохождения работы.
машин так, чтобы минимизировать максимальную длительность прохождения работы.

32.Задачи теории расписаний. Одноприборные задачи ТР. Минимизация суммарного запаздывания.






33.Задачи теории расписаний. n-приборные задачи ТР. Постановка задачи, ограничения
 |



 2014-02-24
2014-02-24 3881
3881