Двойственная задача линейного программирования
Ая итерация
План можно улучшить. Вводимой переменной будет х6, а выводимой х5
3-ая итерация
План улучшить нельзя, так как в индексной строке нет отрицательных элементов, следовательно найден оптимальный план.
X*=(0;0;11/2;035;0;1)
Оптимальное значение целевой функции берем в индексной строке в колонке «план» (в последнем разделе), Так как исходная целевая функция стремилась к min, то у полученного значения целевой функции из последнего раздела меняется знак на противоположный т.е.:
F*=-68
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается в том, что решение одной из них может быть получено из решения другой.
Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции
F = C1X1 + C2X2+…+CnXn (1)
при условиях
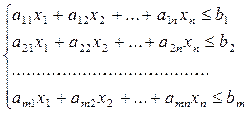 (2)
(2)
xj≥0 (j=1,n) (3)
Задача, состоящая в нахождении минимального значения функции
F*=b1y1+b2y2+…+bmym (4.)
при условиях
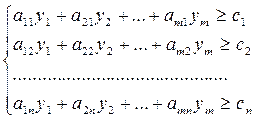 (5)
(5)
yi≥0 (i=1,m) (6)
называется двойственной задачей по отношению к задаче (1) – (3)..
Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственной парой.
Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Целевая функция исходной задача задается на max, а целевая функция двойственной задачи на min.
2. Матрица:
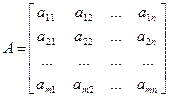
составленная из коэффициентов при неизвестных в система ограничений (2) исходной задачи и аналогичная матрица
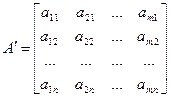
в двойственной задаче получаются друг из друга транспонированием(т.е. заменой строк столбцами, а столбцов – строками).
3. Число переменных в двойственной задаче равно числу соотношений в системе (2) исходной задачи, а число ограничений в системе(5) двойственной задачи равно числу переменных в исходной задаче.
4. Коэффициентами при неизвестных целевой функции двойственной задачи являются свободные члены системы (2) исходной задачи, а правыми частями в системе ограничений двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи.
5. Если переменная xj исходной задачи может принимать лишь положительные значения, то j-тое условие в системе (5) двойственной задачи является неравенством вида «≥». Если же переменная xj может принимать как положительные так и отрицательные значения, то j-тое соотношение в системе (5) является уравнением.
6. Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-тая переменная двойственной задачи yi≥0. В противном случае переменная yi может принимать как положительные так и отрицательные значения.
Двойственные пары задач обычно подразделяются на симметричные и несимметричные.
В симметричной паре двойственной задачи ограничения вида (2) исходной задачи и соотношения (5) двойственной задачи являются неравенствами вида «≤», т.е переменные обеих задач могут принимать только неотрицательные значения.
Он требует, чтобы задача была задана в виде основной задачи линейного программирования. Вместе с тем его можно применять при решении задач линейного программирования, у которых свободные члены системы ограничений могут быть любыми числами(как положительные, так и отрицательные).
Пусть требуется определить max значения функции:
F=C1X1+C2X2+…+CnXn →max
при условиях:
x1p1+x2p2+…+xmpm+xm+1pm+1+…+xnpn= po,
где:
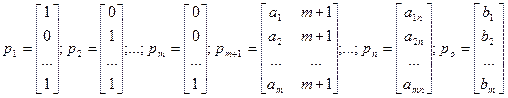
xj≥0 (j=1,n)
Таким образом, векторы р1;p2; …;pm – единичные векторы, образующие базис.
Среди чисел bi имеются отрицательные (i=1,m).
В данном случае решение X = (b1, b2, …,bm, 0, 0, …,0) является решением системы линейных уравнений, представляющих решение исходной задачи, но не является решением самой исходной задачи.
Такое решение Х называют псевдопланом (т.к. по условию xj≥0, а среди bi есть отрицательные числа.)
Рассмотрим алгоритм двойственного симплекс-метода:
1. Составляют симплекс-таблицу и находят псевдоплан задачи.
2. Проверяют псевдоплан на оптимальность или устанавливают неразрешимость задачи. Если в колонке «План» нет отрицательных чисел, то псевдо план является оптимальным. Если отрицательные числа имеются, то переходят к новому псевдоплану, либо устанавливают неразрешимость задачи.
3. Выбирают направляющую строку путем определения наибольшего по модулю отрицательного числа в колонке «План». Затем определяют направляющий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов «m+1»-ой строки к соответствующим отрицательным элементам направляющей строки.
В результате определяют вектор, выводимый из базиса и вектор, вводимый в базис.
4. Находят новый псевдоплан путем пересчета элементов нового раздела симплекс-таблицы и повторяют все действия с пункта 2.
Пример: найти максимальное значение функции
F=-x1+x2+x3 →max
при условиях:
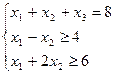
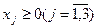
 2014-02-24
2014-02-24 1301
1301
