Шаг4.
Шаг3.
Шаг2.
Шаг1.
Симплекс-метод для решения задач линейного программирования
Графический метод решения задач линейного программирования прост и нагляден. Однако, практическое его применение ограничивается задачами, в которых всего две переменных величины. Если условие задачи линейного программирования непротиворечиво, то область её допустимых решений образует выпуклый многогранник в n-мерном пространстве. При этом оптимальное решение, если оно существует, обязательно достигается, в некоторой вершине многогранника (возможно и более чем в одной).
Таким образом, чтобы найти решение задачи линейного программирования достаточно перебрать лишь вершины многогранника области допустимых решений и определить точку (вершину), соответствующую оптимальному решению. Однако, в сложных задачах число вершин может оказаться очень большим, поэтому перебор всех вершин будет затруднен.
Симплекс-метод позволяет осуществить упорядоченный перебор вершин многогранника.
Симплекс-метод позволяет решать задачу линейного программирования, если она задача в виде основной задачи линейного программирования. Если же ограничения имеют вид неравенств, то необходимо от неравенств перейти к равенствам путем введения дополнительных неотрицательных переменных.
Пусть n-количество основных переменных, m- количество дополнительных переменных, тогда N=n+m – число переменных преобразованной системы ограничения.
Затем все переменные задачи должны быть разделены на базисные, число которых равно m (количество уравнений системы) и свободные,число которых равно k. Причем, базисные переменные и целевая функция должны быть выражены через свободные. При этом не следует смешивать свободные переменные с основными, а базисные с дополнительными.
Разделение переменных задачи линейного программирования, то есть отыскание первого базисного решения (первого базиса), довольно сложная задача. Наиболее просто такое разделение переменных на базисные и свободные можно произвести в случае, когда K=N-m=n.
Допустим, что решение задачи линейного программирования существует, причем, оптимальное значение целевой функции конечно.
Рассмотрим алгебру симплекс-метода:
Выбрать «m» переменных, задающих первоначальное допустимое решение системы уравнений (базисное решение). Свободные переменные приравнять к 0. Найти значение базисных переменных.
Проверить, нельзя ли за счет одной из свободных переменных улучшить значение целевой функции, придавая этой переменной отличные от нуля положительные значения. Если это возможно, перейти к шагу 3, в противном случае вычисления прекратить.
Найти предельное значение переменной, за счет которой можно улучшить значение целевой функции. Улучшение значения этой переменной допустимо до тех пор, пока одна из «m» базисных переменных не обратится в 0. Эту переменную исключают из целевой функции и базисного решения, и вводят ту переменную, за счет которой результат может быть улучшен
Разрешить систему «m» - уравнений относительно новых базисных переменных. Исключить эти переменные из целевой функции и вернутся к шагу 2.
Исследование опорного плана на оптимальность, а также весь вычислительный процесс в симплекс –методе целесообразно вести в таблице.
В качестве исходного опорного плана задачи принимаем x1=0,x2=0, …, xk=0, xk+1=b1, xk+2=b2, …, xk+m=bm
Рассмотрим заполнение симплекс таблицы:
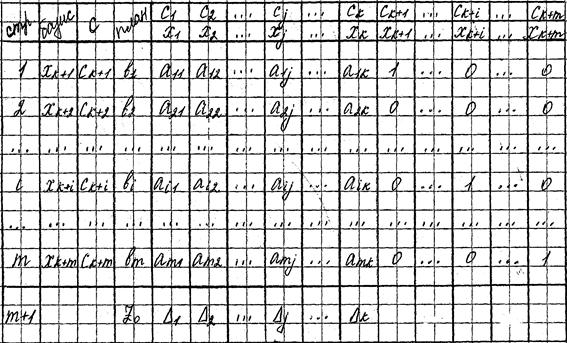
В столбце «Базис» записываются переменные, входящие в базис, т.е. базисные переменные.
В столбце «С» записываются коэффициенты при неизвестных целевой функции, являющихся базисными переменными.
В столбце «План» записывают положительные компоненты исходного опорного плана.
В самой верхней строке таблицы записаны коэффициенты целевой функции.
Первые «m» строк таблицы определяются исходными данными задачи: это коэффициенты при переменных в уравнениях-ограничениях.
Показатели «m+1» вычисляются.В столбце «План» записывают значение целевой функции при данном опорном плане, а в столбцах «Xj»- значения Δj=Zj-Cj
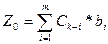
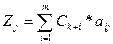
(j=1,k)
После заполнения таблицы, исходный опорный план проверяется на оптимальность. Для этого просматривают элементы (m+1)-ой строки таблицы. В результате может быть иметь место один из 3-х случаев:
1. Δj≥0 (j=1,k) - в этом случае опорный план является оптимальным
2. Δj<0 – для некоторых j, но все коэффициенты aij в столбце Δj≤0. Это означает, что целевая функция не ограничена сверху на множестве планов.
3. Δj<0 – для некоторых индексов j и для каждого такого j, по крайней мере, одно из чисел aij >0. Это означает, что можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится.
Переход от одного опорного плана к другому осуществляется исключением из исходного базиса одной переменной и введением в него новой.
В качестве переменной, вводимой в базис, выбирают ту, которой в строке «m+1» соответствует наибольшее по модулю отрицательное число (например, aij).
Для определения переменной, подлежащей исключению из базиса, находят
min 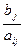 всех aij >0 (j=1,m)
всех aij >0 (j=1,m)
Пусть этот min достигается в R-той строке, тогда из базиса будет исключена переменная xk+r и введена на ее место переменная xj.
Число arj называют направляющим (разрешающим) элементом, а соответствующие ему строка и столбец – направляющими.
Затем находится новый опорный план, т.е. заполняется новый раздел симплекс-таблицы.
Прежде всего заполняется строка вводимой переменной xj.
Новые элементы этой строки определяются путем деления элементов r-той строки исходного опорного плана на направляющий элемент
В столбце «С» r-той строки нового опорного плана проставляется коэффициент целевой функции, соответствующий новой вводимой переменной.
Пересчитаем столбец «план». r-ая строка уже заполнена, в столбце «план»
там стоит число br/arj.
Пересчет остальных элементов данного столбца ведут по правилу треугольника (правилу 3-х чисел)
Для этого находят три числа:
1. Число, стоящее в предыдущем разделе симплекс-таблицы на месте искомого элемента нового раздела таблицы.
2. Число, стоящее в предыдущем разделе симплекс-таблицы на пересечении строки, в которой находится искомый элемент новой симплекс- таблицы, и столбца, соответствующего переменной, вводимой в базис.
3. Число, стоящее в новом разделе симплекс -таблицы на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимой в базис переменной (выделенной строки)
Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс- таблице, а третье – числу, находящемуся в новой симплекс – таблице.
Для определения искомого элемента новой симплекс – таблицы из первого числа вычитают произведение второго и третьего.
После заполнения столбца «План» пересчитывают матрицу коэффициентов, используя рассмотренное выше правило треугольника. Переменным, входящим в базис, всегда соответствуют в матрице коэффициентов единичные векторы - столбцы. Определяют элементы «m+1» строки нового опорного плана (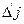 ).
).
Если все элементы Δ ́j =Z ́j – Cj ≥ 0, то новый опорный план является оптимальным.
Если же среди указанных чисел имеются отрицательные, то используя описанную выше последовательность действий, находят новый опорный план.
Процесс продолжают о тех пор, пока либо не получат оптимальный план задачи, либо не установят ее неразрешимость.
Итак, нахождение оптимального плана симплекс-метода включает следующие этапы:
1. Находят опорный план.
2. Составляют симплекс-таблицу.
3. Выясняют, имеется ли хотя бы одно отрицательное число Δ j. Если нет, то найденный план оптимален, если есть, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.
4. Находят направляющую строку и столбец.
Направляющий столбец определяется наибольшим по модулю отрицательным числом Δ j, а направляющая строка – минимальным из отношений столбца «план» и положительных элементов направляющего столбца.
5. Определяют положительные элементы нового опорного плана.
6. Проверяют найденный план на оптимальность. Если план не оптимальный, то возвращаются к пункту 4, а если план оптимален или установлена неразрешимость, то процесс решение задачи закончен.
Пример №1.
Найти решение задачи линейного программирования
Z = x1 + 3x2 →max при ограничениях:
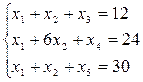
xj ≥0 (j=1,5)
Рассматриваемый алгоритм симплекс- таблицы требует, чтобы задача была приведена к виду ОЗЛП: ограничения заданы в виде системы уравнений, а целевая функция стремилась к максимуму.
Составим симплекс-таблицу:
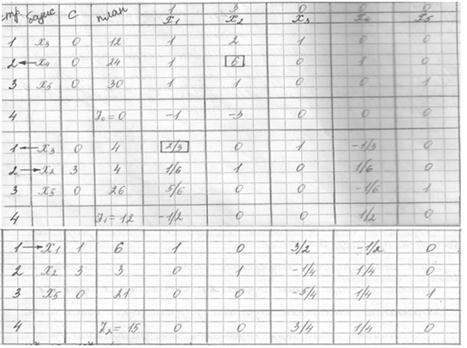
В первый раздел симплекс-таблицы записываем матрицу коэффициентов системы ограничений.
Выбираем базисные переменные, ими будут те переменные, вектора которых в совокупности образуют единичную матрицу. У нас это х3, х4, х5.
Заполняем вторую и третью колонку симплекс-таблицы.
В колонку «план» записываем столбец свободных членов.
Заполняем индексную (4) строку, и по ней ведем анализ.
В этой строке есть отрицательные элементы, а в соответствующих им столбцам есть положительные элементы. Следовательно,план можно улучшить.
Выбираем max по модулю отрицательный элемент, ему соответствует переменная х2, ее будем вводить в базис.
Определим выводимую переменную.
Находим min:
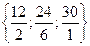 =4 соответствует х4
=4 соответствует х4
х3 х4 х5
Значит выводим из базиса х4
Разрешающий элемент а22=6
Переходим к заполнению второго раздела симплекс-таблицы
Первой заполняется вторая строка (выделенная строка). ее элементы находятся путем деления элементов разрешающей строки первого раздела на разрешающий элемент.
Пересчет всех остальных элементов этого раздела ведем по правилу трех чисел.
Вновь анализируем индексную строку и видим, что план можно улучшить.
Вводимой переменной будет х1, а выводимой будет х3 .
Заполнение элементов третьего раздела ведем аналогично.
В индексной строке третьего разделяя все Δj≥0, следовательно, процесс вычисления закончен, найдено оптимальное решение задачи:
Z* = 15 X* = (6;3;0;0;21)
Симплекс-таблица позволяет контролировать процесс вычислений, начиная со второго раздела.
Элементы всех строк этого раздела пересчитываются по правилу трех чисел (кроме выделенной строки), а для контроля элементы индексной строки находят так же, как и в первом разделе. Если значения совпали, то ошибок нет.
Пример 2.
Найти решение задачи линейного программирования
Z = 2x1 − 6x2 +5х5→max при ограничениях:
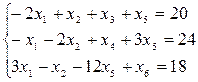
xj ≥0 (j=1,6)
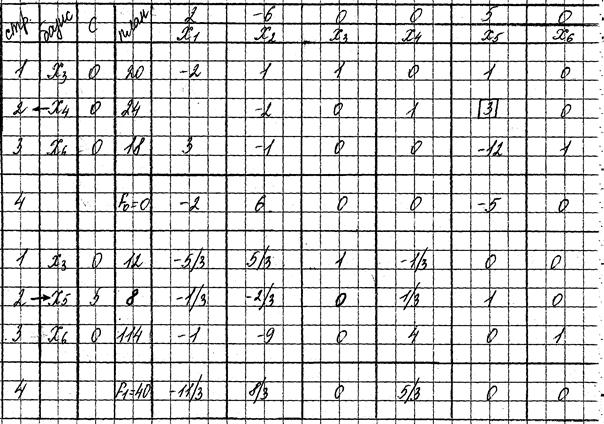
I-ая итерация.
Вводим х5, т.к max |-aij|=|-5|
Выводим х4, т.к min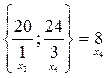
II-ая итерация
Анализ четвертой строки показывает, что задача оптимального решения не имеет. Целевая функция не ограничена сверху, т.к в индексной строке есть отрицательный элемент, а в соответствующем ему столбце нет положительных.
Для построения исходного опорного плана при решении задачи симплекс-методом необходимо, чтобы матрица коэффициентов при переменных, имеющая «m» строк и «n» столбцов (m<n), содержала в себе единичную матрицу порядка «m». Такая матрица получалась после введения дополнительных переменных в исходные ограничения вида «≤». Однако, если исходные ограничения задаются сразу уравнениями, то нет никакой гарантии, что матрица коэффициентов содержит единичную матрицу порядка «m». То же относится и к системе неравенств вида «≥».
Дополнительные переменные входят в такую систему с коэффициентами «-1». В этих случаях для решения задачи применяется симплекс-метод с искусственным базисом.
В левую часть уравнений вводятся неотрицательные искусственные переменные ω1, ω2, …, ωm, коэффициенты при которых образуют единичную матрицу. Эти же переменные с большими по абсолютной величине отрицательными коэффициентами (-M) включаются в целевую функцию.
В результате расширенная задача принимает вид:

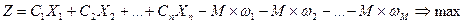
При условиях:
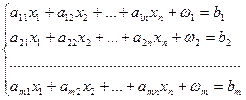
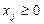 ,
, 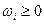
Искусственные переменные необходимы для построения исходного плана задачи. В процессе решения они должны выводиться из базиса, т.к. в окончательном плане задачи должны соблюдаться исходные уравнения, а это возможно когда ωi=0.
Решение задачи линейного программирования методом искусственного базиса включает следующие этапы.
1. Составляют расширенную задачу.
2. Находят опорный план расширенной задачи.
3. С помощью обычных вычислений симплекс-методом исключают искусственные переменные из базиса. Анализ ведут по «m+2» строке. В результате находят опорный план исходной задачи, либо устанавливают ее неразрешимость.
4. Используя найденный опорный план исходной задачи симплекс-методом находят оптимальный план (анализ ведут по «m+1» строке) или устанавливают неразрешимость задачи.
Возможны случаи, когда при оптимизации опорного плана расширенной задачи в «m+2» строке еще остается отрицательное число, но в соответствующем ему столбце нет положительных коэффициентов, следовательно, в базисе остаются несколько искусственных переменных и они не могут быть выведены. Это означает, что исходная задача не имеет искомого решения. Полученный план не удовлетворяет всем поставленным условиям, и окончательный базис будет содержать искусственную переменную.
Пример:
Найти оптимальное решение задачи
F=-2x1+3x2−6x3−x4→min
при ограничениях
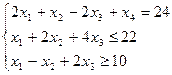
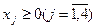
Приведем задачу к виду основной задачи линейного программирования, учитывая, что целевая функция должна стремиться к max
:
F=-2x1+3x2−6x3−x4→max
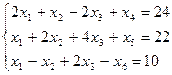
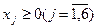
Среди векторов, составленных из коэффициентов при неизвестных, только два единичных (х4 и х5), поэтому в левую часть третьего уравнения добавим искусственную переменную ω и составим расширенную задачу:
F=-2x1+3x2−6x3−x4−М ω →max
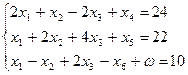
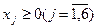
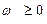
Теперь задача содержит необходимое количество единичных векторов, образующих базис. Составим симплекс –таблицу
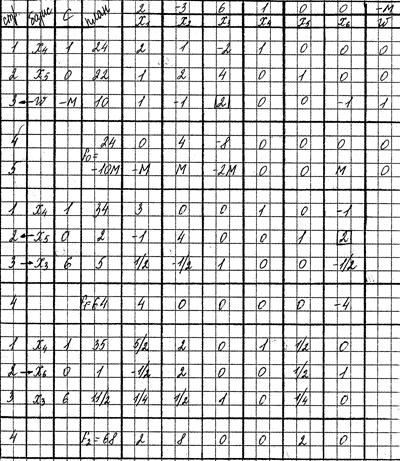
1-ая итерация
План можно улучшить. Анализ ведем по второй индексной строке. Вводимой переменной будет х3,а выводимой ω т.к.
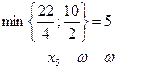
Примечание.
Искусственную переменную всегда стараются вывести первой. Как только ω выведена из базиса, на последующих итерациях столбец ω не заполняется и индексная строка будет одна.
 2014-02-24
2014-02-24 3668
3668
