Шаг четвертый
Шаг третий
Шаг второй
Шаг первый
Поиск кратчайшего пути в графе
Поиск кратчайшего пути в графе между двумя точками - это нахождение такой последовательности дуг (или дуги), ведущей от начальной точки до конечной, при которой сумма их весов будет минимальной.
Рассмотрим задачу поиска кратчайшего пути между двумя заданными вершинами S и t для случая неотрицательной матрицы весов.
Наиболее эффективный алгоритм решения такой задачи создал Дейкстра. Этот метод основан на приписывании вершинам временных пометок, причем, пометка вершины дает верхнюю границу длины пути от S к этой вершине. Эти пометки (их величины) постепенно уменьшаются с помощью итерации, и на каждом шаге итерации только одна извременных пометок становится постоянной. Это означает, что эта пометка дает точную длину кратчайшего пути от S к рассматриваемой вершине
Рассмотрим суть алгоритма Дейкстры.
Пусть l(Xi) - пометка вершины Xi.
Присваивание начальных значений
Положить 1(S) = 0 и считать эту пометку постоянной.
Положить l(Xi) = ∞ для всех Xi ≠ S, и считать эти пометки временными.
Положить р = S,
где р- вспомогательная величина, равная номеру той вершины, которая на данном шаге получает постоянную пометку.
Обновление пометок
Для Х є Г(р), пометки которых временные, изменить их в соответствии со следующим выражением:
l(Xi)=min[ l(Xi); l(p)+c(p,Xi) ] (1)
Превращение пометки в постоянную
Среди всех вершин с временными пометками найти такую, для которой l(Xi*)=min[l(Xi)]
Считать пометку вершины Xi* постоянной и положить p =Xi*.
а) Если надо найти путь от S к t:
- если p = t, то 1(р) является длиной кратчайшего пути, конец задачи;
- если р ≠ t, то перейти ко второму шагу.
б) Если требуется найти путь от S ко всем остальным вершинам:
- если все вершины отмечены как постоянные, то пометки этих вершин дают длины кратчайших путей, конец задачи;
- если некоторые пометки являются временными, перейти ко второму шагу.
-
Длина кратчайшего пути от исходной вершины S к любой вершине графа t равна величине постоянной пометки этой вершины t, т.е. l(S,t)=l(t ).
Для нахождения самого пути воспользуемся соотношением:
l(Xi*)+c(Xi*,Xi)=l(Xi), (2)
где Xi* - вершина, непосредственно предшествующая вершине Xi в кратчайшем пути от S к t
Если условие (2) выполняется, то дуга (Xi*,Xi) входит в кратчайший путь.
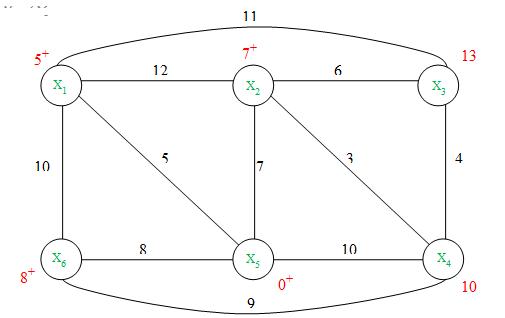
Используя изложенный выше алгоритм, определим кратчайший путь в графе G от заданной вершины Х5 ко всем вершинам.
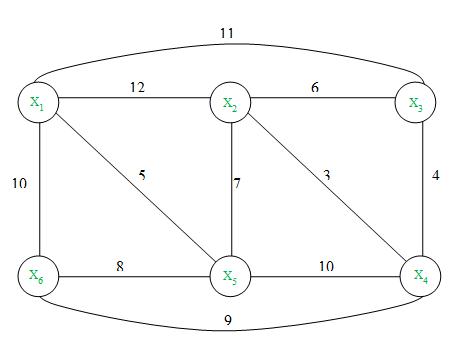
Шаг1 Присвоим начальные пометки вершинам:
l(X5) = 0+;
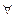 Xi ≠ X5, l(Xi) = ∞;
Xi ≠ X5, l(Xi) = ∞;
p = X5,
Первая итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X5) = {X1, X2, X4, X6}
обновляем пометки вершин X1, X2, X4, X6
l(X1) = min{l(X1); l(p) + c(p(X1))} = min {∞, 0+5} = 5
l(X2) = min{l(X2); l(p) + c(p(X2))} = min {∞, 0+7} = 7
l(X4) = min{l(X4); l(p) + c(p(X4))} = min {∞, 0+10} = 10
l(X6) = min{l(X6); l(p) + c(p(X6))} = min {∞, 0+8} = 8
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{5, 7, ∞, 10, 8} = 5 соответствует Х1=> l(X1*)= 5+
p= X1
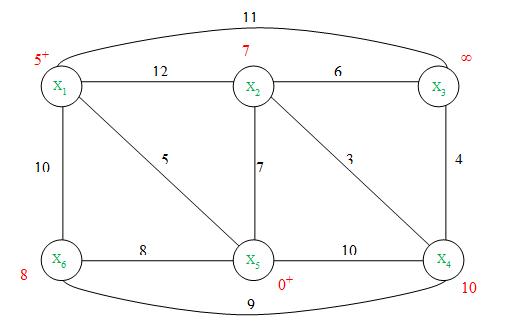
Так как не все вершины имеют постоянные пометки, то переходим к следующей итерации
Вторая итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X5) = {X2, X3, X5, X6}
Так как вершина X5 имеет постоянную пометку, то ее не рассматриваем.
l(X2) = min{l(X2); l(p) + c(p(X2))} = min {7, 5+12} = 7
l(X3) = min{l(X3); l(p) + c(p(X3))} = min {∞, 5+11} = 16
l(X6) = min{l(X6); l(p) + c(p(X6))} = min {8, 5+10} = 8
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{7, 16, 10, 8} =7 соответствует X2 => l(X2*)= 7+
p= X2
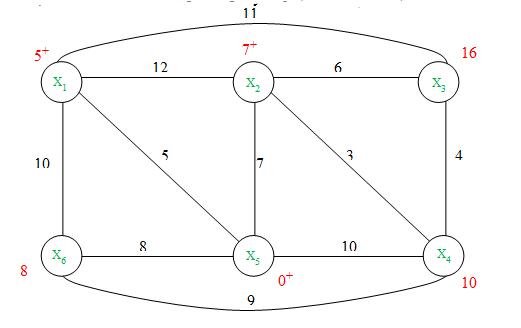
Так как не все вершины имеют постоянные пометки, то переходим к следующей итерации
Третья итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X5) = {X1, X3, X4, X5}
Так как вершины X1 и X5 имеет постоянные пометки, то их не рассматриваем.
l(X3) = min{l(X3); l(p) + c(p(X3))} = min {16, 7+6} = 13
l(X4) = min{l(X4); l(p) + c(p(X4))} = min {10, 7+3} = 10
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{13, 10, 8} = 8 соответствует X6=> l(X6*) = 4+
p= X6
Так как не все вершины имеют постоянные пометки, то переходим к следующей итерации.
Четвёртая итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X6) = {X1, X4, X5}
Так как вершины X1 и X5 имеет постоянные пометки, то их не рассматриваем.
l(X4) = min{l(X4); l(p) + c(p(X4))} = min {10, 8+9} = 10
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{13, 10} = 10 => l(X4*)= 5+
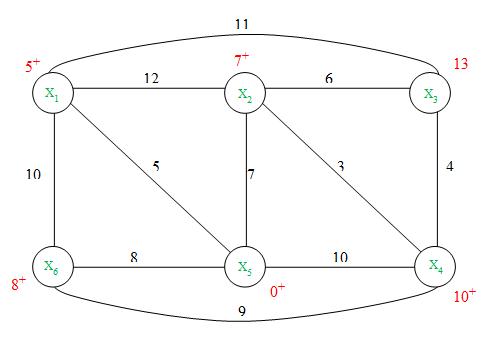
Так как вершина X3 единственная вершина с временной пометкой, то на этой итерации считаем l(X3*)= 13
Так как все вершины имеют постоянные пометки, то итерационный процесс закончен. Пометки вершин дают точную длину кратчайшего пути от исходной вершины X5 ко всем вершинам.
Определим сами кратчайшие пути в графе. Для этого используется соотношение:
l(Xi*)+c(Xi*,Xi)= l(Xi),
Пусть Хi = X1, ей предшествуют вершины X2; X3; X5; X6
l(X2) + c(X2, X1) = 7 + 12 = 19 ≠ l(X1)
l(X3) + c(X3, X1) = 13 + 11 = 24 ≠ l(X1)
l(X5) + c(X5, X1) = 0 + 5 = 5 = l(X1)
l(X6) + c(X6, X1) = 8 + 10 = 18 ≠ l(X1)
Следовательно, дуга (X5, X1) входит в кратчайший путь
1) Пусть Хi = X2, ей предшествуют вершины X1; X3; X4; X5
l(X1) + c(X1, X2) = 5 + 12 = 17 ≠ l(X2)
l(X3) + c(X3, X2) = 13 + 6 = 19 ≠ l(X2)
l(X4) + c(X4, X2) = 10 + 3 = 13 ≠ l(X2)
l(X5) + c(X5, X2) = 0 + 7 = 7 = l(X2)
Следовательно, дуга (X5, X2) входит в кратчайший путь
2) Пусть Хi = X3, ей предшествуют вершины X1; X2; X4
l(X1) + c(X1, X3) = 5 + 11 = 16 ≠ l(X3)
l(X2) + c(X2, X3) = 7 + 6 = 13 = l(X3)
l(X4) + c(X4, X3) = 10 + 4 = 14 ≠ l(X3)
Следовательно, дуга (X2, X3) входит в кратчайший путь
3) Пусть Хi = X4, ей предшествуют вершины X2; X3; X5; X6
l(X2) + c(X2, X4) = 7 + 3 = 10 = l(X4)
l(X3) + c(X3, X4) = 13 + 4 = 17 ≠ l(X4)
l(X5) + c(X5, X4) = 0 + 10 = 10 = l(X4)
l(X6) + c(X6, X4) = 8 + 9 = 17 ≠ l(X4)
Следовательно, дуги (X2, X4) и (X5, X4) входят в кратчайший путь
4) Пусть Хi = X6, ей предшествуют вершины X1; X4; X5
l(X1) + c(X1, X6) = 5 + 10 = 15 ≠ l(X6)
l(X4) + c(X4, X6) = 10 + 9 = 19 ≠ l(X6)
l(X5) + c(X5, X6) = 0 + 8 = 8 = l(X6)
Следовательно, дуга (X5, X6) входит в кратчайший путь
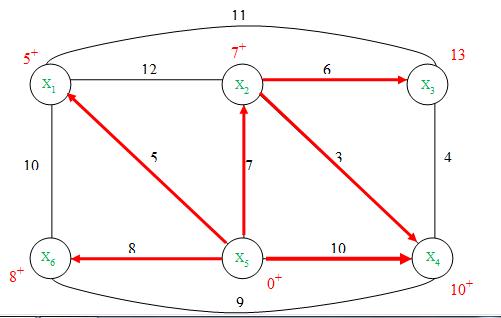
Таким образом, в кратчайший путь от вершины X5 ко всем вершинам входят дуги:
- к вершине X1: (X5, X1) вес пути = 5;
- к вершине X2: (X5, X2) вес пути = 7;
- к вершине X3: (X5, X2) (X2, X3) вес пути = 13;
- к вершине X4: (X5, X2) (X2, X4) вес пути = 10;
или (X5, X4) вес пути = 10;
- к вершине X6: (X5, X6) вес пути = 8;
На графе все кратчайшие пути выделены красными линиями
 2014-02-24
2014-02-24 612
612








