Тема 2. 4. Динамическое программирование

Задача о максимальном потоке

Поиск максимального потока в графе

Одной из наиболее важных задач в теории графов является задача определения максимального потока, протекающего от некоторой вершины S графа (истока) к некоторой конечной вершине t (стоку). При этом каждый дуге (x_i, x_j) графа G приписана некоторая пропуская способность C_ij, и эта пропуская способность определяет наибольшее значение потока, который может протекать по данной дуге. Эта задача и её варианты возникают во многих практических приложениях, например, при определении максимальной интенсивности транспортного потока между двумя пунктами по карте дорог, представленных графом. Решая эту задачу, можно указать также ту часть сети дорог, которая «насыщена» и образует «узкое место» в отношении потока между двумя указанными концевыми пунктами.

Метод решения задачи о максимальном потоке от S к t был предложен Фордом и Фалкерсоном, и их «техника пометок» составляет основу других алгоритмов решения многочисленных задач указанного типа.

Рассмотрим задачу определения максимального потока между выделенными узлами связной сети. Каждая дуга сети обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего по данной дуге. Ориентированная (односторонняя) дуга соответствует нулевой пропускной способности в запрещенном направлении.

Пропускную способность C_ij сети можно представить в матричной форме.

Алгоритм решения:

Шаг1:
Найти цель, соединяющую источник S и сток t, по которой поток принимает положительное значение. В направлении S→t. Если такой цели не существует, перейти к шагу 3. В противном случае перейти к шагу 2.

Шаг 2:

Пусть 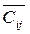(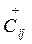) – пропускные способности дуг цепи (S,t) в направлении S→t(t→ S).

ϴ= min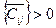

Матрицу пропускных способностей C=[C_ij] изменить следующим образом:

а) вычесть ϴ из всех ;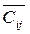

б) прибавить ϴ ко всем .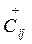

Заменить текущую матрицу С на вновь полученную и перейти к шагу 1. Операция (а) дает возможность использовать остатки пропускных способностей дуг выбранной цепи в направлении S→t.

Операция (б) восстанавливает исходные пропускные способности сети, т.к. уменьшение пропускной способности дуги в одном направлении можно рассматривать как увеличение ее пропускной способности в противоположном направлении.

Шаг 3:

Найти максимальный поток в сети.

Пусть C=[C_ij]- исходная матрица пропускных способностей.

C*=[C*_ij] – последняя матрица, получившаяся в результате модификации исходной матрицы (шаг 1 и 2).

Оптимальный поток Х=[x_ij] в дугах задается так:

X_ij =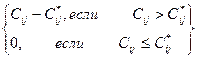

Максимальный поток из S в t равен:

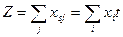
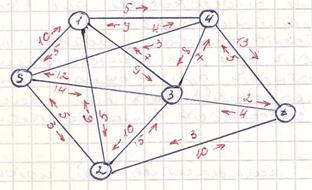
Пример: определить максимальный поток в графе

S 1 2 3 4 t

C =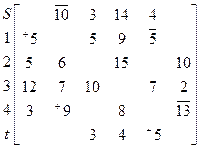

I итерация

Шаг 1.

В качестве исходной цепи выберем S→1→4→t. Тогда ячейки (S,1),(1,4),(4,t) помечаем знаком (−), а ячейки (1,S),(4,1),(t,4) помечаем знаком (+).

Максимальный поток для этой цепи равен

ϴ= min{C_s1, C₁₄, C_4t}=min{10, 5, 13}=5

Можно выбрать различные исходные цепи. Хороший выбор должен давать наибольшее значение ϴ. Но может возникнуть много вариантов таких цепей. При программировании цепь удобно определять непосредственно из матрицы С, начиная с первой строки S-строки и выбирая следующий узел среди тех, которые соединены с S положительным потоком. Далее рассматривается строка, соответствующая выбранному узлу, и выбирается следующий узел, соединенный с предыдущим положительной дугой. Процесс продолжается до тех пор, пока не будет достигнут узел t.

Корректируем матрицу С, вычитая ϴ= 5 из всех элементов, помеченных (−), и складывая со всеми элементами, имеющими знак (+). Получаем новую матрицу.

Аналогичные действия производим и на последующих итерациях.

II итерация

S 1 2 3 4 t

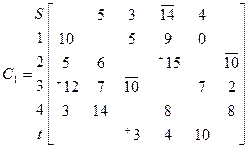
Выберем цепь (S→3→ 2→ t)

ϴ= min{14, 20, 10}=10 Скорректируем матрицу С

III итерация.

S 1 2 3 4 t

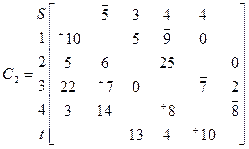
Выберем цепь (S→1→3→4→t)

ϴ= min{5, 9, 7, 8}=5 Скорректируем матрицу С

IV итерация

S 1 2 3 4 t

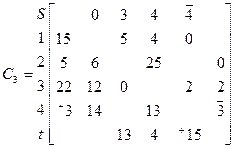
Выберем цепь (S→4→t)

ϴ= min{4, 3}=3 Скорректируем матрицу С

V итерация

S 1 2 3 4 t

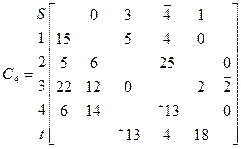
Выберем цепь (S→3→t)

ϴ= min{4, 2}=2 Скорректируем матрицу С

VI итерация

S 1 2 3 4 t

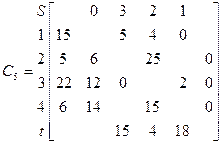
Между S и t нельзя построить цепь,т.к все элементы в столбце t равны нулю. Таким образом получим матрицу С*

Построим матрицу Х. Отрицательные элементы в матрице заменим нулями.

S 1 2 3 4 t

Х=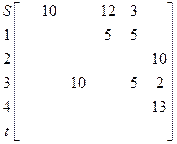

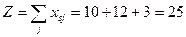
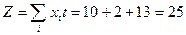
∑ ϴ= 5+10+5+3+2=25

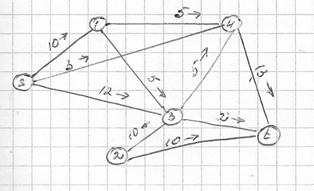
Графически решение представлено графом: