Исполнительный этап

Ориентировочный этап

а) У. Найдите угол между прямой А ₁ С и плоскостью грани АВСD (рисунок 4).

Учащиеся интуитивно определяют этот угол, как угол между прямыми А ₁ С и АС.

У. А почему искомым углом является именно угол между прямыми А ₁ С и АС, а ни какой-либо другой угол, например, угол между прямыми А ₁ С и BC?

Учащиеся затрудняются ответить.

У. Ваше затруднение объяснимо, так как понятие угла между прямой и плоскостью для вас новое. Тема сегодняшнего урока: «Угол между прямой и плоскостью», запишите тему в тетради.

б) У. Задача нашего урока – изучить понятие угла между прямой и плоскостью. Что для этогонеобходимо сделать?

О. Дать определение данного понятия и разработать алгоритм нахождения угла между прямой и плоскостью.

У. Верно, кроме того, мы изучим свойство данного угла.

а) У. Для определения понятия угла между прямой и плоскостью, нам понадобится следующее определение:

Определение. Ортогональной проекцией прямой на плоскость называется проекция этой прямой на данную плоскость в случае, когда прямая проектирования перпендикулярна этой плоскости.

У. Запишите его в тетрадь. Рассмотрим пример: ортогональной проекцией прямой A ₁ C на плоскость грани ABCD (рис. 4) является прямая AC, здесь прямая проектирования AA ₁ перпендикулярна плоскости ABC. Назовите ортогональную проекцию прямой А ₁ С на плоскость грани

1) DCC ₁ D ₁;

2) ADD ₁ A ₁;

3) ВСС ₁ В ₁, ответ объясните

О. 1) прямая CD ₁; 2) прямая A ₁ D; 3) прямая СВ ₁;

У. Повторите определение (вызывает ученика). А теперь сформулируем определение понятия угла между прямой и плоскостью.

Определение. Углом между прямой и плоскостью называется угол между прямой и её ортогональной проекцией на данную плоскость.

У. Запишите это определение, повторите его. Рассмотрим примеры:

Задачи на готовых чертежах.

№1. Найдите угол между прямой А ₁ С и плоскостью грани ВСС ₁ В ₁ (рисунок 4).

№2. Вычислите градусную меру угла между прямой ВА ₁ и плоскостью грани А ₁ В ₁ С ₁ D ₁ (рисунок 4).

У. Как вы считаете, почему за угол между прямой и плоскостью взят именно угол между прямой и её ортогональной проекцией?

О. Возможно, он обладает какими-то особенными свойствами?

У. Правильно. Давайте проведём не большое наблюдение.

Слайд с 3D моделью (рисунок 5) на котором изображена плоскость α и прямая а пересекающая данную плоскость в точке О. Также проведена ортогональная проекция a₁ прямой а на плоскость α и некоторая произвольная прямая b лежащая в этой плоскости и проходящая через точку О. Затем, прямая b вращается в плоскости α (положение прямой изменяется в интерактивном режиме) и при этом учащиеся видят изменение градусной меры угла между прямыми b и а. Учащиеся замечают, что этот угол является наименьшим в случае, когда прямая b совпадает с прямой а₁.

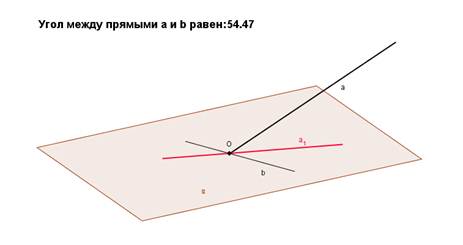
Рисунок 5.

У. Какую гипотезу можно сформулировать на основании данного наблюдения?

О. Угол между прямой и её ортогональной проекцией наименьший среди углов, образованных данной прямой с прямыми, лежащими в плоскости α и проходящими через точку О.

У. Позже мы докажем эту гипотезу.

б) У. Вернёмся к нахождению угла между прямой и плоскостью. Какие действия вы выполняли для нахождения данного угла? Что необходимо сделать в первую очередь?

О. Построить ортогональную проекцию прямой на плоскость.

У. Что необходимо сделать для построения ортогональной проекции?

О (с помощью учителя). На прямой выбрать точку, не принадлежащую плоскости, удобную для того, чтобы её ортогонально спроектировать её на плоскость. Затем, через две точки (точку пересечения исходной прямой с плоскостью и точку, которая является ортогональной проекцией выбранной точки на данную плоскость) провести прямую. Эта прямая и будет ортогональной проекцией прямой на плоскость.

У. Какой следующий шаг?

О. Найти угол между прямой и её ортогональной проекцией на плоскость.

У. Применим данным алгоритм для решения следующей задачи:

Задача. АВСDS – правильная четырёхугольная пирамида. Найдите угол между прямой SC и плоскостью (BSD).

O

D

S

А

В

Решение.

У. Согласно алгоритму, какой шаг необходимо

выполнить первым?

О. Найти ортогональную проекцию прямой SC

на плоскость (BSD).

У. Какую точку удобнее выбрать для проекти-

С

рования?

О. Точку C.

У. Назовите проекцию точки C на плоскость

(BSD).

О. Точка О, так как отрезок CО перпендикулярен плоскости (BSD).

У. Назовите ортогональную проекцию прямой SC на плоскость (BSD).

О. Прямая SO.

У. Какой последний шаг в алгоритме?

О. Нахождение угла между прямой и её ортогональной проекцией.

У. Назовите угол между прямой SC и плоскостью (BSD).

О. Угол СSO.

с) У. Ранее, мы сформулировали гипотезу о свойстве угла между прямой и плоскостью. Сформулируем её в виде теоремы и докажем эту теорему.

Теорема. Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.

M

P

H

O

α

b

a 1

Рисунок 6.

У. Что нам дано по условию теоремы?

О. Прямая а пересекающая плоскость α в точке О; проекция а₁ прямой а на плоскость α; некоторая прямая b лежащая в плоскости и проходящая через точку О (рисунок 6).

У. Что необходимо доказать?

О. что угол между прямыми а и а₁ меньше угла между прямыми а и b.

У. Возможен ли случай, когда угол между прямыми а и b равен 90⁰ ?

О. Возможен.

У. Рассмотрим этот случай подробнее. Может ли угол между прямыми а и а₁ быть больше 90°?

О. Нет. Так как за угол между двумя пересекающимися прямыми берётся наименьший из двух смежных углов образованных данными прямыми. При этом, очевидно что прямая а не перпендикулярна прямой а₁. Следовательно угол между прямыми а и а₁ всегда меньше 90⁰.

У. Рассмотрим случай, когда прямые а и b не перпендикулярны. Как сравнить рассматриваемые углы?

О. Найти содержащие их треугольники.

У. Необходимо дополнительное построение. Из некоторой точки М прямой а проведём перпендикуляры МН и МР на прямые а и b соответственно. Мы не можем сравнить градусные меры углов. Но как можно сравнить углы прямоугольных треугольников?

О. Можно сравнить значения тригонометрических функций от этих углов.

У. Какую тригонометрическую функцию удобнее всего рассмотреть в нашем случае?

О. Функцию sin.

У. Найдите синусы углов МОН и МОР

О. МН / МО, МР / МО.

У. Сравните полученные дроби.

О. МР / МО > МН / МО, так как МН – перпендикуляр, опущенный из точки М к плоскости α, а МР - наклонная. Следовательно, МР > MH.

У. Какой можно сделать вывод о значениях синусов углов и о градусных мерах углов?

О. Синус угла МОН меньше синуса угла МОР. Так как на интервале (0°, 90°) функция у = sin x возрастает, то, угол МОН меньше угла MOP.

У. Именно это и требовалось доказать. Повторите, пожалуйста, формулировку теоремы.

4. Подведение итогов усвоения знаний путём фронтального опроса.

У. Итак, с какими понятиями мы сегодня познакомились?

О. С понятием ортогональной проекции прямой на плоскость, понятием угла между прямой и плоскостью.

У. Какую информацию о понятии угла между прямой и плоскостью узнали?

О. Его определение, алгоритм построения этого угла, его свойство.

У. Дайте определение угла между прямой и плоскостью.

У. Сформулируйте теорему о свойстве угла между прямой и плоскостью.

У. Сформулируйте алгоритм нахождения угла между прямой и плоскостью