Оо
Оо
Э
Dx
Dy
X
Рис. 3: Слева: график касательной, справа: график дифференциала
В жизни мы часто пользуемся дифференциалами для приближенных оценок. Например, если на покраску одного метра забора у Тома Сойера ушел один час, то на покраску еще двух уйдет примерно еще два часа; здесь мы не учитываем возможное изменение скорости покраски, свя-заппое с усталостью, изменением качества краски, наступлением жары и т.н. Или, если вчера нам удалось купить килограмм раков за 25 рублей, то мы ожидаем, что сегодня мы сможем купить 2 килограмма примерно за 50 рублей.
Геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке M(x,y).
Свойства дифференциала:
1. dC = 0,
2. d(Cy) = Cdy,
3. d(u + v) = du + dv,
| 4. d (uv ,(u 5. d |
udv + vdu, vdu udv
v 6. df v u) = f'(u)du.
Глава 5
Прилож:ения производной к исследованию графиков
5.1 Теорема Лагранж:а
Теорема 28 (теорема Лагранжа). Пусть функция f удовлетворяет следующим условиям:
(a) f непрерывна на отрезке [ a, Ь];
(b) f дифференцируема на интервале (a, Ь).
Тогда существует но крайней мере одна такая точка ^ G (a, &) (внутри интервала!), в которой производная равна отнотпепию приращения функции к приращению аргумента на этом отрезке, т. е.
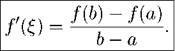
Доказательство. Теорема утверждает, что существует точка (^, в которой угловой коэффициент касательной f '(<^) такой же как у секущей к = tga = ъ-а ■> '^- ^- касательная параллельна секущей. Возьмем прямую, паралл - ьную секущей, и будем её опускать (поднимать) до тех пор, пока она не коснется графика, точка касания и будет точка ^. П
Заключение теоремы Лагранжа может быть записано и в виде:
| f (&) - f (a) | = f (6 | • (6 - a) |
| Ъ = x + ∆ x) | ||
| f(x + ∆ x) - | f (x) = | f (i) ∆ x |
Такие формы записи называют формулами конечных приращений Лагранжа. Ср. с формулой (4.4).
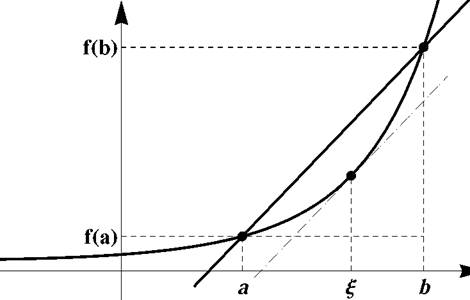
Рис. 1: Геометрический смысл числа ь- - a ^ идея геометрического доказательства теоремы Лагранжа
5.2 Нахож:дение промеж:утков монотонности
Говорят, что функция f строго возрастает на интервале (a,b), если для любых x 1 ,x 2 G (a,b) ИЗ x1 < x 2 следует, что f(x1) < f (x 2). Говорят, что функция f строго убывает на интервале (a,b)^ если для любых x 1, x 2 G (a, b) из x 1 < x 2 следует, что f(x1) > f(x2).^' Функцию называют монотонной^ если она либо возрастает, либо убывает.
Теорема 29 (достаточное условие монотонности). Если производная f полож:ительиа внутри интервала (a, b), то функция f возрастает на этом интервале. Если производная f отрицательна внутри интервала (a,b), то функция f убывает на этом интервале.
Геометрическая интерпретация этой теоремы: если касательные к кривой на некотором промежутке направлены под острыми углами к оси абсцисс, то функция возрастает, если иод тупыми, то убывает. См. правый рис. 1.
Доказательство. Докажем, к примеру, первое утверждение. Рассмотрим два значения x1 и x2 из данного промежутка (a, b). Пусть x2 > x1.
^^Этот тип возрастания и убывания называют строгим.
Докажем, что f (x 2) > f(x1). Для функции f иа отрезке [ x 1 ,x 2] выполняются условия теоремы 28 (Лагранжа), поэтому
f(x2) - f(x1) = f (ξ) • (x2 - x1),
где x1 < ξ < x2j т. е. ξ принадлежит промежутку, па котором произ
водная положительна, откуда следует, что f (x 2) - f(x1) > 0 и, значит,
f (x 2) > f(x1). П
Необходимое условие мопотоппости более слабое. Если функция возрастает на некотором промежутке (a, b), то производная неотрицательна на этом промежутке: f'(x) > 0, x G (a, b), т. е. в отдельных точках производная монотонной функции может равняться нулю.
Пример 25. Найти интервалы монотонности функции y = x2 - 4 x + 3.
Решение. Имеем y' = 2x - 4. Очевидно y' > 0 при x > 2 и y' < 0
при x < 2, т. е. функция убывает на интервале (- оо, 2) и возрастает па
интервале (2, оо), где x 0 = 2 — абсцисса вершины параболы. П
5.3 Нахож:дение локальных экстремумов
Точку x 0 называют точкой (нестрогого локального) максимума функции f, если в некоторой окрестности точки x 0 выполняется неравенство f(x) < f(x0).
Точку x1 называют точкой (нестрогого локального) минимума функции f, если в некоторой окрестности точки x1 выполняются неравенство
f ( x) > f (x 1)-
Для максимума и минимума функции используют общее название
экстремум. Значения функции в точках экстремума называют соответственно Максимум,ом, и минимум,ом, функции.
Теорема 30 (необходимое условие экстремума). Для того чтобы функция f имела экстремум в точке x 0, необходимо, чтобы выполнялось хотя бы одно из следующих трех условий:
(a) f'(x0) = 0; см. рис. 10;
(b) f'(x0) не существует; см. рис. 9;
(c) x 0 — крайняя точка области определения; см. рис. 12. Пример 26. y = x 2, y = \x\, y = л x, y = x3.
Точки, в которых выполнено необходимое условие экстремума, т. е. производная равна нулю или не существует, а также крайние точки, называют критическими (или подозрительными па экстремум). В силу теоремы 30 все точки локального экстремума находятся среди критических, по, как показывает пример y = x"^ (см. рис. 10), могут быть и лишние. Поэтому все критические точки надо проверить — действительно в них есть экстремум или нет. Это делают с помощью теоремы 31.
Теорема 31 (первое достаточное условие экстремума). Пусть f дифференцируема. Если при переходе через точку xq производная меняет знак, то xq — точка локального экстремума. При этом если знак меняется с плюса на минус, то xq — точка максимума, а если знак меняется с минуса на плюс, то xq — точка минимума. Если при переходе через точку xq производная не меняет знак, то xq не является точкой локального экстремума.
Доказательство. Пусть производная меняет знак с плюса на минус, т. е. на некотором интервале (a, xq) производная положительна (f'(x) > 0), а па некотором интервале (x о, b) — отрицательна (f'(x) < 0). Тогда в соответствии с достаточным условием монотонности функция f возрастает на интервале (a,x о) и убывает па интервале (x о ,b).
По определению возрастающей функции f(xo) > f(x) при всех x G
(a, xq), а по определению убывающей функции f(x) < f(xo) при всех x G
(xо,b), т. е. f(xo) > f(x) при всех x G (a, b). Следовательно, xq — точка
локального максимума функции y = f(x). Аналогично рассматривается
случай, когда производная меняет знак с минуса на плюс. П
Теорема 32 (второе достаточное условие экстремума). Пусть f дваясды дифференцируема. Если f'(xo) = 0, а f"(xo) > 0 положительна, то xq есть точка минимума; если f'(xo) = 0 и f"(xo) < 0, то xq — точка максимума.
5.4 Наиболыпее и наименыпее значение функции на отрезке
Точку xq G [ a, b] называют точкой {глобального) максимума функции y = f(x) на отрезке [a,b], если f(x) < f(xo) для всех x G [a,b]. Точку xi G [a,b] называют точкой (глобального) минимума функции y = f(x) на отрезке [a, b], если f(x) > f(xi) для всех x G [ a, b]. При этом значения
f(xo) и f (xi) называют наибольшим, [наименьишм) значением функции y = f(x) на отрезке [ a, b ].
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.
1. Вычислить ироизводную y' = f'(x).
2. Выписать критические точки функции, т. е. точки x, в которых f'(x) = 0 или f'(x) не существует, а также крайние точки области определения.
3. Вычислить значения функции в критических точках (включая крайние точки области определения).
4. Выбрать из этих значений наибольшее и наименьшее.
Задача 22. Найдите наименьшее и наибольшее значение функции y = (9 - x)лx на отрезке [0; 16].
Решение. Действуем но схеме. 1. Вычисляем производную:
y ' = (9 - x) лx + (9 - x)(лx) = -лx + (9-x
x • 2л x + (9 - x) -2x + 9 - x 9 - 3 x
2\[x 2\/x 2\/x
2. Находим критические точки функции. Сначала находим точки, в которых f'(x) = 0:
93x
= 0 ^^ 9 - 3 x = 0 ^^ x = 3.
x
Затем находим точки, в которых f'(x) пе суш,ествует. Такой является точка x = 0, где знаменатель 2л/x обращается в ноль. Добавляем к ней крайние точки области определения x = 0 и x = 16. (Точка x = 0 уже была учтена ранее.) Итак, имеем три критические точки: x = 0, x = 3 и
x = 16.
3. Вычисляем значения функции в точках x = 0, x = 3 и x = 16:
f (0) = (9 - 0)^/0 = 0, f (3) = (9 - 3)\/3 = 6\/3 f«6 • 1, 7 = 10, 2, f (16) = (9 - 16)\/16 = - 7 • 4 = - 28.
4. Выбираем наибольшее и наименьшее из найденных значений. Оче
видно, наибольшим значением является а наименьшим------ 28.
Ответ: Наибольшее значение равно а наименьшее------ 28. П
5.5 Нахож:дение промеж:утков выпуклости
Функцию f называют выпуклой вверх на интервале (a, b) или просто выпуклой^ если выполнено одно из следующих двух эквивалентных условий^^
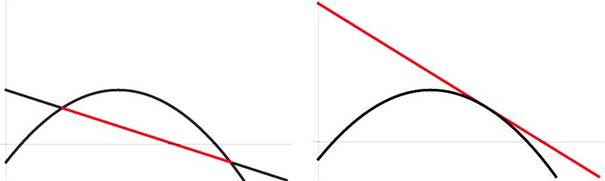
Ф секущая, проведенная через любые две точки x 1 ,x 2 G (a, b), расположена под графиком функции,
Ф касательная, проведенная через любую точку x 0 G (a,b), находится над графиком функции.
|
Рис. 2: Два определения выпуклости вверх
Аналогично определяется выпуклость вниз или вогнутость. Точку, где меняется нанравление выпуклости, называют точкой перегиба.
Теорема 33 (достаточное условие выпуклости). Пусть f дважды дифференцируема. Если вторая производная f" ноложительна внутри интервала (a,b), то функция f выпукла вниз па этом интервале. Если вторая производная f" отрицательна внутри интервала (a,b), то функция f выпукла вверх па этом интервале.
ТОТ тип выпуклости называют строгим.
|
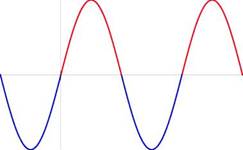
Рис. 3: Перегиб — смена направления выпуклости
Теорема 34 (достаточное условие перегиба). Пусть f дважды дифференцируема. Если при переходе через точку x 0 вторая производная f" меняет знак, то x 0 — точка перегиба.
5.6 Асимптоты графика функции
Асимптотой графика функции y = f(x) называют прямую, обладающую тем свойством, что расстояние от точки (x, f(x)) до этой прямой стремится к нулю при удалении точки графика от начала координат. Асимптоты бывают трех видов: вертикальные, горизонтальные, наклонные. Нахождение асимптот основано на теоремах 35 и 36.
Теорема 35. Для того чтобы прямая x = x 0 была вертикальной асимн-тотой графика функции y = f(x), необходимо и достаточно, чтобы был равен бесконечности хотя бы одни из следуюгцих пределов:
lim f (x)
x→x 0
lim f (x)
x→x 0+0
lim f (x)
x→x 0 - 0
(двусторопияя асимптота), (иравосторопияя асимптота), (левосторонняя асимптота).
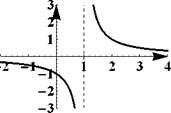
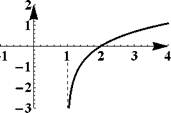
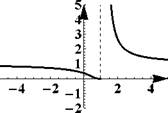
Пример 27. На рис. 4 показаны вертикальные асимптоты графиков функ
| y |
| ции y |
| ex- 1 |
ln(x 1
ж - 1 y
Правило: вертикальные асимптоты следует искать только на концах области определения функции.
Замечание 1. В силу теоремы 6 первый предел сугцествует тогда и только тогда, когда второй и третий пределы существуют и равны между
|
|
|
Рис. 4: Примеры вертикальных асимптот
собой. Отсюда правило: если удалось посчитать первый предел, то считать второй и третий уже ие имеет смысла — они такие же. А если оказалось, что второй и третий пределы пе равны или один из них пе существует, то пе имеет смысла считать первый — оп пе существует.
Еще одно правило: Если xq не попадает в ОДЗ функции f из-за того, что зпамепатель обращается в ноль, то следует начать с вычисления первого предела.
Теорема 36. Для того чтобы прямая y = kx + b была наклонной асимптотой графика функции y = f(x), необходимо и достаточно, чтобы существовали два предела:
lim f (x) lim f (x)
ж^ - оо x
k, lim (f(x) - kx) = b (двусторонняя асимптота), k, lim if(x) - kx) = b (асимптота па +ooj, k, lim (f (x) - kx?j = b (асимптота па - ooj.
ж^ - оо
|

|
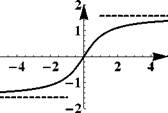
Рис. 5: Примеры горизонтальных асимптот
Замечание 2. Имеет место аналог замечания 1.
Правило: Если функция f является отношением двух многочленов, то следует сначала искать первые пределы. Во всех остальных случаях следует сначала искать вторые и третьи пределы.
Задача 23. Найдите наклонную асимптоту к графику функции
| y |
2x^ + x + 5
x +2
| 2 x 2 + x + 5 lim =2, (x + 2) x x→∞ 2 x 2 + x + 5 |
Решение. Найдем k и b: k = lim f (x)
ж^оо x
| 2 x |
| x +2 |
| 2 x 2 + x + 5 - 2 x 2 - 4 x |
b = lim (f(x) — kx) = lim
= lim
ж^оо x + 2
-3 x + 5
= lim -------------- = —3.
ж^оо x + 2
Ответ: Прямая y = 2x — 3 является двусторонней наклонной асимпто
той. П
-4 ,-| 2 - -
-20
-40
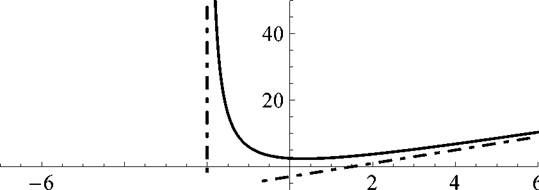
Рис. 6: График функции y
2 x 2 + x +5 x +2
Замечание 3. Горизонтальные асимптоты можно рассматривать как частный случай наклонных асимптот, соответствующий k = 0. Поэтому их также можно находить с помощью теоремы 36.
5.7 Общая схема построения графика
Исследование графика функции рекомендуется проводить в следующей последовательности.
1. Найти ОДЗ.
2. Проверить функцию на четность-нечетность и периодичность.
3. Пайти вертикальные асимптоты.
4. Пайти наклонные (горизонтальные) асимптоты.
5. Вычислить производную. Пайти промежутки возрастания и убывания, а также точки локального экстремума.
6. Вычислить вторую производную. Пайти промежутки выпуклости вверх и вниз, а также точки перегиба.
7. Пайти координаты характерных точек графика (точки экстремума, точки перегиба, точки пересечения с осями).
8. Построить график.
Задача 24. Исследовать график функции
x ^ + x - 1 x ^ + x - 1
y
| (x |
1)2 x 2 - 2 x + 1
Решение. 1. Находим ОДЗ. Единственным препятствием для вычисления аналитического выражения, задающего функцию, может быть обращение в ноль знаменателя. Для нахождения точек, где знаменатель обращается в ноль, регпаем уравнение (x - 1)^ = 0. Очевидно, решением является x = 1. Итак, ОДЗ: x = 1.
2. Правило: чтобы проверить функцию на четность и нечетность, надо выписать f(-x) и f(x) и проверить выполпение равенств f(-x) = f(x) и f(-x) = -f(x).
Вычисляем f(-x) и сравниваем с f(x):
(x)2 x 1 x2 x 1 f (-x)
(-x - 1)2 (x + 1)2
x 2 + x- 1
(x - 1)2
Видим, что ни равенство f(-x) = f (x), ни равенство f(-x) = -f(x) не выполняются. Значит, f не является ни четной, ни нечетной (функция общего вида).
3. В силу правила со с. 57 единственной точкой x о, подозрительной на наличие вертикальной асимптоты, может быть только точка xq = 1. Проверяем (см. правило па с. 58 и теорему 16):
lim f(x) = lim x 2 -------------- = ----------------- ^ = ^ - ^
Вывод: в силу теоремы 35 прямая x = 1 является двустороппей вертикальной асимптотой.
4. Вычисляем пределы па бескопечпости (правило со с. 59 и теоре
ма 17):
k = lim --------- = lim= 0,
ж^оо x х^ж (x 2 - 2 x + 1)x
b = lim f(x) - k • x = lim------------------------- 0 • x = 1.
ж^оо ж^оо x 2 - 2 x + 1
Вывод: в силу теоремы 36 прямая y = 1 является двусторонней наклонной (горизонтальной) асимптотой.
5. Находим ироизводпую:
f (x)
| (x |
1)2
= 1 + 2 x 2(- 1 + x + x2) =
(1-x) + (1 -x)' 3 x - 1 = - (x- 1)з .
Правило: далее находим точки, в которых производная равна нулю или не определена.
Числитель может обращаться в ноль только когда 3 x - 1 = 0, т. е. когда x = 1 / 3. Аналогичным образом знаменатель может обращаться
в ноль только в точке x = 1. Таким образом, действительная ось разбивается на три промежутка, где производная имеет постоянный знак: (—00,1 / 3), (1 / 3,1) и (1,+оо). Взяв но произвольной точке из каждого промежутка, выясняем, что знаки производной в этих промежутках следующие: —, + и — соответственно. Изображаем результат на рис. 7. Выводы: па промежутке (—оо, 1 / 3) функция убывает, па промежутке (1 / 3,1) функция возрастает, на промежутке (1,+оо) функция убывает. Кроме того, при переходе через точку x 0 = 1 / 3 производная меняет знак с минуса па плюс. Значит, точка x 0 = 1 / 3 является точкой минимума.^^

|
Рис. 7: Знаки производной функции y =
(x- 1)2
6. Находим вторую производную:
x 2 + x — 1\" ( 3 x —1\' 6 x
| - 1)2 (x - 1)3 (x - 1)4 |
| (x |
f (x)
Правило: далее находим точки, в которых вторая производная равна нулю или не определена.
Числитель обращается в ноль, когда x = 0. Знаменатель обращается в ПОЛЬ в точке x =1.
Таким образом, действительная ось разбивается па три промежутка, где вторая производная имеет постоянный знак: (—оо,0), (0,1) и (1,+оо). Взяв по произвольной точке из каждого промежутка, выясняем, что знаки производной в этих промежутках следующие: —, + и + соответственно.
Выводы: па промежутке (—оо,0) функция выпукла вверх, па промежутках (0,1) и (1,+оо) функция выпукла вниз. Кроме того, при переходе через точку x 0 = 0 вторая производная меняет знак. Значит, точка x 0 = 0 является точкой перегиба.
7. Правило: чтобы найти точки пересечения графика с осями, надо в уравпепие y = f(x) сначала подставить x = 0 и найти соответствующее y, а затем подставить y = 0 и найти соответствующие x.
^^При переходе через точку x i = 1 функция меняет знак с плюса на минус. Но мы не делаем вывод о наличии в этой точке максимума, поскольку в пей функция пе определена.
| 02+0 - 1 |
| x 2+ x- 1 |
Найдем точку пересечения с осью Y. Вычисляем: f (0) (0 - 1)2 Получилась точка (0 ,- 1).
| √ 1 - |
| 1+v |
| 1,618. |
Найдем точки пересечения с осью X: Составляем уравнение: (-^)2 0 или x 2 + x - 1 = 0. Решая это квадратное уравнение, получае - x1
| (1 / 3)2+1 / 3 - 1 |
0, 618 и x2
Найдем значение функции в точке минимума: f (1 / 3) = (1 / 3 - 1)2 = - 5 / 4. Получилась точка (1 / 3 ,- 5 / 4).
Значение в точке перегиба уже вычислялось: f (0) = - 1.
8. Построим график. Правило: Сначала рисуем асимптоты и отме
чаем характерные точки, см. рис. 8. Затем рисуем график на каждом
из промежутков монотонности, следя за тем, чтобы на границах этих
промежутков функция приближалась к асимптотам, см. рис. 9. П
| i | ^ | |
| -4 -2 -2 | 2 4 6 8 |
Рис. 8: График функции y = j^^rriw'- начало построения Задача 25. Исследовать график функции
-2x
y = xe.
Решение. 1. Находим ОДЗ. Очевидно, функция определена на всей действительной оси.
|
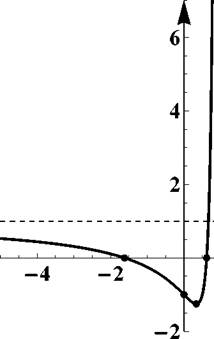
Рис. 9: График функции y = ^(2^ + - 1 - )2 1
2. Исследуем функцию на четность и нечетность. Для этого вычисляем f(—x) и сравниваем с f(x):
| 2 x |
| xe 2 x |
f (-x) = f (x) = xe
Видно, что ни равенство f(—x) = f(x), ни равенство f(—x) = —f(x) не выполняются. Таким образом, функция не является ни четной, ни нечетной (общего вида).
3. Правило. Если функция всюду определена и непрерывна, то вертикальных асимптот пет, см. с. 57.
4. Находим наклонные асимптоты, используя правило со с. 59, прави-
ло Лопиталя (см. пример 22):
('У* e
k = lim f x) = lim = lim e- 2^ =
= {e-^} = 0, b = lim f(x) - kx = lim xe- 2 '^ - 0x = { оо • 0 }
ж^+оо ж^+оо
x г оо ^ x' 1
= lim ^— = < — = lim = lim 2
ж^+оо e схэ ж^+оо (e) ж^+оо 2 e
0,
—
+oo
Вывод: прямая y = 0 является одпостороппей горизонтальной асимптотой на +00.
(
lim f x) = lim xe- 2 = {e +°° } =+00.
ж^ - оо x ж^ - оо x
Вывод: по мере удаления x в - оо функция неограниченно убывает. 5. Находим производную:
| e - 2. |
f(x) = (xe- 2")' = (1 - 2 x)
Находим нули производной:
(1 - 2 x) e- 2^ = 0.
Множитель e- 2^ не обращается в ноль. Поэтому на него можно сократить:
1 - 2 x = 0.
Решая это уравнение, получаем x = 1 / 2.
Таким образом, действительная ось разбивается па два промежутка, где производная имеет постоянный знак: (- оо,1 / 2) и (1 / 2,+оо). Взяв по произвольной точке из каждого промежутка, выясняем, что знаки в этих промежутках следующие: + и - соответственно.
Выводы: на промежутке (- оо, 1 / 2) функция возрастает, а на промежутке (1 / 2, +оо) функция убывает. Кроме того, при переходе через точку x 0 = 1 / 2 функция меняет знак с плюса на минус. Значит, по теореме 31 точка x 0 = 1 / 2 является точкой максимума.
6. Находим вторую производную:
f"(x) = (xe- 2")'' = ((1 - 2 x) e- 2")' = 4(x - 1) e
2 x
| - 2 x |
Рис. 10: Знаки ироизводиой функции y = xe
Находим нули второй ироизводиой:
4(x 1) e
2 x
0.
Множитель 4 e ^^ не обращается в ноль. Поэтому на него можно сократить:
x- 1 = 0.
Решая это уравнение, получаем x = 1.
Таким образом, действительная ось разбивается на два промежутка, где производная вторая имеет постоянный знак: (- оо,1) и (1,+оо). Взяв но произвольной точке из каждого промежутка, выясняем, что знаки в этих промежутках следующие: - и + соответственно.
Выводы: на промежутке (- оо, 1) функция выпукла вверх, а па промежутке (1,+оо) функция выпукла вниз. Кроме того, точка x о = 1 является точкой перегиба.
7. Найдем точку пересечения с осью Y. Вычисляем: f (0) = 0 e- ^'*^ = 0. Получилась точка (0,0).
Найдем точки пересечения с осью X. Составляем уравнение: xe- ^^ = 0 или x = 0. Снова получилась точка (0,0). Таким образом, точка пересечения с осью X и точка пересечения с осью Y — это одна и та же точка.
| 2 e |
Найдем значение функции в точке максимума: f(1/2)
0,1839. Получилась точка (1 / 2; 0,1839).
Найдем значение функции в точке перегиба: f (1) = 1 • e- ^ ~ 0,1353.
8. Построим график, см. рисунок 11. Сначала рисуем асимптоту и
характерные точки. Затем рисуем график па каждом из промежутков
мопотопности. П
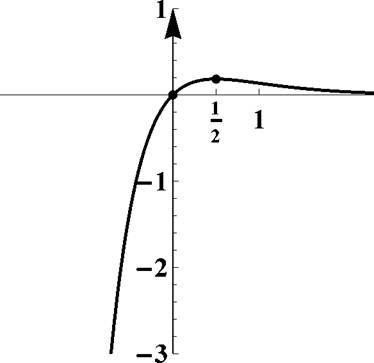
|
Рис. 11: График функции у = хё
2 x
Глава 6
Функции нескольких переменных
6.1 Определение функции нескольких неременных
Функцией двух переменных называют правило, которое каждому упорядоченному набору (x, y) G Ш 2 из двух действительных чисел ставит в соответствие число z G М. Например, S = a • b — площадь прямоугольника, S = v • t^ z = x 2 + y 2. Можно задавать аналитически, таблично, графически.
Обозначения: z = f(x,y) или z = f (x ¯), где x ¯ = (x,y) или x ¯ = (x 1 ,x 2).
Аналогично определяют функцию n переменных.
| состоящее из |
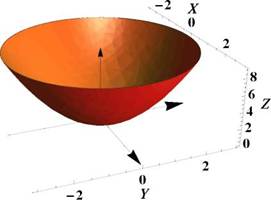
График функции z = f(x,y) — это подмножество точек, имеющих координаты вида (x,y,f (x,y)).
|
Линией уровня функции z = f(x,y)^ соответствующей значению C G М, называют множество точек на плоскости, являющихся решениями уравнения
Линию уровня можно получить, спроектировав па плоскость XY пересечение графика функции с горизонтальной плоскостью z = C. Примеры: географическая карта, линии равных температур.
Для функции трех перемеппых аналогом линии уровня являются поверхности уровня.
Пусть x иy означают объем товаров (услуг), способные заменять друг друга (хлеб и колбаса, театр и футбол). Пусть z = f(x,y) — полезность (калории, % восстаповлеппой работоспособности) от потребления объемов товаров x и y. Линии уровня этой функции {функции полезности) называют кривыми безразличия.
Частной производной функции z = f(x,y) но переменной x называют обычную производную функции z = f(x,y) по переменной x, посчитанную в нредноложении, что y является константой. Аналогично определяют частную производную функции z = f(x,y) по переменной y и частные производные функций больгпего числа неременных. Частную производную функции z = f(x,y) но неременной x обозначают симво-
X И ai ИЛИ z ^ И ^.
Задача 26. Вычислить z^ и z'y для функции z = x'^y^. Решение. Имеем
(xy) y = x (y) y = x^5y^ = 5x-y. □
Градиентном или полной производной функции многих переменных называют вектор, составленный из частных производных:
g ra df(x,y) = f(x,y) = {f^(x,y), fy(x,y)) =
∂f () ∂f
Геометрический смысл градиента: градиент перпендикулярен линиям (поверхностям) уровня и направлен в сторону возрастания функции; его длина равна скорости возрастания функции в данном направлении.
Полная производная позволяет приближепно вычислять приращепие функции. А именно. Положим
∆ f = f(x + ∆x,y + ∆ y) - f(x, y).
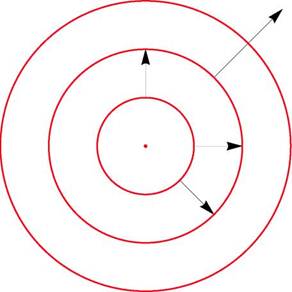
|
Рис. 3: Градиент функции z = x^ + y^
Тогда
∆ f «(f (x,y),∆ x ¯) =
где
∆ x ¯ = (∆ x, ∆ y) .
6.3 Частные производные выснгих порядков
Частной производной второго порядка называют частную производную от первой частной производной. Обозначения для z = f(x,y):
∂x∂x
∂y∂x
∂x∂y
∂y∂y
Различают чистые (все время по одной переменной) и смешанные частные производные (по разным переменным) высших порядков.
У функции n переменных производных 1-го порядка n штук, 2-го — n ^ штук и т.д.
Теорема 37. Если смешанные частные производные непрерывны, то они не зависят от порядка дифференцпровання.
Матрицей Гессе функции f называют матрицу, составленную из всевозможных частных производных 2-го порядка. Для функции z = f(x,y) она выглядит так
fxу(x,y) fу 2(x,y)
Для функции n переменных
f
dx2dx1
9 x 19 x 2 dx 22
dx1dxn дx 2 дxn
dxndx1 дxnдx2
dx 2 n
6.4 Экстремум функции нескольких переменных и его необходимое условие
Пусть z = f(x,y) — функция двух переменных.
Точку (x о ,y о) называют точкой (нестрогого локального) максимума функции f, если для всех x, близких к x о, и для всех y, близких к y о, выполняется неравенство f (x,y) < f (x о ,y о)-
Точку (x о ,y о) называют точкой (нестрогого локального) минимума функции f, если для всех x, близких к x о, и для всех y, близких к y о, выполняются неравенство f (x,y) > f (x о ,y о)- Слова "нестрогий" и "локальный" обычно опускают.
Для максимума и минимума функции используют общее название экс-нпремум. Значения функции в точках экстремума называются соответственно максимумом и минимумом функции.
Теорема 38 (необходимое условие экстремума). Пусть функция z = f (x,y) определена всюду н всюду имеет частные производные. Для того чтобы функция z = f(x,y) имела локальный экстремум в точке (x о, y о); необходимо, чтобы выполнялось условие
fx (x о ,y о) = 0, f (x о ,y о) = 0 .
(6.1;
Точки, в которых выполнено условие (6.1), называют критмческими.
Задача 27. Найти
z = 4x + 3y + x^ — xy — y^
критические
точки
функции
Решение. Вычислим частные производные:
z^
(4 x + 3 y + x 2 - xy - y2)\. = 4 + 0 + 2 x-y- 0
z!у = (4x + 3y + x2-xy- y2) у = 0 + 3 + 0-x-2y.
Приравняем их к нулю:
4 + 2 x-y = 0, 3-x-2y = 0.
Решая эту систему, получаем, что x = - 1, y = 2.
6.5 Достаточное условие экстремума функции нескольких неременных
Теорема 39. Пусть функция z = f(x,y) всюду имеет непрерывные частные производные 2-го порядка. Если в критической точке (x 0, y 0) матрица Гессе является
♥ полоясительно определенной, то (x 0 ,y 0) ^ точка локального минимума;
♥ отрицательно определенной, то (x 0 ,y 0) ^ точка локального максимума;
♥ знакопеременной, то в (x 0 ,y 0) экстремума нет.
Теорема 40 (критерий Сильвестра). Матрица
/a 11 a 12 a 13
A= a 21 a 22 a 23 a 31 a 32 a 33
полоясптельно определена тогда и тогда, когда ∆1 > 0, ∆2 > 0, ∆3 > 0,
где
| a 11 a 12 a 21 a 22 |
| ∆ |
| ∆ |
a 11 a 12 a 13
| a 21 a 22 a 23. a 31 a 32 a 33 Матрица A отрицательно определена тогда и тогда, когда ∆1 < 0,∆2 > 0, ∆3 < 0. |
∆1 = a 11,
Глава 7
Неопределенный интеграл
7.1 Определение первообразной и неопределенного интеграла
Функцию F называют первообразной функции f, если
F'(x) = f(x).
Таким образом, нахождение первообразной есть действие обратное нахождению производной.
Пример 28. Первообразной функции f (x) = x является функция F q(x) = Y- Действительно, Fq(x) = (у) = x. Но функция F i(x) = у + 3 также является первообразной функции f(x) = x.
И вообще, при любом значении константы C G М функция F(x) = у + C является первообразной функции f(x) = x.
Этот пример показывает, что первообразных может быть много. Оказывается, это — общая ситуация. Она описывается в следующей теореме.
Теорема 41. Пусть область определения функции f представляет собой промежуток (интервал, отрезок, полуинтервал, полуось или всю ось). Если известна хотя бы одна первообразная F функции f, то множество всех ее первообразных описывается формулой
F(x) + C,
где C пробегает миоукество всех действительных чисел.
Неопределенным интегралом от функции f называют множество всех ее первообразных. Неопределенный интеграл от f обозначают символом J f(x) dx. В силу теоремы 41
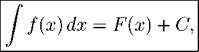
где F — какая-нибудь первообразная, а C пробегает множество всех действительных чисел.
Еще раз подчеркнем, что в отличие от первообразной неопределенный интеграл является не функцией, а семейством функций.
Часть f(x) dx обозначения J f(x) dx называют поды,нтегральны,м выражением^ а функцию f, от которой берут интеграл, — подынтегральной функцией.
Как правило, на символ / в обозначении интеграла удобно смотреть как на открывающуюся скобку, а на символ dx — как на закрывающуюся; то, что находится между ними, надо проинтегрировать.
Иногда бывает полезно буквальное понимание символа J f(x) dx. В нем часть f(x) dx представляет собой дифференциал неизвестной функции F. Нахождение первообразной (неопределенного интеграла) есть восстановление функции F но ее дифференциалу.
По интуитивному смыслу dx есть бесконечно малое число, а f(x) — его коэффициент. В этом контексте символ / (представляющий собой вытянутую латинскую букву S — начальную букву слова "суммировать") означает суммирование бесконечно большого числа бесконечно малых величин f(x) dx. Поскольку dx можно интерпретировать как множитель, его часто с целью экономии места пишут не в конце, а например, в числителе: Г—.
 2014-02-24
2014-02-24 594
594








