X^a
X-^2
X^a
Ik
2)0
3-2-1 12 3
A x
Рис. 5: \x — a\ есть расстояние от x до a
a-е a a+е
Рис. 6: ε -окрестность точки a — иромеясуток a — ε<x<a + ε
Множество всех x, удовлетворяющих неравенству \x\ > N, называют N-окрестностью точки оо.
Теорема 4 (неравенство треугольника). Для любых чисел x и y
\x + y\ < \x\ + \y\.
1.4 Функции и способы их задания
Пусть X hY множества. Функцией называют правило, но которому каждому x G X ставится в соответствие y ^Y. Множество X называют .мноэюесшвсм определения функции, а Y — мноэюесшвом значений. Если X и Y являются подмножествами М, то функции называют числовыми.
-N0N
Рис. 7: N -окрестность точки оо
х + у
х+у
Рис. 8: Неравенство треугольника
Чтобы о функции можно было говорить коротко, функции дают имя. Например, ln, exp, sin. Это — имена стандартных функций. В качестве имени функции, с которой работают временно, обычно используют букву f. Символ f(x) означает значение функции в точке x, т. е. тот y, который сопоставляется функцией данному x. Подчеркнем, что символы f и f(x) имеют разный смысл, f есть имя функции, а f(x) — число. Иногда для большей выразительности речи символы f и f(x) пе различают. Если имя функции не было задано, то но умолчанию используют обозначения
yиy(x).
Для некоторых часто встречающихся ситуаций имеются общепринятые символические сокращения. Например, тот факт, что f есть функция с областью определения X и множеством значений Y символически записывают так:
f:X^Y
и коротко читают так: f действует из X bY. Но аналогии с этим вместо y = f(x) можно написать
f: x^y,
что коротко читают так: f переводит x в y. Способы задания функции:
(а) Аналитический способ: указывается формула, по которой, зная x, можно вычислить y. Например, y = x^ или y = л/x. Областью определения функции, заданной аналитически, по умолчанию считают множество всех x, для которых аналитическое выражение имеет смысл {область допустимых значений или ОДЗ). Иногда функцию задают с помощью нескольких аналитических выражений, соединенных логическими операциями; примером такого задания является формула (1.1).
(b) Табличный способ: перечисляют все x G X и для каждого из них указывают соответствующий y ^Y. Например,
| x | |||
| y | 0,7 | 0,24 | 0,06 |
Недостаток этого способа заключается в том, что с его иомогцью можно задать только функцию, имеюгцую конечную область определения.
(с) Графический способ: задается график функции. Графиком функции f называют множество точек на плоскости, имеюгцих координаты (x, f(x)). Примеры: рис. 13 и 14. Преимущество графического способа задания — его наглядность, а недостаток — невысокая точность.
|
Рис. 9: График функции y
x
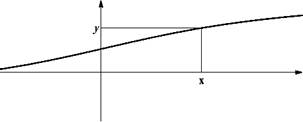
Чтобы но графику, зпая x, вычислить f (x), надо пайти на оси X точку x, восстановить из нее нернендикуляр до пересечения с графиком, а затем через точку пересечения провести горизонтальную прямую; эта горизонтальная прямая пересечет ось Y как раз в точке
y = f(x).
Универсальный, по медленный способ построение графика:
надо нарисовать много точек с координатами (x,f (x)) и соединить их плавной линией.
(d) Неявный способ: зависимость y от x задается уравиеиием F(x,y) 0. Например, x 2 + y 2 = 1.
2 /
1 /
-----,------,---- /_ --,-----,--- ^.
3 -2 - 1 12 3
/ -2
^ -3
\ 2 /
\ 1 /
------------------------------- Jb.^-d£----------------------------- ^.
-1
-2
-3
t /
2 /
1 /
------------,—------ Z. —,---------- ^.
3 -2 - 1 12 3
/- 1
-2 ' -3
|
| Рис. 10: Графики функций слева направо: y = x, y = x"^, y = x^ |
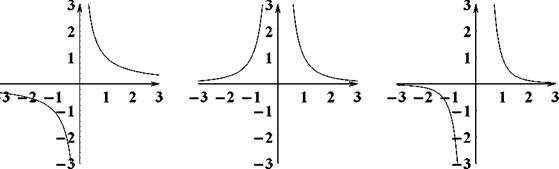
Рис. 11: Графики функций слева направо: y = 1/x, y = 1 /x ^, y = 1/x^
1.5 Обратная функция
Обратной по отношению к функции f: X ^ Y называют функцию f ~1: Y ^ X, которая но y восстанавливает x. Иными словами: для любого x G X из f(x) = y следует f~ 1 (y) = x.
Чтобы но y можно было восстановить x, необходимо, чтобы разные x переходили в разные y, т. е. их x1 = x 2 следует f(x1) = f (x 2).
Чтобы f ~1: Y ^ X была определена на всем Y, необходимо, чтобы в каждый y ^ Y переходил хотя бы один x G X, т. е. чтобы образ f совпадал с Y.
Правило: графики прямой и обратной функций симметричны относительно прямой y = x.
И
| 1.5 | 1.5 | 1.5 | |||||||||||||||
| 0.5 | 0.5 | 0.5 | |||||||||||||||
| -2 | -1 0.5 -1 -1.5 -2 | -3 | -2 | -1 0.5 -1.5 -2 | -3 | -2 | -1 0.5 -1.5 -2 |
Рис. 12: Слева: график функции y = -\/ x, в центре: график функции y = -у x; справа: те ясе графики в единых осях координат
|
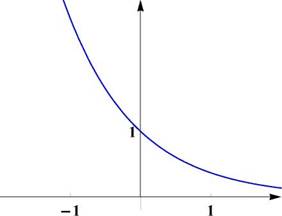
|
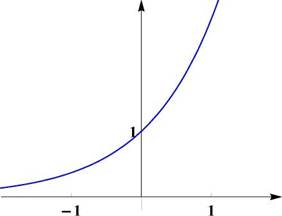
Рис. 13: Графики показательных функций. Слева: y = ax (0 < a < 1). Справа: y = ax (0 < a < 1) или y = a~x {a > 1)
(a > 1) или y
Функция y = x^ обладает обоими дефектами: точки x и —x она склеивает, т. е. переводит в один и тот же y] а ее образ не совпадает с М. Поэтому чтобы определить обратную функцию, множество значений сужают до [0,+оо), а область определения — до неотрицательных x. Получающуюся обратную функцию называют арифметическим корнем,.
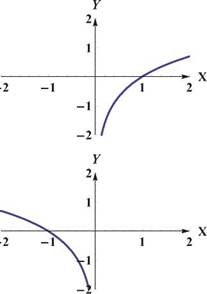
|
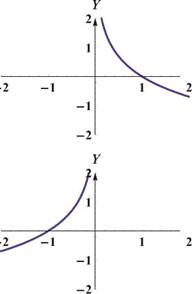
|
| *- X |
| *^ X |
Рис. 14: Графики логарифмических функций. Первая строка: график функции y = log ax, слева a > 1, справа 0 < a < 1. Вторая строка: график функции y = log a (— x), слева a > 1, справа 0 < a < 1.




Рис. 15: Графики функций y = s in x, y = cos x, y = — s in x, y = — cos x,
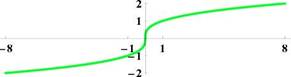

|
|
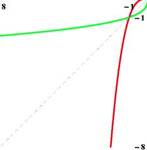
Рис. 16: Слева: график функции у = х^, справа: график функции у = \[х
Рис. 17: Графики функций у = х^ и у = \[х

|
-2-1 1 2
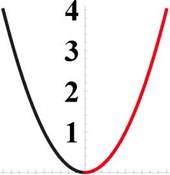
Рис. 18: Слева: график функции у = х"^, справа: график функции у = л/х
4 г;
\ 3 /
\ 2 / ^^^^
2 -1 12 3 4
^/'' -1-
-2
Рис. 19: Графики функций у = х^ я у = \/х
|
|
| -3 -2 -1 |
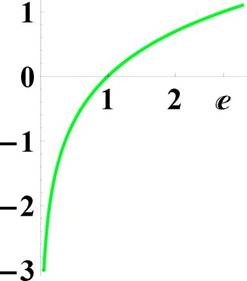
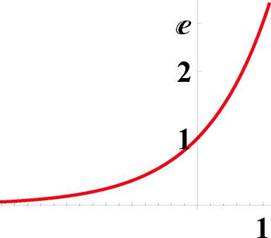
Рис. 20: Слева: график функции у = ex, справа: график функции у = 1пх
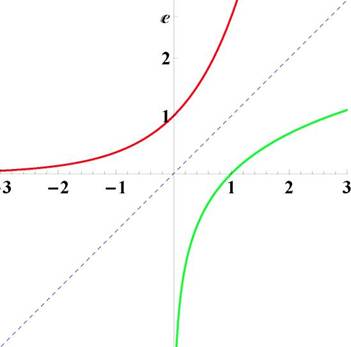
Рис. 21: Графики функций у = ex я у = 1пх
Рис. 22: График функции y = s in x
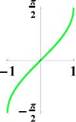
Рис. 23: График функции y = arcsin x
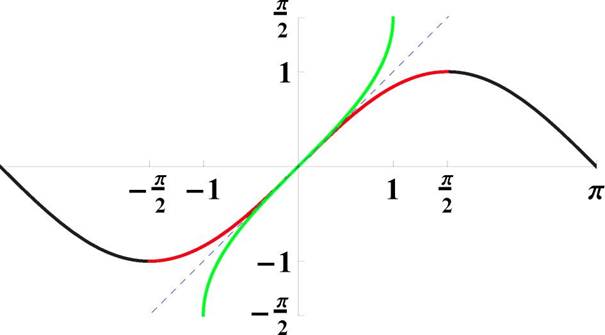
Рис. 24: Графики функций y = sinx я y = arcsin x
Рис. 25: График функции у = cos ж
л
-1
Рис. 26: График функции у = arccos х
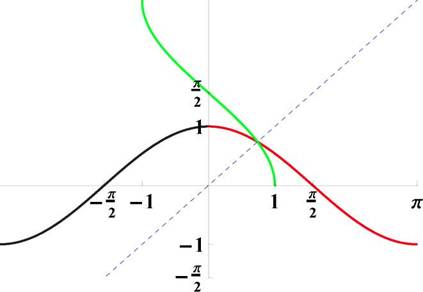
Рис. 27: Графики функций у = cos ж и у = arccos ж
1.6 Элементарные свойства функций
Функцию называют четной^ если f(—x) = f(x). Пример: y = xn, где n — четное. График четной функции симметричен относительно оси Y. См. рис. 10, 15.
Функцию называют нечетной, если f(—x) = —f(x). Пример: y = xn, где n — нечетное. График нечетной функции симметричен относительно начала координат. См. рис. 10, 15, 23, 28, 29, 31.
Правило: чтобы проверить функцию на четность и нечетность, надо вычислить f (—x) и f(x) и сравнить их.
Говорят, что функция f имеет период T, если
f(x + T) = f(x).
Функцию f называют ограниченной, если |f (x) | < C для всех x, где C не зависит от x. График ограниченной функции содержится в полосе
|y| < C.
См. рис. 15, 28, 31.
1.7 Слож:ная функция
Слоэюной функцией называют функцию вида y = f(u(x)). Говорят также, что это суперпозиция или композиция, функций f и u. Функцию f называют внешней, а функцию u — внутренней.
Пример 1. Функция y = l n x является сложной с внутренней u (x) = ln x и внешней f(u) = u^.
1.8 Элементарные функции
Основными элементарными функциями называют функции следующих пяти классов:
(a) y = xα — степенная;
(b) y = ax — показательная, здесь a > 0;
(c) y = log a x — логарифмическая, здесь a > 0,a = 1;
(d) y = sin x и y = cos x — тригонометрические;
(e) обратные тригонометрические.
Графики основных элементарных функций надо знать наизусть.
Элементарной называют функцию, заданную с помощью (одного) аналитического выражения, составленного из констант, основных элементарных функций, знаков арифметических действий и операции образования сложной функции.
Пример 2. Функция у = \х\ не является элементарной.
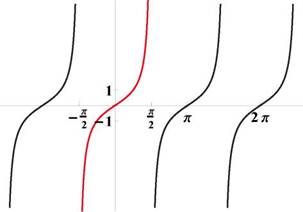
Рис. 28: График функции y = tgx
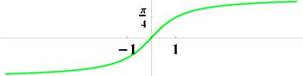
Рис. 29: График функции y = arctg x
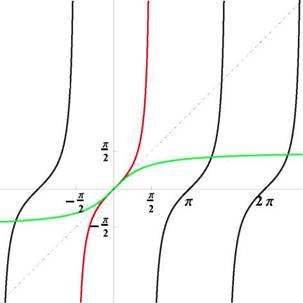
Рис. 30: Графики функций y = tgx и y = arctg x
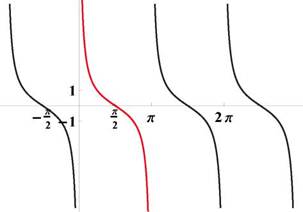
Рис. 31: График функции y = ctg x
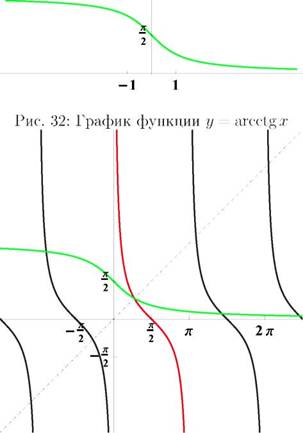
Рис. 33: Графики функций y = ctg x и y = arcctg x
Глава 2
Уравнение прямой
2.1 Уравнение линии на плоскости
С интуитивной точки зрения линия — это след, оставляемый движущейся точкой.
Уравнением линии называют уравнение, которому удовлетворяют координаты каждой точки, принадлежащей данной линии, но не удовлетворяют координаты любой точки, не принадлежащей данной линии. Например, y = x^, x^ +y^ = 1.
Правило: Чтобы проверить, принадлежит ли точка линии, надо координаты точки подставить в уравнение линии.
Различают два тина уравнений:
y = f (x), (2.1)
F(x,y) = 0. (2.2)
Примеры таких уравнений:
x^ + y^ = 1.
В уравнении (2.1) неизвестная y явно выражена через x. Такой способ задания называют явным. Чтобы, зная x, с помощью уравнения (2.2) найти y, надо это уравнение решить. Такой способ задания называют неявным.
Правило: чтобы найти точку (точки) пересечения двух линий, надо выписать систему, состоящую из уравнений этих линий, и решить ее.-^^
^^Часто это правило формулирует не виолне корректно: надо приравнять y. Это путь можно реализовать только при условии, что оба уравнения являются явными.
2.2 Уравнение прямой с угловым коэффициентом
Уравнением прямой с угловым коэффициентом, называют уравнение вида
y = kx + b.
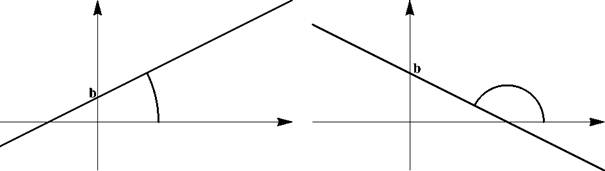
В нем коэффициент k имеет геометрический смысл тангенса угла между осью X и прямой.^^ Число k называют угловым коэффициентом прямой. Если k > 0, то график прямой возрастает. А если k < 0, то график прямой убывает. Число b имеет геометрический смысл координаты точки пересечения прямой с осью Y.
|
Рис. 1: Слева: k > 0; справа k < 0
Правило: Угловой коэффициент — это то, на что умножается x в явном, уравнении прямой. Примеры: 2y + 4 x = 6 и y = — 2 x + 3.
Задача 1. Составьте уравнение прямой, проходящей через заданную точку (x о ,y о) с заданным угловым коэффициентом k.
Решение. Ответом является уравнение
y - y 0 = k (x - x 0).
Эту формулу надо знать наизусть.
2.3 Общее уравнение прямой
Не все прямые можно задать уравнением с угловым коэффициентом. А именно, исключепием является вертикальная прямая (см. рис. 2):
x
a.
тсчитываемого в направлении от оси к прямой.
Общим уравнением прямой называют уравнение
Ax + By + C = 0
в предположении, что хотя бы одно из чисел A, B не равно нулю. Это уравнение охватывает все тины прямых.
Рис. 2: Вертикальная прямая
2.4 Уравнение прямой,
проходящей через две заданные точки
Задача 2. Составьте уравнение прямой, проходящей через две заданные точки (x о ,y о) и (xi,yi).
Решение. Ответом является уравнение
| y -y 0 |
x-x 0
y 1 -y 0 x 1 -x 0
Универсальный способ построения прямых: надо нарисовать две точки, лежащие па прямой, и провести через них прямую.
2.5 Условие параллельности
и перпендикулярности прямых
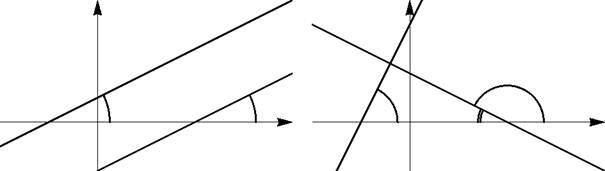
Теорема 5. Пусть даны две прямые y = k1x + b1 иy = k 2 x + b 2- Для того чтобы эти прямые были параллельны, необходимо и достаточно, чтобы
k 1 = k 2.
Для того чтобы прямые были перпендикулярны, необходимо и достаточно, чтобы
k 1 k 2
1.
|
Рис. 3: Идея доказательства теоремы 5
Задача 3. Дана прямая 2y+3x-7 = 0. Составьте уравнения двух прямых, проходящих через точку (5,9), одна из которых параллельна, а другая — перпендикулярна исходной.
Решение. Выясним, какой угловой коэффициент у исходной прямой:
(Угловой коэффициент — это то, на что умножается x в явном, уравнении
прямой.)
3 7 k 3
y 22 2
Выпишем уравнение параллельной прямой (используя задачу 1: y -y 0 = k(x -x 0 )):
| (x |
| 5). |
y - 9
Выиигпем уравнение перпендикулярной прямой (используя условие перпендикулярности k1k2 = - 1):
y- 9 = -(x- 5).
П
Глава 3
Пределы и непрерывность
3.1 Определение числовой последовательности
Числовой последовательностью или просто последовательностью называют правило, по которому каждому натуральному числу п ставится в соответствие действительное число Хп- Таким образом, последовательность — это функция, областью определения которой является множество N натуральных чисел.
Последовательность можно задавать аналит,ически: Хп = п2, или пу
тем перечисления членов (этот способ апалогичеи табличному заданию
функции): Xi = 12, Х2 = 22, жз = 32,____
Пример 3.
| 12345 1, 1,1, 1, |
| - 1, 1, - 1, 1, 2, 22, 23, 24, |
| равносильно | xn =, |
| равносильно | xn = (- 1) n +1, |
| равносильно | xn = (- 1) n, |
| равносильно | xn =2 n. |
Интуитивно последовательность моделирует движение в дискретном времени.
3.2 Определение предела последовательности
Говорят, что число в является пределом последовательности Хп-, если чем больше становится п, тем меньше Хп отличается от В. Символически это записывают так:
lim Хп = В.
Интуитивно определение предела означает следующее: с ростом n числа ближе и ближе подходят к B.
Пример 4. lim - = 0, последовательность xп = (—1)"^ не имеет предела,
п^оо
lim 2" = +00.
Бесконечности (оо, ± оо) — значки, пе имеющие точного буквального смысла. Имеется три символа бесконечности: +оо находится правее всех действительных чисел, а — оо — левее; оо (бесконечность без знака) представляет собой склеенные вместе +оо и — оо (очень длинную прямую прикладывают к экватору и изгибают). В речи символы бесконечности используются только в конструкциях типа "движение в сторону бесконечности". См. рис. 7.
3.3 Предел функции на бесконечности и в точке
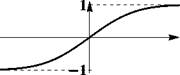
(a) Говорят, что предел f(x) при x, стремящемся к +оо, равен B и
пишут
lim f(x) = B,
если чем больше становится x, тем меньше f(x) отличается от B.
(b) Говорят, что предел f(x) при x, стремящемся к —оо, равен B и
пишут
lim f(x) = B,
если чем меньше становится x, тем меньше f(x) отличается от B.
(c) Говорят, что предел f(x) при x, стремящемся к оо, равен B и пишут
lim f(x) = B,
если чем больше становится |x|, тем меньше f(x) отличается от B.
|
|
Рис. 1: Пределы функции на бесконечности
(c) Говорят, что предел f(x) при x, стремящемся к a, равен B и пишут
Ит f(x) = B,
если чем ближе x подходит к a, тем меньше f(x) отличается от B.
(d) Говорят, что предел f(x) при x, стремящемся к a справа, равен B и
пишут
Ит f (x) = B,
x^a+0
если чем ближе x подходит к a справа, тем меньше f(x) отличается от B.
Аналогично определяется предел слева
Ит f(x) = B.
См. рис. 3.
(e) Говорят, что предел f(x) при x, стремящемся к a, равен оо и пишут
Ит f(x) = оо,
x^a
если чем ближе x подходит к a, тем меньше f(x) отличается от оо. Аналогично определяется
Ит f(x) = ± 00 .
x^a
См. рис. 11 и 14. Задача 4. Проверить, что (см. графики на рис. 13, 14)
Ит - = О, И+ ex = +оо, Ит ex = О,
x
Ит— не сущ., Ит 1п x = +оо, Ит 1п x = —оо.
x^ 0 \x\ x ^+оо x ^0+0
Теорема 6. Для того чтобы двусторонний предел
Ит f(x)
x^a
равнялся B, необходимо и достаточно, чтобы оба односторонних предела
Ит f(x) и Ит f(x)
x^a— 0 x ^ a +0
равнялись B.
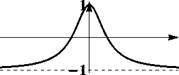
| \х\ |
Рис. 2: График функции y = f-
3.4 Основные теоремы о пределах
Соглашение: в выражении x ^ a иод a обычно будем понимать любой из символов оо, +00, —оо, само a, a + 0 или a — 0.
Теорема 7. Предел константы есть эта константа:
lim C = C.
Теорема 8. Функция не моукет иметь болыие одного предела.
Рис. 3: Графики разрывных функций. См также рис. 2
Теорема 9 (о пределе арифм. операций). Пусть пределы limf(x) и lim g(x) являются числами. Тогда
(a) lim(f (x) ± g(x)) = lim f(x) ± lim g(x);
(b) lim f (x) X g(x) = lim f (x) х lim g(x).
Частный случай: lim C х f (x) = C х lim f (x), где C — константа.
(c) lim = x Г^ a при условии lim g (x) = 0.
| a g (x) |
lim g (x)
Теорема 10 (о пределе сложной функции). Пусть
lim u (x) = b
И
lim f (u) = f(b).
Тоща
limf(u(x)) = f(b).
3.5 Непрерывные функции
Функцию f называют непрерывной в точке a, если предел функции в этой точке равен значению функции в этой точке:
lim f (x) = f (a).
Функцию называют непрерывной^ если она ненрерывна в каждой точке a своей области определения. Геометрически непрерывность функции означает, что ее график — это непрерывная кривая.
Если функция не является непрерывной, то ее называют разрывной^ а точку, в которой непрерывность не имеет места, — точкой разрыва. См. рис. 3.
Следствие 11. Непрерывную функцию моукно выносить за знак предела:
lim f (u (x)) = f (lim u (x)).
Теорема 12. Сумма, разность, нронзведенне и частное [на естественной области онределения) непрерывных функций — иепрерывпая функция. Слоясная функция, составленная из непрерывных функций — непрерывная функция.
Теорема 13. Все основные элементарные функции непрерывны.
Теорема 14. Все элементарные функции непрерывны.
Пример 5.
lim ex = e 4.
3.6 Бесконечно малые функции и их свойства
Говорят, что функция y = α(x) является бесконечно.малой (сокращенно б. м.) при x ^ a, если
lim α(x) = 0. Пример 6. ^ — б. м. при x ^ оо; x ^ — б. м. при x ^ 0; ex — б. м. при
x.
Теорема 15. Для того чтобы lim f(x) = B, необходимо и достаточно, чтобы f(x) = B + α(x) при x ^ a, где y = α(x) — б. м. при x ^ a.
Пример 7. lim x ^оо ^ = lim x ^оо(1 + ^) = 1. Свойства бесконечно малых функций:
(a) Сумма двух или конечного числа бесконечно малых функций есть бесконечно малая функция.
(b) Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция. Частные случаи: ироизведе-ние бесконечно малой функции на функцию, имеющую конечный предел, есть бесконечно малая функция; если бесконечно малую функцию разделить на функцию, имеющую ненулевой предел, то получится бесконечно малая функция.
3.7 Бесконечно больнгие функции и их свойства
Говорят, что функция y = ω(x) является бесконечно большой (сокращенно б. б.) при x ^ a, если
li mω(x) = ОО .
Пример 8. - — б. б. при x ^ 0; x ^ — б. б. при x ^ оо; ln x — б. б. при
x -^ +0; ln x — б. б. при x -^ +оо; ex — б. б. при x -^ +оо; e ~ x — б. б. при x -^ —ОО.
Свойства бесконечно больы1их функций:
(a) Произведение бесконечно большой функции на функцию, имеющую ненулевой предел, есть бесконечно большая функция. Частный случай: произведение двух бесконечно больших функций есть бесконечно большая функция.
(b) Сумма бесконечно большой функции и ограниченной функции есть бесконечно большая функция. В частности, сумма бесконечно большой функции и функции, имеющей конечный предел, есть бесконечно большая функция.
(c) Сумма двух или конечного числа бесконечно больших функций одного знака есть бесконечно большая функция.
Теорема 16. Для того чтобы функция у = а{х) была бесконечно малой, необходимо н достаточно, чтобы функция у = —г^ была бесконечно большой. Для того чтобы функция у = и{х) была бесконечно больгной, необходимо и достаточно, чтобы функция у = ^jt^ была бесконечно малой.
Пример 9. В силу теоремы 14 Ит х"^ = 0. Поэтому но теореме 16 Ит \ =
оо.
Приняты условные обозначения: { 0 } для бесконечно малой функции, { оо } — для бесконечно большой функции и {С} — для функции, имеющей предел С. В этих обозначениях теорему 16 можно записать так:
а свойства бесконечно больших функций — так:
{ С-оо } = { оо }, С=0,
{ оо • оо } = { оо }, { оо + С} = { оо },
{ +оо } + { +оо } = { +оо }.
3.8 Раскрытие неопределенностей
Правило: При вычислении пределов всегда начинают с подстановки в функцию предельного значения. Если получится число, то в силу теоремы 14 оно и является пределом. Если результат подстановки удастся интерпретировать как свойства бесконечно малых и бесконечно больших функций, то также сразу получится ответ.
Пример 10.
x ^оо x
- = 1 = 1 = -
+ 1 oooo + 1 oo + 1 oo
Если же результат подстановки в функцию предельного значения не удается интерпретировать как свойства бесконечно больших и бесконечно малых функций, то говорят, что возникла неопределенность. Примеры: { ^ }, { ^ }, { 0 • оо }, { оо - оо }, { 1°° }, { 0*^ }, { оо*^ }. Вычисление таких пределов называют раскрытием, неопределенностей.
Многочленом называют функцию вида
p (x) = a{)xn + a1xn- 1 + • • • + an
где a о, a 1, •••, an ^ заданные числа. Степенью многочлена называют наибольшую степень x, входягцую в многочлен. Например,
Ф p (x) = 2x2 - 3 x + 5 — многочлен степени 2;
Ф p (x) = 7 x - 1 — многочлен степепи 1;
Ф p (x) = 2 — многочлен степепи 0;
Ф p (n) = n^ + 3 n 2 - n — многочлен от переменной n.
Задача 5. Найти предел
| . 0 |
x 2 - 3 x + 2 г 0
lim
x-^2 x-^ - 5x2 + 6x
Решение. Нетрудно проверить, что при x, стремягцемся к 2, числитель и знаменатель этой дроби стремятся к нулю. Это означает, что x = 2 является корнем многочленов, стоягцих в числителе и знаменателе, поэтому и в числителе и в знаменателе можно выделить множитель (x - 2), а затем его сократить:
x 2 - 3 x + 2 (x-2)(x-1) x-1
x ^ - 5 x 2 + 6 x x(x - 2)(x - 3 ) x(x - 3 )
Теперь при x, стремящемся к 2, числитель стремится к 1, а знаменатель — к - 2. Поэтому предел равен - 1 / 2. Таким образом,
| lim x^2 x |
| x 2 3 x + 2 | x | ||
| — | |||
| x-^ - 5 x 2 + 6x | x-^2 x(x | - 3) |
Сформулируем общее правило: Если предел отношения двух многочленов (в конечной точке) представляет собой неопределенность { 0 }, то числитель и знаменатель имеют общий множитель, на который можно со-
| кратить. | ||
| Пример 11. | ||
| lim 2 | ||
| i- im 1+ |
П
1.
Правило: чтобы посчитать предел отношения многочленов при x -^ оо (представляющий собой неоиределенность {^}), надо в числителе и знаменателе вынести за скобку x в старшей степени, а затем старшие степени сократить.
Теорема 17 (предел рациональной функции).
| 0, | если n <m |
| a | если n = m |
| оо, | если n > m |
lim------------ -------------- = a ^, если n = m (a 0, b 0 = 0),
Правило: предел отношения многочленов при x ^ оо равен: 1) отношению коэффициентов при старишх степенях, если степень числителя равна степени знаменателя; 2) нулю, если степень числителя меньше степени знаменателя; 3) бесконечности, если степень числителя больше степени знаменателя.
| {-} . оо |
x 4 + 3 x + 1
lim ------------------------ = 0,
ж^оо 3x 5 + 8x 2 + 6
ж^оо 4 x 2 + 3x
8 x 3 + 4 x- 5 8
lim
х^оо - 4 x 3 + 2 x 2 + 10
Задача б. Найти предел
| а^^+оо v^ |
2 x 2 + 6 x - 1 lim
Решение. Вынесем за скобку x 3 и сократим. Учитывая, что x 3 = л/ x 9
и x3 = x 6, получим
2 x 2 + 6 x - 1 x 3(2 /x + 6 /x 2 - 1 /x 3
lim --------------------------- = lim
2 /x + 6 /x 2 - 1 /x 3 0 + 0 - 0 0
= lim —, ------ , =---------------------- т= = - = 0. П
^-+°° ^1 - 1 /x 8 + 6 /x 9 + v^1 /x 5 л/1 - 0 + 0 + л/ 0 1
Пример 13.
lim (x - v x 2 + x) = оо - оо
ж^+оо
(x - лx2 + x)(x + лx2 + x )
lim------------------------------- -1 ---------------------------- =
х^+оо (x + лx 2 + x)
lim ------------- ^ = — > = lim ------------------------- ■^^
х^+оо x + л - x 2 + x OO ^^+оО x /'1+ /1 + 1
| (1+1+ 1) |
lim ^ = -.
Правило: чтобы раскрыть неопределенность, созданную разностью корней, стоит нонробовать умножить и разделить на сопряженное выражение.
Сопряженным к выражению лa - уb называют выражение л a + Основное свойство:
(л a - л b)(\ a + уb) = a - b.
(л/ a - v b)(V a 2 + л ab + л b 2) = a - b.
Задача 7. Найти предел
x - 3
lim-------- ,
а^^3 4 - л x +13
| x - 3 =r0l= (x - 3)(4 + л |
Решение.
lim----- = - = lim
| x |
(x - 3)(4 + л x +13) (x - 3)(4 + л x +13)
lim------------------------------ = lim------------------------------ =
х^3 16 - (x + 13) х^3 3 - x
= lim(- 4 - л x + 13) = - 4 - л/3 + 13 = - 4 - 4 = - 8. П
ж^3
3.9 Первый замечательный предел
 2014-02-24
2014-02-24 645
645








