Хо хх хг хъ

Zj Zj

0.5 1.0 1.5 2.0

6 4 2 0

0.5 1.0 1.5 2.0

0.5 1.0 1.5 2.0

Oo

ЛД)

B b b

A a

Jb a

A b

Таблица дифференциалов

α +1

x^α dx

1 ₂ xdx = dx, 2

dx = 2 d√x,

x

e^x dx = de^x

dxα +¹, α= - 1 ,

dx x x ² dx

dx

= x ²

a^x dx

d ln x

d

dx ³

x

1 _x da, ln a

sin x dx dx = cos2 x dx

x

^

= -d cos x, d tg x,

= d arcsin x,

cos xdx = d sin x,

dx

sin2 x

dx

-d ctg x,

x 2 +1

d arctg x.

Таблицу дифференциалов необходимо знать наизусть.

7.7 Замена переменной

Теорема 45 (формула замены неременной). Если известно, что

j f(z)dz = F(z) + C,

то для любой дифференцируемой функции z

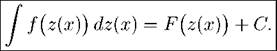
Иными словами, чтобы посчитать интеграл J f[z(x) dz(x), надо сна­чала посчитать интеграл J f(z) dz, а затем в ответ F(z) + C вместо z вписать z(x).

Доказательство. Действительно, неносредственно проверяется, что производная функции x i-^ F(z (x)) совпадает с функцией x i-^ f(z(x))z'(x)

П

Задача 44. Вычислите интеграл

----- dx.

x

Решение. Заметим, что в этом интеграле присутствует выражение —, имеющееся в таблице дифференциалов. Поэтому разумно нонробовать применить теорему 45:

/

ln x----- / dx i
----- dx = I ln^ x —= lln^xd(lnx) =
x x

(выполняем замену переменной)

₆ z ⁷

z = ln x >

z dz = + C 7

(возвращаемся к исходной переменной)

ln x C. ^

Подчеркнем, что, выполняя замену переменной, необходимо все вхо­ждения старой неременной заменить на новую неременную.

Прием из первой строки, состоящий в замене -^ на d(lnx) в соот­ветствии с таблицей дифференциалов, называют подведением под знак дифференциала.

Задача 45. Вычислите интеграл

f 5^

dx.

x

Решение. Заметим, что в этом интеграле присутствует множитель -^, который вместе с dx можно интерпретировать как дифференциал лx (с точностью до множителя), и в то же время оставшееся выражение является функцией л/x. Поэтому разумно нонробовать применить тео­рему 45:

x

5 x√ dx dx =

^√_x dx ^√_x √

5 √x = 5 2 d (x

5 ^√_xd (√x) =

(делаем замену переменной)

= Sw = л/ x } =2 [ 5 '^dw = 25 + C =

(возвращаемся к исходной неременной)

5^ 2 г

= 2—+ C = -5^ + C. П
ln5 ln5

7.8 Формула интегрирования но частям

Теорема 46 (формула интегрирования но частям). Пусть u иv —диф­ференцируемые функции. Тогда

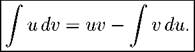
Доказательство. Достаточно взять интеграл от обеих частей равен­ства

u'v + uv'. П

(uv)

Наиболее часто формула интегрирования но частям применяется к интегралам следующих двух типов.

Первым типом неопределенных интегралов, берущихся по частям, называют интегралы вида

/ P(x) cos(kx + b) dx, / P(x) sin(kx + b) dx,

где P — многочлен.^^ Правило: применяя формулу интегрирования но частям к интегралам первого типа, надо через u обозначить P(x), а через dv — все остальное.

Вторым типом неопределенных интегралов, берущихся но частям, называют интегралы вида

/ P(x) arcs in (kx + b) dx, / P(x) arctg(kx + b) dx,

^^Напомним, что многочленом называют функцию вида P (х) = a о + a-^х + • • • + a^х^'

где P — многочлен. Правило: применяя формулу интегрирования но частям к интегралам второго тина, надо через u обозначить ln(kx + b), а через dv — P(x) dx.

К интегралам второго тина также относят интегралы вида

x ln ⁿ x dx.

Задача 46. Вычислите интеграл

5 xe ^{2 x- 3} dx

Решение. Этот интеграл относится к первому тину интегралов, беру­щихся но частям. Действуем в соответствии с правилом для интегралов первого тина:

5 xe ^{2 x- 3} dx

< udv>

u = 5 x,

du = u' dx = 5dx

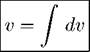
1 2 x 3 2

dv

2 x 3

dx,

J e^^x ^ dx = ie

<uv — vdu> = 5x-

2 x- 3

2 x- 3

5 dx

51 22

2 x 3

xe

2 4 Отметим еще одно правило: dunv всегда вычисляются но формулам

5 x 5

2 x- 3 2 x- 3

ee

dx

5 x

2 x- 3

2 x- 3

e + C

2 x 3

+ C.

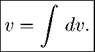
du = u' dx,

Задача 47. Вычислите интеграл

2 x

x ² e^x dx.

Решение. Этот интеграл относится к первому тину интегралов, беру­щихся по частям. Действуем в соответствии с правилом для интегралов первого тина:

^ udv>

= (u = x^, dv = e^x dx

\ du = 2x dx, v = J е_x dx = e

= {uv-Jvdu =

(u = x, dv = ex dx du = dx, v = J e x dx = e x

< = x^ex - 2 iuv - vduj =>

= x^ex -2{xex - exdx

= x^ex - 2xe^x + 2e^x + C. П Задача 48. Вычислите интеграл

Решение. Это интеграл второго тина.

l dx = Г u = ln x, dv = dx

du = _dx, v = J dx = x

- dx f

x — = x ln x - / dx

= xlnx - x + C. П

Задача 49. Вычислите интеграл

/ xln^xdx.

Решение. Этот интеграл похож на второй тип интегралов, берущихся но частям. Попробуем применить стандартное правило:

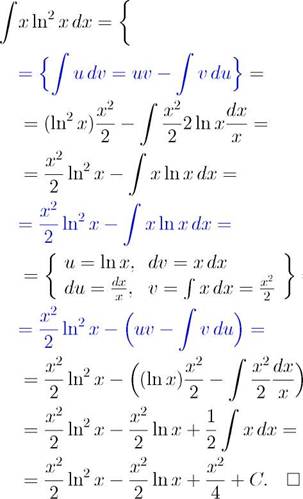u = ln x, dv = xdx 1

du = 2lnx^, v = Jxdx = Y

7.9 Как выбрать метод для вычисления интеграла

Полного алгоритма вычисления интегралов не существует. Тем не ме­нее, некоторые общие рекомендации возможны.

0. Универсальным правилом вычисления интеграла является только следующее: надо последовательно попробовать применить все 4 извест­ные метода (таблица интегралов, интегралы с линейным аргументом, замена переменной, формула интегрирования по частям).

1. Чтобы узнать, применима ли таблица интегралов, надо проверить, не совпадает ли интеграл дословно с одним из интегралов из таблицы.

2. Чтобы проверить, можно ли применить формулу интегрирования но частям, надо задать себе вопрос: пе относится ли данный интеграл к первому (содержит e^x) или второму (содержит ln x) типу интегралов, берущихся по частям.

3. Чтобы проверить, применимо ли правило вычисления интегралов с линейным аргументом, надо посмотреть, нет ли внутри интеграла функ­ций с линейным аргументом.

4. Чтобы проверить, можно ли применить правило замены неремен­ной, надо задать себе вопрос: нет ли в интеграле сомножителей, которые можно свернуть в дифференциал, используя таблицу дифференциалов.

7.10 Понятие о неберущихся интегралах

Напомним, что функции, которые можно задать аналитическим выра­жением, называют элементарными. В то же время произвольная функ­ция — это правило, нозволяюгцее по известному значению одной пере­менной вычислять значение другой. Далеко не все функции задаются аналитическими выражениями, т. е. являются элементарными.

Один из источников неэлементарных функций — операция взятия первообразной. Например, интегралы

f _ x 2 / о f dx f sinx

e dx, —, dx

lnx x

сугцествуют, но не выражаются через элементарные функции. Такие ин­тегралы называют неберущимися (в классе элементарных функций). Этот термин означает, что первообразную функции нельзя задать аналитиче­ским выражением, а не то, что первообразная не сугцествует.

Глава 8

Определенный интеграл

8.1 Определенный интеграл

как предел интегральных сумм

Пусть функция f определена на отрезке [ a, b]. Разобьем отрезок [ a, b] на части точками

τ: a = x ₀ < x1 < · · · < xn-1 < x_n = b.

Всякий такой набор точек называют разбиением отрезка. Здесь τ — со­кращенное имя разбиения.

y=f(x)

a= А ₀

Ж

x

^ ₃=b

Рис. 1: Разбиение отрезка

Отрезки [ xi- 1, xi]j на которые разрезается этими точками отрезок [ a, b] называют отрезками разбиения. Длины ∆xi = xi - xi-1 называют дли-

нами отрезков разбиения. А наибольшее из чисел ∆xi — диа.метро.м раз­биения. Диаметр разбиения τ обозначают символом \τ\:

\τ\ = max ∆xi.

i =1 ,...,n

	a=л0	i1	^	л3=b
		1 4	2 4

Рис. 2: Точки ξг

В каждом из отрезков разбиения выберем но точке ξi G [ xi _1 ,xi ].
Число

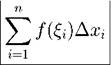
называют интегральной сум.мой. Подчеркнем, что оно зависит от функ­ции f, разбиения τ и выбора точек ξi.

Определенным, интегралом, от функции f но отрезку [ a, b] называют предел интегральных сумм, когда диаметр разбиения стремится к нулю:

b / f(x) dx = a

n i =1

Если этот предел существует (и конечен), функцию f называют инше-грируемой, а если не существует, — то неинтегрируемой.

Теорема 47. Если функция f иеирерывиа, то она интегрируема.

По определению считают, что

I f(x)dx = — / f(x)dx,

a

/ f(x) dx = 0 .

a

8.2 Геометрический смысл определенного интеграла

Гео.метрический смысл интегральной суммы заключается в том, что интегральная сумма представляет собой сумму площадей заштрихован­ных прямоугольников и тем самым приближает площадь фигуры, за-ключеппой между графиком функции f и осью X (в предположении, что f(x) > 0).

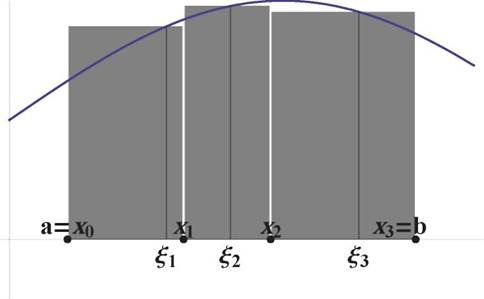
Рис. 3: Геометрический смысл интегральной суммы ^ n ^^ f (ξi)∆xi

При уменьшении диаметра разбиения объединение заштрихованных прямоугольников превращается в множество между графиком функции f и осью X. Отсюда

Геомет,рический смысл определенного инт,еграла: интеграл _a f(x) dx совпадает с площадью между графиком функции f и осью X (при усло­вии, что f(x) > 0).

Рис. 4: Геометрический смысл определенного интеграла

8.3 Производная интеграла с переменным верхним пределом

Теорема 48. Пусть функция f непрерывна на отрезке [ a, b ]. Тогда функ­ция

F(x) = _x f(t) dt

a

является первообразной функции f.

8.4 Формула Ньютона-Лейбница

Теорема 49 (формула Ньютона-Лейбница). Пусть функция F является первообразной непрерывной функции f. Тоща

b

f (x) dx = F (b) - F (a).

a

Теорема 49 является основным способом вычисления определенных интегралов. Ее можно рассматривать как второе определение онреде-ленного интеграла.

Принято следуюгцее сокращение:

F(b) - F(a) = F(x) 94

F (x)

Символ называют подстановкой. С помощью подстановки формулу Ньютон | -Лейбница записывают так:

b f(x) dx = a

F (x)

b a

Задача 50. Вычислите определенный интеграл

x ² dx.

Решение. Сначала обращаемся с интегралом как с неопределенным. Замечаем, что интеграл табличный. Вычисляем интеграл в соответствии с таблицей интегралов, только вместо константы пишем подстановку:

₂ x

x dx =
₂ 3

³ 3³

2 3 - 3 =63.

Задача 51. Вычислите определенные интегралы

e^x dx,

dx

x

Решение.

e^x dx = e^x

e -e

dx

x

ln x

ln e ln1=1 0=1.

8.5 Свойства определенного интеграла

Теорема 50. Определенный интеграл обладает следующими свойства­ми:

^{b b}

(a) / αf(x) dx = α J f(x) dx,

(b) / {f(x) ± g(x)) dx = J f(x) dx ± J g(x) dx,

b ^c b

(с) / f(x) dx = J f(x) dx + J f(x) dx.

a a c

Доказательство. Доказательства всех свойств основаны на исполь­зовании формулы Ньютона-Лейбница. Например, свойство (c) доказы­вается так:

F(b) - F(a) = (F (c) - F(a)) + {F(b) - F(c)).

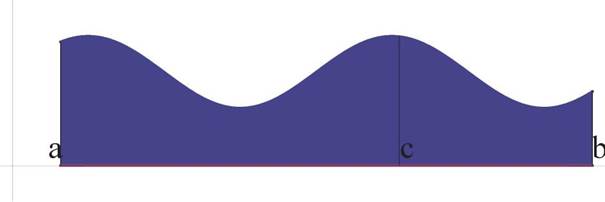
Рис. 5: Геометрический смысл равенства _a f(x) dx = _a f(x) dx + /^ f(x) dx

8.6 Замена переменной в определенном интеграле

Теорема 51. Пусть f — непрерывная функция, а z — непрерывно диф­ференцируемая функция}' Тогда

Г α

f[z(x)) dz(x)

a

f (z) dz.

В предноложенни, что

a = z(α), b = z (β).

(8л;

Задача 52. Вычислите определенный интеграл

³ e^{x 1}

x ²

dx.

^^Функцию называют непрерывно дифференцируемой, если ее ироизводиая существует и иенре-рывиа.

Решение. Начинаем со стандартной рекомендации: сначала можно об­ращаться с интегралом как с неопределенным, но при этом не терять пределы интегрирования. В соответствии с ней начинаем с обращения к таблице дифференциалов.

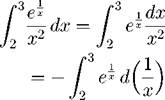
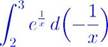
теперь выполняем замену переменной:

1 / 3 1 / 2

1 / 3

ez

1 / 3
1 _z

z = x = - 1 / 2 e dz =

1 / 3 1 / 2 1 / 2 1 / 3

(e e)= e e.

Правило: При замене неременных в онределенном интеграле надо не забывать менять пределы иитегрироваиия. После этого к старой пе­ременной возвращаться уже не надо.

Удобный для запоминания способ рассуждения такой. В старом ин­
теграле (т. е. до замены неременной) интегрирование велось но x, при
этом x менялся от 2 до 3. Новая переменная z связана со старой равен­
ством z = 1. Поэтому, когда x равняется 2, (то в силу равенства z = 1)
z равняется 1 / 2, а когда x равняется 3, z равняется 1 / 3. П

Задача 53. Вычислите определенный интеграл

dx.

0 \/4 + x

Решение. Начинаем со стандартной рекомендации: сначала можно об­ращаться с определенным интегралом как с неопределенным, но при этом не забывать переписывать пределы интегрирования.

Заметим, что аргументом корня является x ³ и в то же время присут­ствует множитель x ², который (с точностью до постоянного множителя) вместе с dx можно интерпретировать как дифференциал x ³. Поэтому разумно попробовать применить замену неременной:

0 \/4 + ж

x

dx

d (x 3

₀ √ 4+ x

₀ √ 4 + x ³ 3

3₀

\/4+

x ³

d (x ³

теперь выполняем замену переменной:

3 1 2 t = x = 3 0

dt

1 3 0

√ 4 + t

dt

л/ 4 + t

Обсудим замену пределов интегрирования. В старом интеграле (т. е. до замены переменной) интегрирование велось но ж, при этом х менялось от О до 2. Новая неременная t связана со старой равенством t = х ³.

x

t равняется

Значит, когда х равняется О, (то в силу равенства t

03, а когда х равняется 2, t равняется 23 = 8. Поэтому в качестве новых пределов иитегрироваиия записываем 0 и 8.

На этом решение примера пе закончилось. Далее замечаем, что полу­чился табличный интеграл с линейным аргументом. Поэтому

1 3

x

2 2 8

dt

0 √ 4+ x 3 1

√ 4 + t

2 √ 4 + t 3 2 √ √ 2 3(4+8 - 4+0)= 3 2 √ 4 √ (2 3 - 2)= (3 - 1)

dx

8.7 Формула интегрирования но частям для определенного интеграла

Теорема 52 (формула интегрирования но частям). Пусть и иу —непре­рывно дифференцируемые функции. Тогда

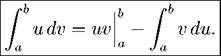
Задача 54. Найдите интеграл методом интегрирования по частям:

dx.

Г^ ln x Ji \[x

Решение. Этот интеграл относится ко второму типу интегралов, бе­рущихся по частям. Поэтому действуем в соответствии с правилом для второго типа интегралов:

dx

x dx √x

2 √x ln x

ln x

dx

u = ln x, dv

dx x,

x

du = ^dx, v =

\uv — v du

2л/ x

/ 2^/x —
l x

dx

22 x

2 √x ln x

2 √x ln x

- 2

теперь выполняем подстановки:

4л/ x

2 √x ln x

√√ (4 4 - 4 1)

√√ 2 4ln4 - 2 1ln1

4ln4 - 0 - (8 - 4)

8ln2 4.

8.8 Понятие о несобственных интегралах

Несобственными называют интегралы вида

+оо

oo +00

/ f(x) dx, I f(x)dx, f(x) dx.

Поскольку интегральные суммы для них не имеют смысла, несоб­ственные интегралы определяют с помощью равенств

/ f(x)dx= lim / f(x)dx,

/

b b

f(x)dx= lim / f(x)dx,
- oo a

+oo c +00

/ f(x)dx= / f(x)dx+ I f(x)dx,

где c G M произвольно.

Если эти пределы существуют, то говорят, что интегралы сходятся. Если пределы пе существуют, то говорят, что интегралы расходятся. В частности, интеграл считают расходящимся, если предел равен бесконеч­ности.

Рис. 6: a °° f(x) dx = lim a f(x) dx

Теорема 53. Интеграл

dx

α > 1

xα

СХОДИТСЯ тогда и только тогда, когда Задача 55. Какие из интегралов

∞ dx x 2

^{+ ∞} dx ₁ x

dx

x

сходятся

Следующая теорема играет иринципиальную роль в теории вероятно­стей.

Теорема 54 (интеграл Пуассона). Справедливо равенство

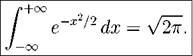
Задача 56. Вычислите интеграл

^∞ dx. x ²

Решение. Действуем согласно определению несобственного интеграла:

∞dx

lim ^ = lim — x b^+xJ1 x 2 b ^+оо\ x lim (-------) = lim (1 — - b ^+оо b 1 b ^+оо b

d

1.

Задача 57. Вычислите интеграл

^{+ ∞} dx. ₁ x

Решение. Действуем согласно определению:

dx ^b dx

lim ln x b→ + ∞

= lim x b→ + ∞ ₁ x

lim (ln b — ln 1)

lim (ln b — 0) = оо.

Таким образом, в ответ записываем, что этот интеграл расходится. П

Глава 9

Геометрические прилож:ения определенного интеграла

9.1 Вычисление площадей плоских фигур

Правило 1. Если f{x) > О, то площадь S между графиком функции f и осью X можно вычислить по формуле

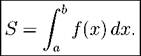
Рис. 1: Правило 1

Это свойство представляет собой геометрический смысл определенного интеграла.

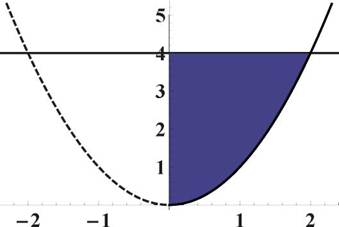
Задача 58. Найти площадь фигуры, ограниченной линиями x 0, y = 4.

y, x

Рис. 2: Задача 58

Решение. Искомая площадь S криволинейного треугольника OAB рав­на разности двух площадей: S = SOabc ~ SObc- Решая систему y = 4, x = л/ y, получаем, что точка B пересечения прямой y = 4 и кривой x = у/ y имеет координаты (2; 4).

x 3 3

2 3. Окончательно S

Тогда SOABC = 8, SObc = ₀ x2 dx

16 3 •

Правило 2. Если f(x) < 0, то площадь S между графиком функции f и осью X можно вычислить по формуле

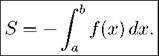
y=-f(x)

y=f(x)

Рис. 3: Обоснование правила 2

Отражая кривую y = f(x) относительно оси X, получаем кривую y = —f(x). Площадь иод этой кривой можно вычислить с помощью правила 1. Поэтому

S

f (x)) dx

или

S

f (x) dx.

Правило 3. Пусть f1(x) < f 2(x). Тогда площадь множества, заклю­ченного между кривыми y = f 2(x) а y = f ₁(x), вычисляется по формуле

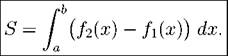
Рис. 4: Обоснование правила 3

Задача 59. Найти площадь фигуры, ограпичеппой линиями y

3x — ^.

y

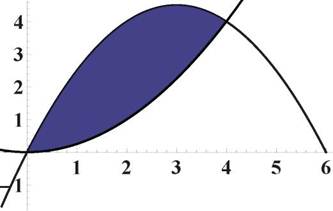
Рис. 5: Задача 59

3 x

Решение. Чтобы найти пределы интегрирования, найдем точки пере-

. Получаем

сечения парабол. Для этого решим уравнение ^ корпи xi = 0, x 2 = 4. Далее вычисляем площадь:

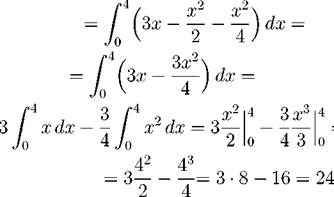
(f 2(x) - fi(x)) dx

S

16 = 8.

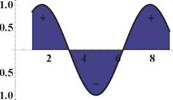
Правило 4. Если функция y = f(x) на отрезке [ a, b] меняет знак, то чтобы посчитать нлогцадь множества, заключенного между ее графиком и осью X, отрезок [ a, b] надо разбить па части так, чтобы па каждой из них функция y = f(x) была знакоиостоянна, а затем к каждой из частей применять правило 1 или 2.

Рис. 6: Правило 4

Правило 5. Если верхняя или нижняя граница множества состоит из графиков нескольких функций, то чтобы посчитать его илогцадь, мно­жество надо разрезать вертикальными линиями на несколько частей с тем, чтобы к каждой из них можно было применить одно из предыдущих правил.

Задача 60. Найти площадь фигуры, ограниченпой линиями y = x2 2-x,y = 0.

y

Решение. Точки пересечения очевидны. Разрезаем множество па две части вертикальной прямой x = 1. Вычисляем площади отдельных ча-

		/
		/
	4 3	/
	Ч 1	^^
-2	-1	24

Рис. 7: Задача 60: построение кривых

стеи:

5 ₁

5 ₂ S

x 2 d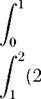x

x

x

x) dx = 2 x- 2

11 5 S ₁ + S ₂ = + = 32 6

9.2 Приближ:енное вычисление определенных интегралов

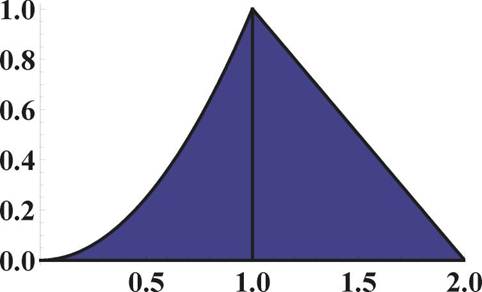
Пусть на отрезке [ a, b ] задана непрерывная функция y = f(x). Пред­положим донолнительно, что f(x) ≥ 0 на [ a, b]. Тогда _a f(x) dx числен­но равен площади под кривой y = f(x) на отрезке [ a, b ]. Мы получим приближенное значение искомого интеграла, если вместо площади под кривой возьмем площадь под ломаной, расположенной достаточно близ­ко к исходной кривой.

Для построения этой ломаной ностуним следующим образом: разо­бьем отрезок интегрирования на n равных частей длиной h = ^{b - a} и на каждом из отрезков разбиения [xi-1,xi], где i = 0,1 ,..., n, а xi = a + ih, заменим участок кривой y = f(x) секущей, стягивающей концевые точ­ки. Тогда

b

f (x) dx ≈ S ₁ + S ₂ + ··· + S_n,

a

где S 1, S 2 ,..., S_n — площади трапеций.

Рис. 8: Задача 60

h

Но S1

hf(x 0)+f(x 1). S ₂ = hf(x 1)+f(x 2)

f(x n- ₁ )+f(xn) „

---------------------. Поэтому

) Sn

b f (x) dx «h f (x ^)+ f (x 1) + h f (x ₁)+ f (x) +.. ^ + h f (xn - 1) + f (xn)

2 2 2

Приводя подобные члены и учитывая, что h = ^{b - a}, окончательно полу-

чаем

n

^b f(x)dx^b - a(f (x ₀) + f (x ₁ ) + --- + f (xn-1)+ f(x

n

где xi = a + ih, i = 0,1, 2 ,..., n.

a

Рис. 9: Приближенное вычисление определенных интегралов

S ₁

S ₃

Рис. 10: Построение ломаной

Глава 10

Дифференциальные уравнения

10.1 Основные определения

Дифференциальным, уравнением или подробнее обыкновенным диффе­ренциальным уравнением называют уравнение, неизвестным в котором является функция y = y (x). При этом в дифференциальное уравнение могут входить: аргумент функции x, значение y(x) неизвестной функции в точке x и значения y'(x)^..., y^ⁿ (x) нескольких ее производных.

Порядок старшей производной, входягцей в уравнение, называют по­рядком, дифференциального уравнения.

Пример 29. Примерами дифференциальных уравнений являются

y'(x)+y(x) = 0,

y' = y,

y'y = x.

Иногда дифференциальные уравнения первого порядка записывают в терминах дифференциалов^ а не производных, например,

f(x)gi(y) dx = f2(x)g2(y) dy.

Решением дифференциального уравнения называют такую функцию y = y (x), которая при подстановке ее в это уравпепие обращает его в верное равенство.

Процесс решения дифференциальных уравнений часто называют ин­тегрированием. дифференциальных уравнений.

Пример 30. Пепосредственно проверяется, что функция y = ex является решением дифференциального уравнения y'(x) = y (x) или в краткой

записи

y' = y.

Кроме того, решением того же уравнения является функция y = Ce^ при любом значении постоянной C.

Пример 31. Как известно, все решения дифферепциальпого уравпепия y'(x) = f(x) описьшаются формулой y = F(x) + C, где F — первообраз­ная функции f, а C — произвольная константа.

Примеры 30 и 31 показывают, что решений у дифференциального уравнения может быть много. Оказывается, так бывает всегда. Обыч­но множество всех решений удается описать одной формулой, содержа­щей параметры. Общим региением дифференциального уравнения n-го порядка называют функцию вида

n

y = ϕ(x,C1,...,C

которая содержит в себе все решения.

Часто сначала удается получить лишь соотношение вида

Φ(y,x,C 1 ,...,C,) = 0 ,

из которого, выражая y через все остальное, можно получить обгцее ре­шение. Такие соотношения называют общими интегралами.

В частности, обгцее решение уравпепия 1-го порядка имеет вид

y = ϕ(x,C),

а обгций интеграл —

Φ(y,x,C) = 0.

Частным решением дифференциального уравнения в противополож­ность общему решению называют любое конкретное решение. Так что частное решение и просто решение — синопимы.

Например, частное решение можно получить из общего решения, по­ставляя в него конкретные числовые зпачепия постоянных C 1, C 2 ,..., C ^.

10.2 Математическая модель

демографического процесса

Пусть: x — время

у (х) — количество населения в момент времени х;

ki у(х) — количество людей, рождающихся в единицу времени;

k2у(х) — количество, умирающих людей в единицу времени.

Тогда:

ki у(х)∆х — количество людей, рождающихся за время ∆х;

k2у(х)∆х — количество, умирающих людей за время ∆х.

Увеличение населения за время ∆х есть

у(х + ∆х) - у (х) = ki у(х)∆х - k2 у(х)∆х =

= (k - k2) • у (х)∆х = = kу(х)∆х,

где k = ki - k2. Окончательно получаем

у(х + ∆х) - у(х) = kу(х)∆х.

Разделив это равенство на ∆ж, получаем

у(х + ∆х) - у(х)
--------- ∆^--------- = k ^(") .

А переходя к пределу при ∆х -^ 0, приходим к дифференциальпому уравнению

у'(х) = kу(х)

10.Г

которое называют уравнением демографического роста. Мы увидим, что общее решение уравнения (10.1) имеет вид

у = Се''''.

10.3 Понятие о начальной задаче

Чтобы из общего решения дифференциального уравнения получить одно решение, добавляют дополнительные условия, которые называют начальными. Для уравнения первого порядка начальное условие выгля­дит так:

у(хо) = уо.

Начальной задачей называют нахождение решения, удовлетворяюще­го начальному условию.

Пример 32. Для уравнения

y (x) = ky(x)

примером начального условия является условие

y (0) = 10⁶.

Оно означает, что в начальный момент население составляло 106.

Чтобы найти решение, удовлетворяющее начальному условию, в об­щее решение

y = Ce''''

подставляют начальное условие y (x ₀ ) = y ₀. В нашем примере это приво­дит к следующему:

C= 10⁶,

y (x) = 106 e ^-" .

Для дифференциального уравнения второго порядка начальные усло­вия выглядят так:

y (x ₀ ) = y ₀, y ( x ₀ ) = y1.

в задачах механики (папомпим, что уравпепие Ньютона mr" = F явля­ется дифференциальным уравнением второго порядка) начальные усло­вия имеют смысл начальпого положения и начальной скорости.

10.4 Дифференциальные уравнения с разделяющимися переменными

Примером дифференциального уравнения с разделяющимися пере­менными является уравнение

y' = f(x)-g(y).

К уравнениям с разделяющимися неременными также относят уравне­ния, которые можно решить описываемым ниже методом разделения не­ременных. Например,

f ₁ (x)g ₁ (y) dx = f 2(x) g 2(y) dy. Метод разделения переменных заключается в следующем.

1. Производную y' записывают в виде ^:

2. Переменные разделяют^ т. е. все, что содержит y и dy, переносят в одну сторону, а все, что содержит x и dx, — в другую:

3. Берут неопределенные интегралы от обеих частей:

в результате вычисления получается соотношение вида

G(y) = F(x) + C,

представляющее собой общий интеграл.

4. Если можно, из этого соотношения y выражают через x и C и
получают общее peuieHue, которое записывают в ответ, а если не удается
выразить y через x и C, то в ответ записывают общий интеграл.

Задача 61. Найдите общее решение дифференциального уравнения

y' = xy. Решение. 1. Запишем производную y' в виде ^:

dy = x y.

dx

2. Разделим неременные, т. е. все, что содержит y и dy^ перенесем в одну сторону, а все, что содержит x и dx^ — в другую: