2014-02-24
3962
В ряде случаев при проектировании, а также при эксплуатации сетей небольшой сложности возникает необходимость проведения одноразовых расчетов без применения ПЭВМ, одним из распространенных способов ручного счета – последовательное упрощение схемы сложной сети по методу преобразования сети.
Сущность метода преобразования заключается в том, что заданную сложную сеть путем постепенных преобразований приводят к линии с двусторонним питанием, в которой распределение мощностей находят уже известным методом. Затем, после определения линейных мощностей на каждом участке преобразованной схемы, с помощью последовательных обратных преобразований находят действительное распределение мощностей в исходной схеме сети.
Эквивалентирование параллельных линии на любых участках замкнутой сети возможно только в том случае, если на этих линиях нет присоединенных нагрузок. Для участка замкнутой сети с двумя параллельными линиями (см.рисунок 4.9)
=
+
; 
.
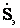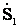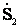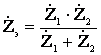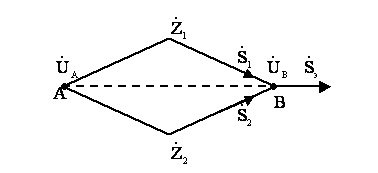
Рисунок 4.9
Если в схеме существуют промежуточные нагрузки, то эквивалентирование осуществить нельзя. Для этого делают так называемый перенос нагрузок в другие точки сети. При этом режим сети до переноса и после должен оставаться неизменным.
Вывод зависимостей, определяющих величины переменных нагрузок, можно сделать для общего случая, когда между точками сети, в которые требуется перенести нагрузку, имеется несколько потребителей энергии (см.рисунок 4.10).
Рисунок 4.10
Рассматривая сеть как линию с двусторонним питанием и принимая напряжения во всех узлах одинаковыми по величине и фазе в соответствии с (4.26), определим мощности, вытекающие из точек А и В
=
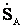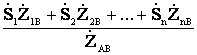, (4.32)
=
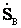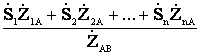. (4.33)
Если перенести нагрузку 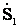в точки А и В, то схема участка сети примет вид (рисунок 4.10 б), а мощност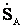и и 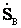определяются
=
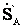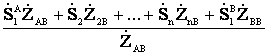, (4.34)
=
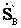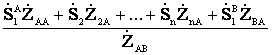(4.35)
где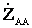 
=
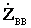=0.
Так как применение нагрузок не должно менять режима сети, находящейся за границами рассматриваемого участка, то 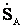= 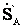и 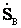=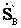. Приравнивая уравнения (4.32) и (4.34), а также (4.33) и (4.35), получим
=
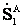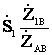и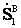 
=
.
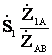Аналогично в общем случае для любой промежуточной нагрузки можно найти
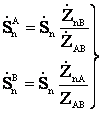(4.36)
Иногда при расчете сети требуется произвести преобразования треугольника в эквивалентную звезду и обратно (см.рисунок 4.11).
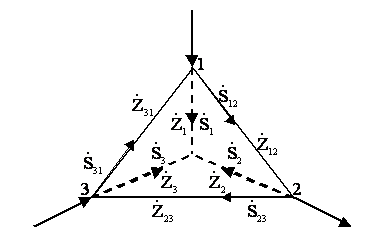
Рисунок 4.11
Сопротивления лучей эквивалентной звезды определяются
=
; 
=
; 
=
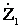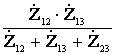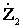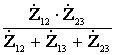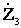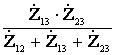. (4.37)
Обратные преобразования
(4.38)
При развертывании преобразований схемы в исходную необходимо найти распределение мощностей на сторонах треугольника по полученному распределению мощностей в лучах эквивалентной звезды.
Примем условно, что в лучах звезды получено распределение мощностей в соответствии с рисунком 4.11. Мощности на сторонах треугольника получаем, исходя из равенства векторов падений напряжения на любой стороне треугольника и смежных ей лучах звезды.
Задавшись направлениями мощностей на сторонах треугольника и определив токи на участках по номинальному напряжению сети, получим
,
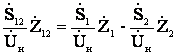откуда
(4.39)
Если результат получится с отрицательным знаком, то условно принятое направление мощности на этой стороне треугольника следует изменить на обратное.
