Цикл Карно, названный в честь французского инженера С. Карно, решает вопрос о максимальной доле теплоты, которая может превратиться в механическую энергию. Он состоит из двух адиабат и двух изотерм (рис.7.2), таким образом, являясь обратимым циклом
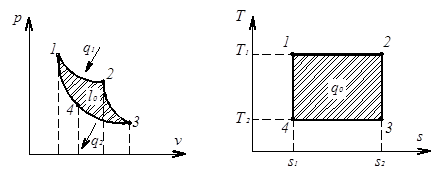
Рис. 7. Цикл Карно в координатах 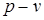 и
и 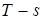
Рабочее тело массой 1 кг заключено в сосуд, стенки которого изолированы, чтобы была возможность совершать адиабатные процессы. Газ, имея начальные параметры 1, участвует в изотермическом процессе, который осуществляется при сообщении тепла q 1 от источника с температурой T 1. На 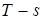 диаграмме эта теплота будет изображена площадью расположенной под линией 1 – 2 и будет найдена как
диаграмме эта теплота будет изображена площадью расположенной под линией 1 – 2 и будет найдена как
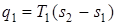 .
.
От точки 2 газ адиабатно расширяется до конечной точки 3. Полная работа расширения в 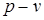 диаграмме измеряется площадью под линией 1 – 2 – 3. В
диаграмме измеряется площадью под линией 1 – 2 – 3. В 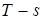 диаграмме адиабата расширения 2 – 3 пойдет вниз, так как температура рабочего тела снижается из-за уменьшения внутренней энергии, затрачиваемой на работу расширения газа.
диаграмме адиабата расширения 2 – 3 пойдет вниз, так как температура рабочего тела снижается из-за уменьшения внутренней энергии, затрачиваемой на работу расширения газа.
Из конечного состояния точки 3 рабочее тело можно вернуть в исходное состояние в точку 1, если его сжать. Карно предложил осуществить процесс сжатия по изотерме 3 – 4, при этом газ должен отдавать теплоту источнику с температурой T 2:
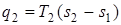 .
.
Конец изотермического сжатия выбирают так, чтобы газ, сжимаясь, вернулся бы в исходное состояние 1, но уже по адиабате 4 – 1. Суммарная работа, затрачиваемая на сжатие газа, в 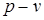 диаграмме измеряется площадью под линией 1 – 4 – 3.
диаграмме измеряется площадью под линией 1 – 4 – 3.
Полезная работа в цикле Карно изображается на 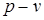 диаграмме площадью
диаграмме площадью 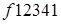 , а теплота, превращенная в работу, изображается на
, а теплота, превращенная в работу, изображается на 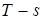 диаграмме –– площадью
диаграмме –– площадью  .
.
Термический к. п. д. для цикла Карно будет определяться
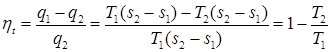 .
.
Отсюда следует:
1) к. п. д. цикла Карно зависит от температур источника теплоты и охладителя;
2) к. п. д. цикла Карно увеличивается при возрастании температуры T 1 источника теплоты и при уменьшении температуры T 2 охладителя;
3) к. п. д. цикла Карно всегда меньше 1, так как невозможно осуществить процесс, в котором 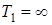 или
или 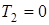 ;
;
4) к. п. д. цикла Карно при 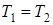 равен нулю, а значит невозможно превратить теплоту в работу, если все тела системы имеют одинаковую температуру.
равен нулю, а значит невозможно превратить теплоту в работу, если все тела системы имеют одинаковую температуру.
Характерная особенность цикла Карно состоит в том, что его к. п. д. не зависит от природы работающего тела, то есть при данных Т 1 и Т 2 он будет одинаков не только для идеальных, но и для реальных газов. Это положение известно как теорема Карно. Вместе с тем к. п. д. цикла Карно будет всегда больше к. п. д. любого другого цикла в тех же пределах температур, это доказывает, что цикл Карно является идеальным циклом. На практике же тепловые двигатели по нему не работают.
Если цикл Карно осуществлять в обратном направлении, то есть вести процессы расширения по адиабате и затем по изотерме с отбором теплоты от холодного источника, а процессы сжатия по адиабате и изотерме с отдачей горячему источнику, то на это потребуется затрата работы извне. Такой обратный цикл Карно является идеальным циклом для холодильных установок.
Для холодильных установок эффективность цикла, в котором полезным эффектом является теплота, отведенная от объектов охлаждения в холодильной камере q 2, будет оцениваться холодильным коэффициентом, который определяется:
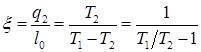 ,
,
где l 0 –– затраченная теплота в цикле.
Из полученного следует, что холодильный эффект может быть как больше, так и меньше единицы.
Для установок, в которых теплота q 1, отдаваемая высокотемпературной среде, является полезным эффектом, эффективность цикла будет оцениваться отопительным коэффициентом, рассчитываемым по формуле:
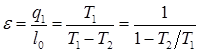 .
.
Так как температура горячего источника Т 1 всегда больше холодного источника Т 2, то отопительный коэффициент будет всегда больше единицы.
 2014-02-24
2014-02-24 1590
1590








