2014-02-24
2091
При перемещении газа с большой скоростью, пренебрегать изменением кинетической энергией движущихся масс нельзя, поэтому уравнения первого закона термодинамики и будут иметь другой вид.
Предположим, что по каналу переменного сечения под действием сил давления движется газовый поток. При этом будем считать:
1) движение газа по каналу установившееся и неразрывное. Это означает, что расход массы газа G в единицу времени будет постоянен для любого сечения и для любого момента времени:
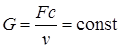, (2.85)
где F – площадь поперечного сечения канала, м2; с – скорость газа рассматриваемом сечении, м/с; v – удельный объем газа м3/кг;
2) скорости по сечению, перпендикулярному оси канала, постоянны. Это допущение равносильно тому, что в каждом сечении берется средняя по расходу скорость;
3) трением частиц газа друг о друга и о стенки канала пренебрегаем.
Очевидно, что количество подводимого тепла на участке между двумя произвольно выбранными будет расходоваться на изменение внутренней энергии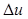 
, на совершение работы проталкивания 
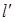и на приращение кинетической энергии газа 
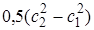при его перемещении:
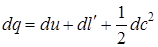. (2.86)
Работа проталкивания представляет собой разность
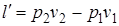или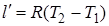 
. (2.87)
Располагаемая работа l 0, которую может произвести 1 кг движущегося газа над внешним объектом, можно найти:
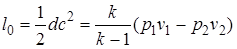. (2.88)
При адиабатном истечении первый закон термодинамики будет иметь вид: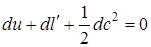 
, (2.89)
или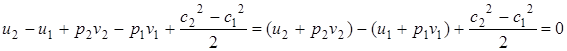 
;
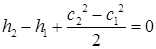. (2.90)
Тогда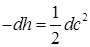 
, (2.91)
Таким образом, приращение кинетической энергии происходит за счет уменьшения его энтальпии.
Изменение энтальпии можно также найти, подставив в выражение значение располагаемой работы:
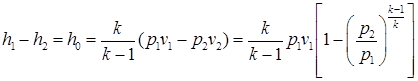. (2.92)
Исходными для определения скорости газового потока c при установившемся движении в произвольном сечении сопл и диффузоров являются уравнения (2.91) и (2.92) из которых следует:
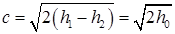, (2.93)
или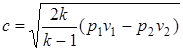 
, 
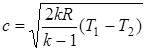, (2.94)
или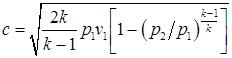 
, 
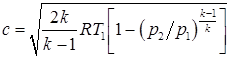. (2.95)
Массовый секундный расход газа при адиабатном стационарном течении с учетом, что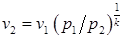 
, определяется:
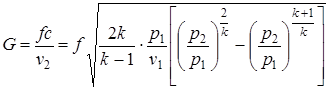. (2.96)
При определении скорости истечения и расхода прежде всего находят отношение (р 1/ р 2) и сравнивают его с так называемым критическим отношением, которое соответствует максимальному расходу газа в устье сопла, определяемым из равенства
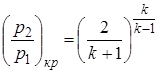. (2.97)
Если же адиабатное истечение газа происходит при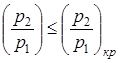 
, то теоретическая скорость газа в устье сопла будет равна критической скорости и определяться по уравнению
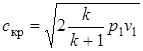или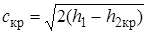 
(2.98)
Расход газа в этом случае будет максимальный и может быть вычислен по уравнению:
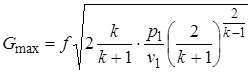. (2.99)
Для получения сверхзвуковых скоростей и паров в паровых и газовых турбинах применяют комбинированные сопла Лаваля (рис. 2.20).
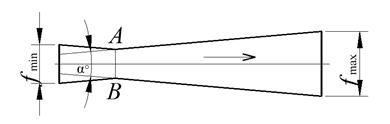
Рис.2.20. Сопло Лаваля
Первая часть сопла является суживающейся, вторая – расширяющейся. В этом случае первая часть сопла будет работать как дозвуковая, а вторая как сверхзвуковая и в горловине этих сопел (самом узком месте) будет устанавливаться скорость равная скорости звука, определяемая параметрами р кр, v кр.
Площадь минимального сечения сопла определяется по формуле
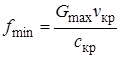. (2.100)
Площадь выходного сечения сопла
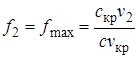, (2.101)
где v 2 – удельный расход газа при давлении среды р 2.
Длина расширяющейся части сопла определяется по уравнению
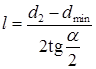, (2.102)
где d 2 и d min – соответственно диаметры выходного и минимального сечений, α – угол конусности расширяющейся части.
Действительная скорость истечения всегда меньше теоретической, так как процесс истечения связан с наличием трения. Если обозначить действительную скорость истечения через с д, то потеря кинетической энергии струи будет
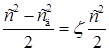, (2.103)
откуда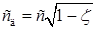 
. (2.104)
Обозначив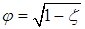 
, получаем 
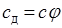. (2.105)
Коэффициент φ называют скоростным коэффициентом сопла, а коэффициент ζ – коэффициентом потери энергии.
Часть кинетической энергии в результате трения превращается в теплоту, которая при отсутствии теплообмена повышает энтальпию рабочего тела, вытекающего из сопла. Поэтому состояние газа или пара в конце действительного процесса истечения в h – s диаграмме изображается точкой, всегда расположенной правее точки, характеризующей состояние рабочего тела в идеальном процессе истечения.
