2014-02-24
457
Глава 4. Предельные переходы в неравенствах. Замечательные пределы.
Теорема. Если функция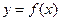 
неотрицательна в окрестности точки x 0, то и ее предел при x®x 0 тоже величине неотрицательная
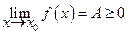. (3.9)
Доказательство ведем методом «от противного».
Предположим, что A < 0, т.е. – A > 0. В определении предела подразумевается, что в качестве ε можно выбрать любое положительное число. Возьмем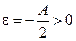 
, по нему найдем зависящее от e положительное число d(e) > 0 такое, что для всех х, удовлетворяющих неравенству ½ x0 - х ½< d, справедливо 
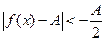. Раскроем модульное неравенство
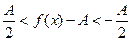
Рассмотрим правую часть неравенства и перенесем А направо. Получим
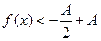
или
.
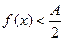Это означает, что функция 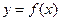отрицательна, что противоречит условию теоремы.
Следствие. Если f (x) < g (x), то и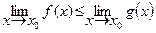
. (3.10)
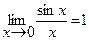. (3.11)
Построим тригонометрический круг с радиусом ОА = 1. Прямая DA – ось тангенсов. Возьмем на окружности точку В. Радиус ОВ = 1. Соединим точки А и В. Угол ВОА равен х, ВС = sin x, DA = tgx (рис. 4.1)
Предположим, что x > 0. Для x < 0 доказательство аналогично.,
Площадь треугольника ВОА
.
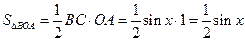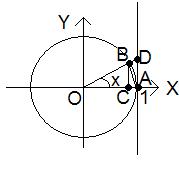
Рис. 4.1. Первый замечательный предел.
Площадь сектора ВОА
.
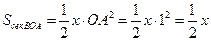Площадь треугольника DОА
.
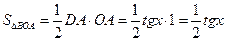Из чертежа следует, что для площадей выполняется соотношение
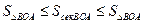
т.е.
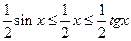
Сократим общий множитель ½ и разделим на sin (x). Получим
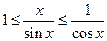
Или, для обратных величин
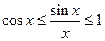
Так как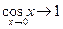 
, то и 
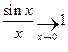. Что и требовалось доказать.
Следствие: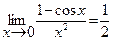 
(3.12)
