Решение. Так как 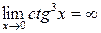 , а
, а 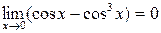 , то имеет место неопределенность вида
, то имеет место неопределенность вида 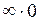 .
.
Выполним преобразования
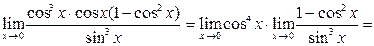
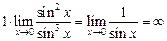 .
.
Пример 5. Вычислить 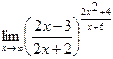 .
.
Решение. Так как 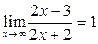 и
и 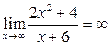 , то имеет место неопределенность вида
, то имеет место неопределенность вида 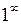 .
.
Возможны 2 способа решения примера.
1-й способ. Вспомним, что есть замечательный предел 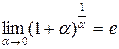 .
.
Используем этот замечательный предел, преобразовав исходный предел следующим образом:
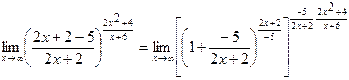 .
.
Имеем
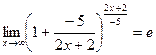 (здесь
(здесь 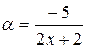 ),
),
и
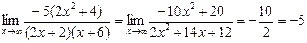 .
.
Таким образом,
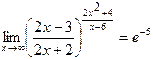 .
.
2-й способ.
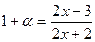
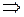
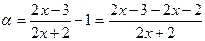 .
.
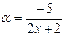 .
.
Причем 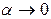 при
при 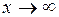 . Выразим
. Выразим 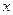 из равенства
из равенства
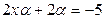 ;
; 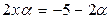 ;
; 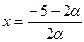 .
.
Таким образом,
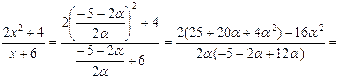
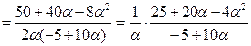 .
.
Выполним замену
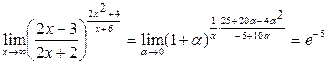 .
.
Так как
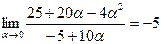 , а
, а 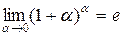 ,
,
то в итоге предел равен 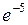 .
.
 2014-02-24
2014-02-24 469
469







