Глава 3. Теоремы о дифференцируемых функциях.
Глава 2. Связь между непрерывностью и дифференцируемостью. Дифференциал функции.
Теорема. Если функция у (x) = f (x) дифференцируема в своей области определения, то она непрерывна. Обратное не верно: из непрерывности функции дифференцируемость не следует.
Доказательство. Дифференцируемость означает наличие производной
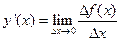 (2.1)
(2.1)
Используем теорему о разности между функцией и ее пределом (раздел 3. Формула (3.1)):
если
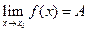 , (2.2)
, (2.2)
то
f (x) = A + a (х), (2.3)
где a (х) величина бесконечно малая.
Сравнивая выражения (2. 2) и (2. 3) получим, что в нашем случае
A 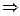 y’ (x), f (x)
y’ (x), f (x) 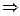
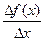 ,
, 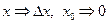
т.е.
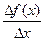 = y’ (x) + a (Δ х). (2.4)
= y’ (x) + a (Δ х). (2.4)
Умножим (2.4) на Δ х
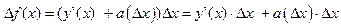 . (2.5)
. (2.5)
Из (2.5) следует, что если 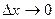 , то и
, то и 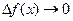 , что является доказательством непрерывности функции (см. раздел 3).
, что является доказательством непрерывности функции (см. раздел 3).
Приведем пример показывающий, что непрерывная функция может быть не дифференцируемой. Возьмем функцию
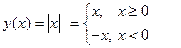
Эта функция непрерывна на всей области определения, так как в точке х 0 = 0 выполняется соотношение (см. раздел 3)
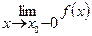 =
=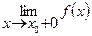 = f (x 0).
= f (x 0).
Действительно
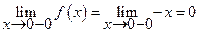
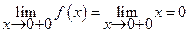 = f (x 0).
= f (x 0).
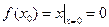
Следовательно в точке 0 функция непрерывна.
Но производной в этой точке нет, так как слева при x < 0, y ’(x) = -1, а справа при x > 0 y ’(x) = 1.
Вернемся к формуле (2.5). Дифференциалом df(x) функции f (x) в точке х называется линейная по D x часть приращения функции
d f (x) = 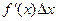 . (2.6)
. (2.6)
По определению для независимой переменной Δ х = d x. Поэтому дифференциал функции f(x) записывают чаще так
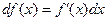 (2.7)
(2.7)
Формула (2.7) сохраняется и в том случае, когда х зависимая переменная (формула (2.6) для зависимой переменной неверна).
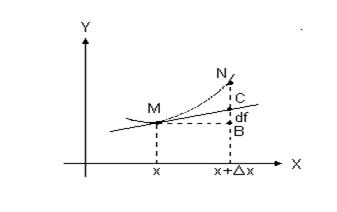
Геометрический смысл дифференциала (рис.2.1).
Производная f ¢(x) численно равна тангенсу угла наклона касательной к графику функции f (x). Дифференциал 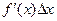 равен изменению ординаты, касательной к функции в точке N. Замена истинного приращения функции NB D f (x) = f (x + D x) - f (x) на дифференциал СВ
равен изменению ординаты, касательной к функции в точке N. Замена истинного приращения функции NB D f (x) = f (x + D x) - f (x) на дифференциал СВ 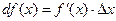 равносильна замене части графика функции на соответствующую часть касательной к этому графику (см. также рис.1.1).
равносильна замене части графика функции на соответствующую часть касательной к этому графику (см. также рис.1.1).

Производная f ¢(x) является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел отношения приращения производной к приращению аргумента
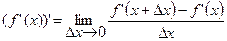 =
= 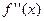 .
.
Если этот предел существует и конечен, то он называется второй производной от функции f(x) в точке х. Принятое обозначение:
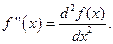
Подобным образом вводят производные n -го порядка f (n)(x) = (f (n-1)(x))¢.
В механике вторая производная от пути по времени есть ускорение
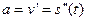
Пример 1. Производные от степенной функции y = х n.
y ¢ = n x n-1,
y ¢¢ = n (n-1) x n-2,
y ¢¢¢ = n (n-1) (n-2) x n-3,
...,
y(k) = n (n-1) (n-2)...(n-k+1) x (n-k) при (к £ n).
Пример 2. Точка совершает прямолинейное колебательное движение по закону 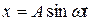 . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени 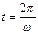 .
.
Решение. Найдем скорость 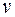 и ускорение а в любой момент времени t
и ускорение а в любой момент времени t
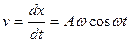 ;
; 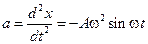 .
.
При 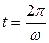
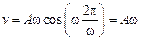 ,
, 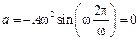 .
.
Дифференциалом второго порядка называется дифференциал от первого дифференциала
d(d f (x)) = (d f (x))¢Dx = (f ¢(x)D x)¢D x = f ¢¢(x) (D x)2
Пример. Вычислить производную функции заданной параметрически
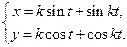
Функция 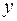 от независимой переменной
от независимой переменной 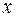 задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от 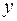 по
по 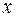 определяется формулой
определяется формулой
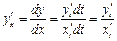
Находим производные от 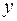 и
и 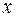 по параметру t:
по параметру t:
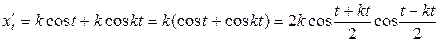 ,
,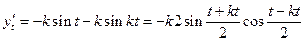 ,
,
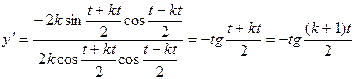 .
.
Для дифференцируемых функций выполняется ряд важных для приложений теорем. Перечислим основные теоремы.
Теорема Вейерштрасса.
Если функция непрерывна на замкнутом промежутке [a, b], то она достигает на этом промежутке наибольшего M и наименьшего m значений.
При этом могут возникать три случая.
1. Наименьшее и наибольшее значения достигаются внутра промежутка [a, b] (рис.3.1а).
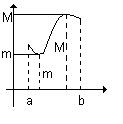
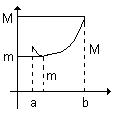
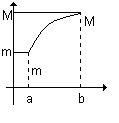
а б в
Рис. 3.1. Наибольшее и наименьшее значение функции на интервале.
2. На границе достигается либо только наибольшее, либо только наименьшее значение (рис. 3.1б).
3. На границе достигается и наибольшее и наименьшее значение (рис. 3.1в).
Пусть функция у = f (x):
1. непрерывна на отрезке [a, b],
2. дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b),
3. f (а) = f (b).
Тогда внутри отрезка (a, b) существует по крайней мере одна точка с a < c < b в которой производная обращается в ноль f `(c) = 0.
Замечание. Точка с является корнем производной. Если f(а) = f(b) =0, то теорема формулируется так: между корнями функции лежит корень производной.
Доказательство. Функция у = f (x) непрерывна на промежутке [a,b], то, по теореме Вейерштрасса, она достигает на нем своего наибольшего и наименьшего значений. Но так как значения функции на концах промежутка совпадают, то исключен третий случай теоремы Вейерштрасса, т.е. одно из значений – наибольшее или наименьшее – достигаются внутри промежутка. Предположим, что внутри в точке с a < c < b достигается наибольшее значение М = f (с), остальные случаи доказываются аналогично. Докажем, что в точке с производная обращается в ноль.
Возьмем два значения аргумента х 1 > c, х 2 < c (рис. 3.2).
Для х 1
D x = х 1 – с, D x > 0,
D f (x) = f (х 1) - f (с) = f (х 1) - М < 0.
Следовательно
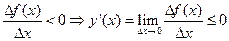
Для х 2
D x = х 2 – с, D x < 0,
D f (x) = f (х 2) - f (с) = f (х 2) - М < 0.
Следовательно
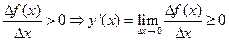
Тем самым, в точке с f `(c) = 0.
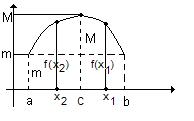
Рис. 3.2. Теорема Ролля.
Замечание. В точке с касательная идет горизонтально параллельно оси ОХ.
Формула Лагранжа (формула конечных приращений). Пусть функция у = f (x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b), то внутри отрезка существует по крайней мере одна точка с a < c < b в которой справедливо равенство: полное приращение функции равно производной, вычислленной в точке с, умноженной на длину промежутка
f (b) - f (а) = f `(c)(b - а). (3.1)
В точке с касательная параллельна секущей MN (см. рис. 3.3).
Теорема Коши. Пусть функции f (x) и g (x) непрерывны на отрезке [a,b], причем g (x) ≠ 0, дифференцируемы во всех внутренних точках отрезка, т. е. в интервале (a,b), то внутри отрезка существует точка с a < c < b в которой справедливо равенство
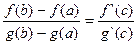 (3.2)
(3.2)
Правило Лопиталя. Пусть функции f (x) и g (x) на отрезке [a,b] удовлетворяют условию теоремы Коши и f (с) = g (с) = 0 (a < c < b), то если существует предел отношения производных при х →с, то существует и придел отношения функций в этой точке, причем
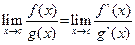 (3.3)
(3.3)
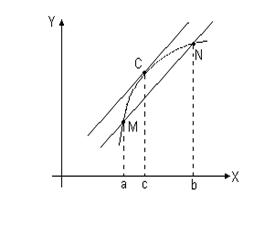
Замечание. Правило Лопиталя можно применять и для раскрытия неопределенностей типа 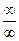 .
.
|
Пример. Вычислить предел 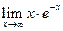 .
.
Решение. Так как е-х = 1/ех, то предел можно преобразовать к виду 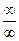
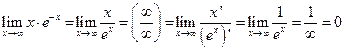 .
.
Формула Тейлора. Пусть функция у = f (x) в интервале (a,b) имеет производные до (n+1)-го порядка включительно. Приближающий полином n-ой степени, значение которого и его производных до порядка n включительно совпадают со значением функции и ее производных в точке x0 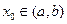 имеет вид
имеет вид
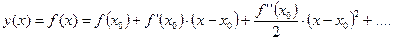
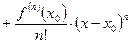 (3.4)
(3.4)
В окрестности точки х0 замена функции полиномом (3.4) дает некоторую ошибку. Формула Тейлораобеспечивает возможность точной замены данной функции полиномом
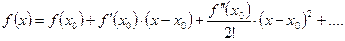
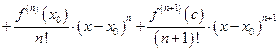 (3.5)
(3.5)
где a < x < b, a < x 0 < b, x 0 < c <x.
Выражение
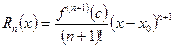 (3.6)
(3.6)
называется остаточным членом формулы Тейлора в форме Лагранжа. Величина Rn(x).определяет погрешность, возникающую при замене функции полиномом степени n из (3.4). Форма Лагранжа позволяет при вычислениях найти оценку сверху для ½Rn(x)½.
Если учесть, что
Δ х = х – х 0,
Δ f (x) = f (x) - f (x 0),
dn f (x)= f n(x)Δ х,
то получим дифференциальную форму формулы Тейлора
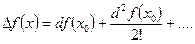
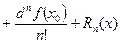 (3.7)
(3.7)
Формула Маклорена - частный случай формулы Тейлора, когда x 0 = 0.
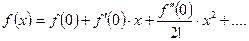
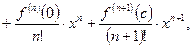 (3.8)
(3.8)
Пример. Вычислить значение числа е.
Решение. Построим формулу Тейлора для функции f (x) = ex в окрестности точки х0 = 0. Прежде всего, вычислим производные:
f (x) = ex, f ¢(x) = ex, f ¢¢(x) = ex,..., f (k)(x) = ex.
Отсюда
f (0) = f ¢(0) = f ¢¢(0) =... = f (k)(0) = 1.
Из (1.25) для f (x) = ex имеем
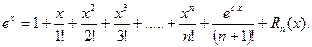
Эта формула получена для ex. Если в правой части положить х = 1, то
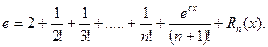
В зависимости от требований задачи эта формула позволяет получить сколь угодно точные значения величины e. Так
для n = 2 е» 2.5, ошибка не превышает величины 0.23,
для n = 3 е» 2.667, ошибка не превышает величины 0.052,
для n = 10 е» 2.7182818 и ошибка не более, чем 4.3 ּ 10-7.
 2014-02-24
2014-02-24 1666
1666